質問

これだけではよくわからないのですが、どちらがよりランダムなのでしょうか？

rand()

または :

rand() * rand()

私は本当に頭の体操になると思うのですが、手伝ってもらえますか？

EDITです。

直感的には、数学的な答えは「同じようにランダムである」ということになるのでしょうが、乱数アルゴリズム"を2回実行すると、2つを掛け合わせたときに、1回実行するよりもランダムなものができあがるのではないかと思わずにはいられません。

どのように解決するのですか？

説明

擬似ランダム変数やその乗算のランダム性を見抜こうとすると、必ず前の答えが正解になりますが、一方で、以下のことに注意する必要があります。 Random() は通常一様に分布しています。 Random() * Random() は、そうではありません。

例

これは 一様乱数分布のサンプル 擬似ランダム変数でシミュレートしています。

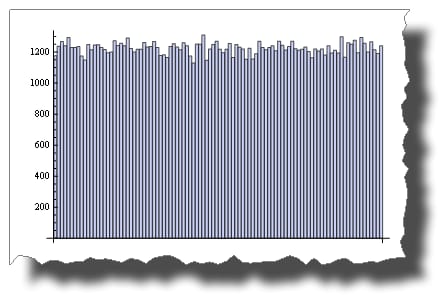
        BarChart[BinCounts[RandomReal[{0, 1}, 50000], 0.01]]

これは2つの確率変数を掛け合わせた後の分布ですが。

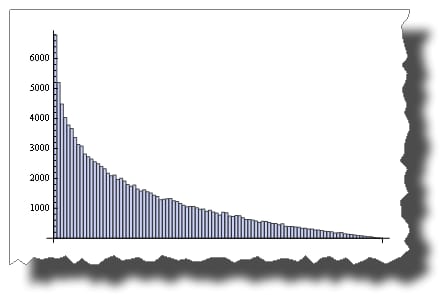
        BarChart[BinCounts[Table[RandomReal[{0, 1}, 50000] * 
                                 RandomReal[{0, 1}, 50000], {50000}], 0.01]]

つまり、どちらも「ランダム」なのですが、その分布は大きく異なっています。

もう一つの例

一方 2 * Random() は一様に分布する。

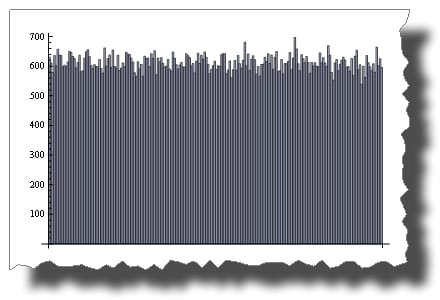
        BarChart[BinCounts[2 * RandomReal[{0, 1}, 50000], 0.01]]

Random() + Random() はNG!

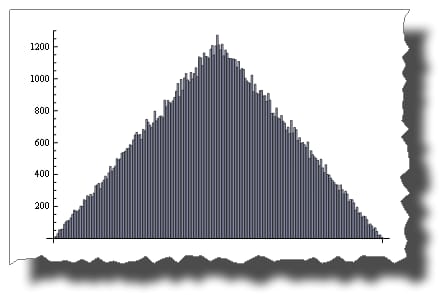
        BarChart[BinCounts[Table[RandomReal[{0, 1}, 50000] + 
                                 RandomReal[{0, 1}, 50000], {50000}], 0.01]]

中心極限定理（The Central Limit Theorem

その 中心極限定理 の和は ランダム() になる傾向があります。 正規分布 用語が増えるにつれて

たった4つの用語で、あなたは得をする。

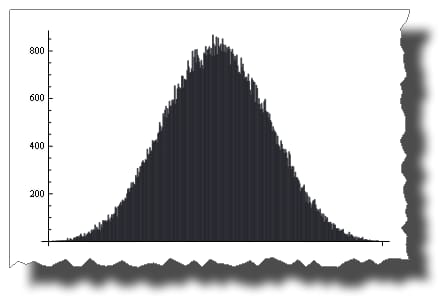
BarChart[BinCounts[Table[RandomReal[{0, 1}, 50000] + RandomReal[{0, 1}, 50000] +
                   Table[RandomReal[{0, 1}, 50000] + RandomReal[{0, 1}, 50000],
                   {50000}],
         0.01]]  

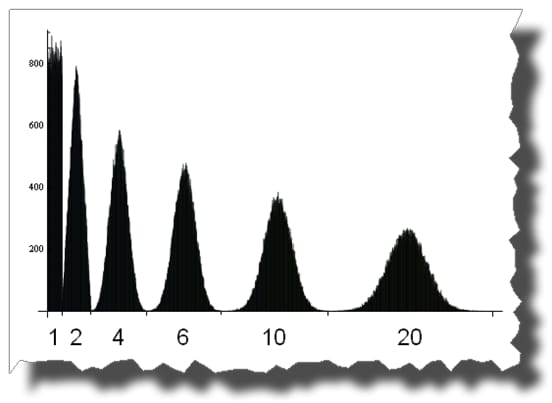
そして、ここでは、1、2、4、6、10、20の一様分布の確率変数を足し合わせることで、一様分布から正規分布への道を見ることができるのです。

編集

クレジットについて

感謝 トーマス・アーレ 最後の2つの画像に示されている確率分布は、「逐次比較型確率分布」として知られていることをコメントで指摘してくれた。 アーウィン-ホール分布

ありがとうございました 平家 素晴らしい トルン[]機能