[解決済み】「エントロピーと情報利得」って何？

質問

この本を読んでいます( NLTK ) で、混乱しています。 エントロピ は と定義されています。 :

エントロピーは、各ラベルの確率の和である。 その同じラベルの対数確率の倍

を適用するにはどうすればよいのでしょうか？ エントロピー と 最大エントロピー は、テキストマイニングの観点で？ どなたか簡単でシンプルな例（ビジュアル）を教えてください。

どのように解決するのですか？

エントロピーの話は、建築の文脈で出てきたのだと思いますが 決定木 .

説明のために、次のような作業を想像してみてください。 学習 を 分類 を男性/女性のグループに分ける。これは、名前のリストが与えられ、それぞれに m または f を学習させたい。 モデル は、データに適合し、新しい未知のファーストネームの性別を予測するために使用することができます。

name       gender
-----------------        Now we want to predict 
Ashley        f              the gender of "Amro" (my name)
Brian         m
Caroline      f
David         m

最初のステップは 決定 何 機能 は、予測したいターゲットクラスに関連するデータである。例えば、最初の文字/最後の文字、長さ、母音の数、母音で終わっているか、などです。つまり、特徴抽出後のデータは以下のようになります。

# name    ends-vowel  num-vowels   length   gender
# ------------------------------------------------
Ashley        1         3           6        f
Brian         0         2           5        m
Caroline      1         4           8        f
David         0         2           5        m

を構築することが目標です。 決定木 . の例です。 ツリー となります。

length<7
|   num-vowels<3: male
|   num-vowels>=3
|   |   ends-vowel=1: female
|   |   ends-vowel=0: male
length>=7
|   length=5: male

基本的に各ノードは1つの属性に対して行われたテストを表し、テストの結果に応じて左右に移動する。そして、クラス予測を含むリーフノードに到達するまで、ツリーを走査し続けます ( m または f )

そこで、名前を実行すると アムロ このツリーの下に、まず " をテストします。 は長さ<7? "であり、答えは はい ということで、その枝を下っていく。その枝に続いて、次のテスト " は母音の数<3? と評価されます。 真 . というラベルの付いたリーフノードにつながります。 m であり、したがって予測は 男性 (たまたま私がそうだったので、ツリーは結果を予測したのです。 正しく ).

決定木は トップダウン方式で構築される しかし、問題は、各ノードで分割する属性をどのように選択するかということです。答えは、ターゲットクラスをできるだけ純粋な子ノードに分割するのに最適な機能を見つけることです（つまり、男性と女性の両方を含むノードではなく、1つのクラスのみを含む純粋なノード）。

この指標は 純度 と呼ばれるものです。 情報 . を表します。 期待される の量 情報 は、そのノードに到達した例から、新しいインスタンス (first-name) を男性に分類すべきか女性に分類すべきかを指定するために必要であることがわかる。それを計算する は、そのノードの男性クラスと女性クラスの数に基づいている。

エントロピ 一方 不純物 (逆)です。について定義されています。 二値クラス 値を持つ a / b としています。

Entropy = - p(a)*log(p(a)) - p(b)*log(p(b))

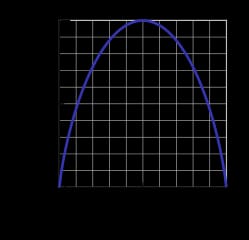
これは 2値エントロピー関数 は下図のように描かれている（確率変数は2つの値のいずれかを取る）。この図では、確率が p=1/2 という意味です。 p(X=a)=0.5 または同様に p(X=b)=0.5 のどちらかである確率が50％/50％である。 a または b (不確実性が最大となる）。エントロピー関数がゼロ最小になるのは、確率が p=1 または p=0 を完全確実なものにするため( p(X=a)=1 または p(X=a)=0 を意味し、後者は p(X=b)=1 ).

もちろん、エントロピーの定義は、（2つだけでなく）N個の結果を持つ離散確率変数Xに対して一般化することができます。

(その log を式で表すと、通常 2の底の対数 )

名前を分類する作業に戻り、例を挙げてみよう。ツリーを構成する過程のある時点で、次のような分岐を考えていたとする。

     ends-vowel
      [9m,5f]          <--- the [..,..] notation represents the class
    /          \            distribution of instances that reached a node
   =1          =0
 -------     -------
 [3m,4f]     [6m,1f]

ご覧の通り、分割前は男性9名、女性5名、つまり P(m)=9/14 と P(f)=5/14 . エントロピーの定義によると

Entropy_before = - (5/14)*log2(5/14) - (9/14)*log2(9/14) = 0.9403

次に、2つの子枝を見て、分岐を考慮した上で計算したエントロピーと比較します。の左の枝では ends-vowel=1 を、我々は持っている。

Entropy_left = - (3/7)*log2(3/7) - (4/7)*log2(4/7) = 0.9852

という右のブランチがあります。 ends-vowel=0 ということになります。

Entropy_right = - (6/7)*log2(6/7) - (1/7)*log2(1/7) = 0.5917

左右のエントロピーを、各枝のインスタンス数を用いて次のように結合する。 重み係数 (7インスタンスが左に、7インスタンスが右に)そして、分割後の最終的なエントロピーを求めます。

Entropy_after = 7/14*Entropy_left + 7/14*Entropy_right = 0.7885

ここで、分割前と分割後のエントロピーを比較することで、次のような指標が得られます。 情報利得 つまり、その機能を使って分割を行うことで、どれだけの情報を得ることができたか、ということです。

Information_Gain = Entropy_before - Entropy_after = 0.1518

上記の計算は、以下のように解釈できます。 end-vowels 機能を利用することで、サブツリー予測結果の不確実性を0.1518というわずかな量だけ減らすことができました（測定単位：百万円）。 ビット として 情報単位 ).

ツリーの各ノードで、すべての特徴量に対してこの計算が行われ、その中から 最大の情報量 での分割に選択されます。 欲張り を生成する機能を優先する）。 純粋 を、不確実性/エントロピーの低い分割を行う)。この処理は、ルートノードから下に再帰的に適用され、リーフノードがすべて同じクラスを持つインスタンスを含むときに停止する（それ以上分割する必要はない）。

をスキップしたことに注意してください。 詳細 をどのように処理するかなど、この記事の範囲外です。 数値機能 , 欠損値 , オーバーフィッティング そして プルーニング の木などです。