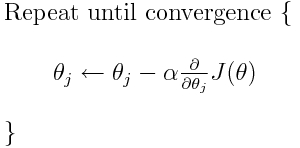[解決済み] クロスエントロピーとは?[クローズド]
質問
クロスエントロピーとは何か、いろいろな説明があるのは知っていますが、まだ混乱しています。
損失関数を記述するための手法に過ぎないのでしょうか?その損失関数を用いて勾配降下アルゴリズムで最小値を求めることはできるのでしょうか?
どのように解くのですか?
クロスエントロピーは、2つの確率分布の差を定量化するためによく使われます。機械学習の文脈では、カテゴリによるマルチクラス分類問題に対する誤差の尺度です。通常、真の分布 (機械学習アルゴリズムが一致させようとしている分布) は、ワンショット分布の用語で表現されます。
例えば、特定の学習インスタンスについて、真のラベルがB(可能なラベルA、B、Cのうち)であるとします。したがって、この学習インスタンスのワンショット分布は次のようになります。
Pr(Class A) Pr(Class B) Pr(Class C)
0.0 1.0 0.0
上記の真の分布は、学習インスタンスがクラスAである確率は0%、クラスBである確率は100%、クラスCである確率は0%であると解釈することができます。
さて、機械学習アルゴリズムが以下のような確率分布を予測したとします。
Pr(Class A) Pr(Class B) Pr(Class C)
0.228 0.619 0.153
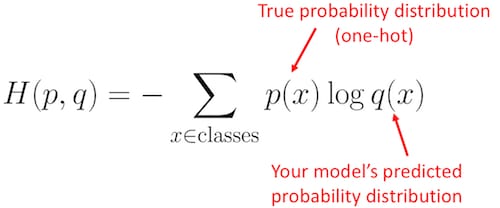
予測された分布がどれだけ真の分布に近いか。それはクロスエントロピーの損失が決定するものです。この式を使います。
ここで
p(x)
は真の確率分布(ワンショット)であり
q(x)
は予測された確率分布です。和は3つのクラスA,B,Cにわたります。この場合、損失は
0.479
:
H = - (0.0*ln(0.228) + 1.0*ln(0.619) + 0.0*ln(0.153)) = 0.479
対数の底
一貫して同じものを使っている限り、どの対数ベースを使っても問題ないことに注意してください。たまたま、PythonのNumpyの
log()
関数は自然対数(log base e)を計算します。
Pythonコード
上記の例をPythonでNumpyを使って表現してみます。
import numpy as np
p = np.array([0, 1, 0]) # True probability (one-hot)
q = np.array([0.228, 0.619, 0.153]) # Predicted probability
cross_entropy_loss = -np.sum(p * np.log(q))
print(cross_entropy_loss)
# 0.47965000629754095
つまり、あなたの予測が真の分布からどれくらい間違っているか、あるいはどれくらい離れているかを示しています。機械学習のオプティマイザーは損失を最小化しようとします (つまり、損失を 0.479 から 0.0 に減らそうとします)。
損失の単位
上記の例では、損失が0.4797であることがわかります。自然対数 (対数底 e) を使用しているので、単位は nats となるので、損失は 0.4797 nats となります。もし、logがlog base 2であれば、単位はビットとなります。参照 このページ を参照してください。
その他の例
これらの損失値が何を反映しているかをより直感的に理解するために、いくつかの極端な例を見てみましょう。
再び、真の(一発勝負の)分布があるとします。
Pr(Class A) Pr(Class B) Pr(Class C)
0.0 1.0 0.0
今、あなたの機械学習アルゴリズムが本当に素晴らしい仕事をし、非常に高い確率でクラスBを予測したとします。
Pr(Class A) Pr(Class B) Pr(Class C)
0.001 0.998 0.001
クロスエントロピーの損失を計算すると、損失はわずか0.002と小さいことがわかります。
p = np.array([0, 1, 0])
q = np.array([0.001, 0.998, 0.001])
print(-np.sum(p * np.log(q)))
# 0.0020020026706730793
もう一方の極端な例として,MLアルゴリズムがひどい仕事をし,代わりに高い確率でクラスCを予測したとします.その結果、6.91の損失はより大きな誤差を反映することになります。
Pr(Class A) Pr(Class B) Pr(Class C)
0.001 0.001 0.998
p = np.array([0, 1, 0])
q = np.array([0.001, 0.001, 0.998])
print(-np.sum(p * np.log(q)))
# 6.907755278982137
さて,この両極端の中間では何が起こるでしょうか?MLアルゴリズムが決まらず、3つのクラスをほぼ同じ確率で予測したとします。
Pr(Class A) Pr(Class B) Pr(Class C)
0.333 0.333 0.334
その結果、損失は1.10となります。
p = np.array([0, 1, 0])
q = np.array([0.333, 0.333, 0.334])
print(-np.sum(p * np.log(q)))
# 1.0996127890016931
勾配降下法へのフィッティング
クロスエントロピーは、多くの可能な損失関数のうちの1つです(もう1つの一般的なものはSVMヒンジ損失です)。これらの損失関数は通常 J(theta) と書かれ、勾配降下法 (パラメータ (または係数) を最適な値に近づけるための反復アルゴリズム) の中で使用することができます。以下の式では、以下のように置き換えることができます。
J(theta)
を
H(p, q)
. の導関数を計算する必要があることに注意してください。
H(p, q)
を最初に計算する必要があることに注意してください。
では、当初の質問に直接お答えします。
<ブロッククオート損失関数を記述する方法だけでしょうか?
正しくは、クロスエントロピーは2つの確率分布間の損失を記述するものです。多くの可能な損失関数の1つです。
そして、例えば勾配降下アルゴリズムを使って、最小値を見つけることができます。 を使うことができます。
はい、クロスエントロピーの損失関数は、勾配降下の一部として使用することができます。
さらに読む:私の 他の回答 TensorFlowに関連したものです。
関連
-
[解決済み] RuntimeError: 次元が範囲外([-1, 0]の範囲にあると期待されたが、1が得られた)
-
[解決済み] イプシロン貪欲q学習におけるイプシロンと学習率の減衰について
-
[解決済み] エアフローとKubeflowパイプラインの違いは何ですか?
-
[解決済み] コスト関数、線形回帰、シータをハードコーディングしないようにする。オクターブ
-
[解決済み] PyTorchのクロスエントロピー
-
[解決済み] kerasのtrain_on_batch()の使い道は?
-
[解決済み] ロジットとは何ですか?softmaxとsoftmax_cross_entropy_with_logitsの違いは何ですか?
-
[解決済み】同じ問題で binary_crossentropy と categorical_crossentropy が異なる性能を示すのはなぜか?
-
[解決済み] Appleはどのように電子メールの日付、時間、アドレスを見つけるのですか?
-
[解決済み] 期待値最大化手法の直感的な説明とは?[クローズド]
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
[解決済み】TensorFlowでtf.gradientsが動作する方法
-
[解決済み】Keras - KerasRegressorを使用して予測を実行する方法は?
-
[解決済み] Kerasにおける "Flatten "の役割とは?
-
[解決済み] RuntimeError: 次元が範囲外([-1, 0]の範囲にあると期待されたが、1が得られた)
-
[解決済み] ロジットとは何ですか?softmaxとsoftmax_cross_entropy_with_logitsの違いは何ですか?
-
[解決済み】線形回帰とロジスティック回帰の違いは何ですか?[クローズド]
-
[解決済み】データセットをトレーニングセットとバリデーションセットに分割する方法には法則性があるのでしょうか?[クローズド]
-
[解決済み] Diablo 2をプレイするための人工ニューラルネットワークを視覚的に学習させる方法とは?
-
[解決済み] 期待値最大化手法の直感的な説明とは?[クローズド]
-
[解決済み] なぜFメジャーはPrecisionとRecallの算術平均ではなく調和平均なのですか?