質問

Expectation Maximization (EM) は、データを分類する確率的手法の一種です。分類器ではないのであれば、間違っていたら訂正してください。

このEMの手法を直感的に説明するとどうなりますか？というのは expectation であり、何が maximized ?

どのように解決するのですか？

注：この回答の背後にあるコードは、見つけることができます。 ここで .

赤と青の2つの異なるグループからサンプリングされたデータがあるとします。

ここでは、どのデータポイントが赤と青のグループに属しているかがわかります。これにより、各グループを特徴付けるパラメータを簡単に見つけることができます。例えば、赤のグループの平均は約3、青のグループの平均は約7です（望めば正確な平均を求めることもできます）。

これは、一般的には 最尤推定 . あるデータが与えられたとき、そのデータを最もよく説明するパラメータ（1つまたは複数）の値を計算するのです。

ここで、私たちが はできません。 が見えないとします。私たちにはすべてが紫色に見えます。

ここで、私たちは に のグループがあるという知識はありますが、特定の値がどのグループに属するかはわかりません。

このデータに最も適合する赤のグループと青のグループの平均を推定することはできますか？

はい、しばしばできます! 期待値の最大化 は、それを行う方法を与えてくれます。このアルゴリズムの背後にある非常に一般的な考え方は、次のとおりです。

1. 各パラメーターがどのようなものであるかの初期推定値から開始します。
2. を計算します。 尤度 を計算する。
3. 各データポイントについて、パラメータによって生成される尤度に基づき、より赤かより青かを示す重みを計算する。その重みをデータ( 期待値 ).
4. 重み調整されたデータを使って、パラメータのより良い推定値を計算する ( 最大化 ).
5. パラメータ推定値が収束するまで（異なる推定値を出すのをやめるまで）、手順2～4を繰り返す。

これらのステップにはさらに説明が必要なので、上記の問題を通して説明します。

例：平均と標準偏差を推定する

この例ではPythonを使いますが、この言語に慣れていなくても、コードはかなり理解しやすいはずです。

赤と青の2つのグループがあり、値が上の画像のように分布しているとします。具体的には、各グループには 正規分布 から抽出された値が含まれており、そのパラメータは以下の通りです。

import numpy as np
from scipy import stats

np.random.seed(110) # for reproducible results

# set parameters
red_mean = 3
red_std = 0.8

blue_mean = 7
blue_std = 2

# draw 20 samples from normal distributions with red/blue parameters
red = np.random.normal(red_mean, red_std, size=20)
blue = np.random.normal(blue_mean, blue_std, size=20)

both_colours = np.sort(np.concatenate((red, blue))) # for later use...

ここでもう一度、この赤と青のグループの画像を見てみましょう（上にスクロールする手間を省くためです）。

各点の色（つまり、どのグループに属しているか）がわかると、各グループの平均と標準偏差を推定するのが非常に簡単になります。赤と青の値をNumPyの組み込み関数に渡すだけです。例えば

>>> np.mean(red)
2.802
>>> np.std(red)
0.871
>>> np.mean(blue)
6.932
>>> np.std(blue)
2.195

しかし、もし できない が見えないとしたらどうでしょう。つまり、赤や青ではなく、すべての点が紫に着色されているのです。

赤と青のグループの平均と標準偏差のパラメータを復元しようとすると、期待値最大化を使うことができます。

最初のステップ( ステップ1 は、各グループの平均と標準偏差のパラメータ値を推測することです。知的に推測する必要はなく、好きな数字を選べばよいのです。

# estimates for the mean
red_mean_guess = 1.1
blue_mean_guess = 9

# estimates for the standard deviation
red_std_guess = 2
blue_std_guess = 1.7

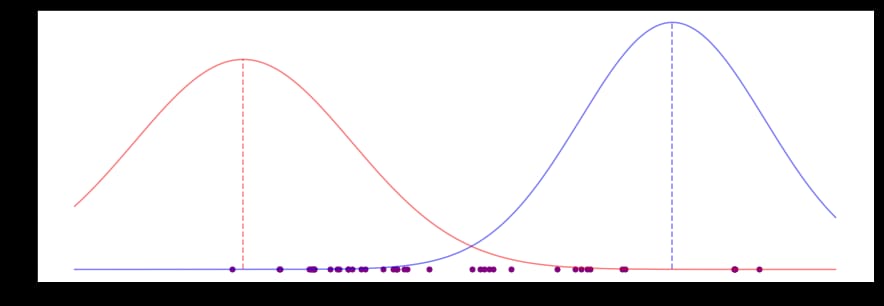
これらのパラメータ推定値は、次のようなベルカーブを生成します。

これらは悪い推定値です。両方の平均 (垂直の点線) は、たとえば、ポイントの賢明なグループのための任意の種類の "middle" から大きく外れているように見えます。私たちはこれらの推定値を改善したいと思います。

次のステップ( ステップ2 )は、現在のパラメータ推測の下で現れる各データ点の尤度を計算することです。

likelihood_of_red = stats.norm(red_mean_guess, red_std_guess).pdf(both_colours)
likelihood_of_blue = stats.norm(blue_mean_guess, blue_std_guess).pdf(both_colours)

ここでは、各データポイントを単純に 確率密度関数 に置き換えるだけです。赤と青の平均と標準偏差の現在の推測を使用しています。これにより、例えば、現在の推測では、1.761のデータポイントは次のようになります。 非常に 青 (0.00003) よりも赤 (0.189) である可能性がより高いことがわかります。

各データポイントについて、この2つの尤度の値を重みに変換することができます ( ステップ3 )に変換して、以下のように和が1になるようにします。

likelihood_total = likelihood_of_red + likelihood_of_blue

red_weight = likelihood_of_red / likelihood_total
blue_weight = likelihood_of_blue / likelihood_total

現在の推定値と新しく計算した重みを用いて 新しい を計算することができます。 ステップ4 ).

を用いて平均と標準偏差を2回計算します。 すべて を用いて、赤の重みと青の重みで2回平均と標準偏差を計算します。

直感の重要な部分は、データポイントの色の重みが大きければ大きいほど、そのデータポイントはその色のパラメータの次の推定値に影響を与えるということです。これは、パラメータを正しい方向に引っ張る効果があります。

def estimate_mean(data, weight):
    """
    For each data point, multiply the point by the probability it
    was drawn from the colour's distribution (its "weight").

    Divide by the total weight: essentially, we're finding where 
    the weight is centred among our data points.
    """
    return np.sum(data * weight) / np.sum(weight)

def estimate_std(data, weight, mean):
    """
    For each data point, multiply the point's squared difference
    from a mean value by the probability it was drawn from
    that distribution (its "weight").

    Divide by the total weight: essentially, we're finding where 
    the weight is centred among the values for the difference of
    each data point from the mean.

    This is the estimate of the variance, take the positive square
    root to find the standard deviation.
    """
    variance = np.sum(weight * (data - mean)**2) / np.sum(weight)
    return np.sqrt(variance)

# new estimates for standard deviation
blue_std_guess = estimate_std(both_colours, blue_weight, blue_mean_guess)
red_std_guess = estimate_std(both_colours, red_weight, red_mean_guess)

# new estimates for mean
red_mean_guess = estimate_mean(both_colours, red_weight)
blue_mean_guess = estimate_mean(both_colours, blue_weight)

パラメータの新しい推定値が得られました。これを再び改善するために、ステップ2に戻り、この処理を繰り返します。推定値が収束するまで、あるいはある程度の回数の繰り返しが行われるまでこれを行います ( ステップ5 ).

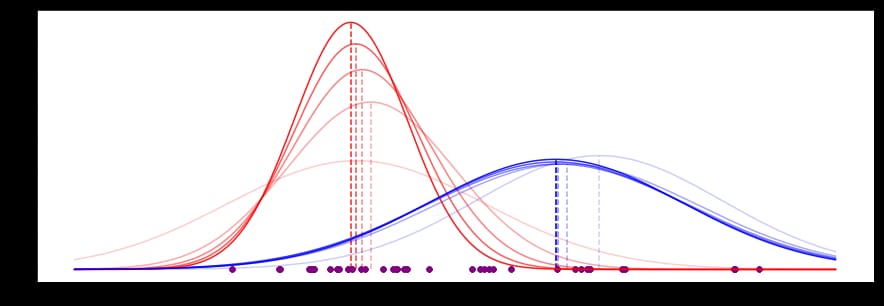
私たちのデータでは、このプロセスの最初の5つの反復は次のようになります（最近の反復は外観が強くなっています）。

平均値はすでにある値に収束しており、曲線の形状（標準偏差に支配されている）も安定してきていることがわかります。

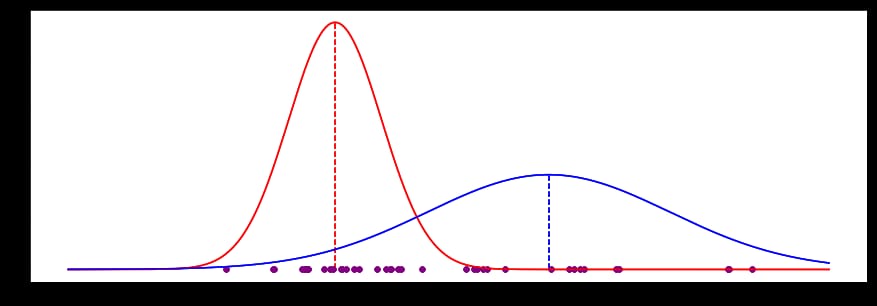
20回繰り返すと、次のようになります。

EMプロセスは以下の値に収束し、実際の値に非常に近いことがわかりました（色が見えるところ、隠れた変数がないところ）。

          | EM guess | Actual |  Delta
----------+----------+--------+-------
Red mean  |    2.910 |  2.802 |  0.108
Red std   |    0.854 |  0.871 | -0.017
Blue mean |    6.838 |  6.932 | -0.094
Blue std  |    2.227 |  2.195 |  0.032

上記のコードで、標準偏差の新しい推定値が平均の前の推定値を使用して計算されたことに気づかれたかもしれません。最終的には、ある中心点の周りの値の（加重）分散を見つけるだけなので、最初に平均の新しい値を計算しても問題ではありません。パラメータの推定値が収束していくのがわかります。