[解決済み】線形回帰とロジスティック回帰の違いは何ですか？[クローズド］

質問

の値を予測する必要がある場合 カテゴリカル (または離散) の結果を使用します。 ロジスティック回帰 . 私は、以下のように考えています。 線形回帰 を使えば、入力値から結果の値を予測することもできます。

では、この2つの方法論の違いは何でしょうか。

どのように解決するのか？

• 確率としての線形回帰の出力

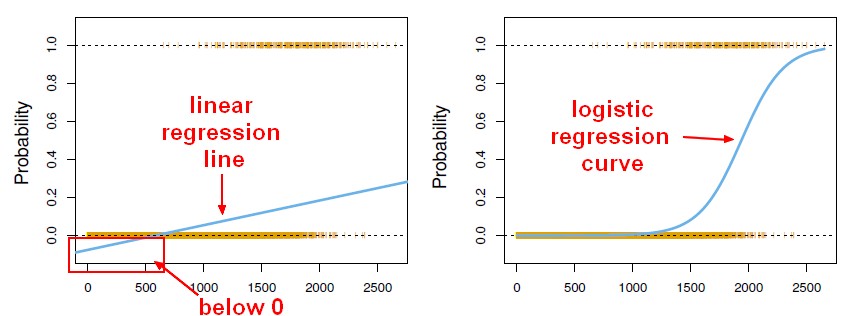
  線形回帰の出力を確率として使いたくなりますが、それは間違いです。なぜなら、出力は負になったり、1より大きくなったりすることがありますが、確率はそうならないからです。回帰は、実際には 0より小さい確率、あるいは0より大きい確率を生み出す可能性があります。 1となり、ロジスティック回帰が導入された。

  出典 http://gerardnico.com/wiki/data_mining/simple_logistic_regression

  

• 成果

  線形回帰では，結果（従属変数）は連続的である． それは無限の可能な値のうちのどれかを持つことができる．

  ロジスティック回帰では、結果（従属変数）は限られた数の可能な値しか持ちません。

• 従属変数

  ロジスティック回帰は、応答変数がカテゴリカルである場合に使用されます。たとえば，yes/no, true/false, red/green/blue, 1位/2位/3位/4位、など。

  線形回帰は、応答変数が連続的である場合に使用されます。例えば、体重、身長、時間数などです。

• 方程式

  線形回帰は、Y = mX + Cのような方程式を与えます。 は次数1の方程式を意味する。

  しかし、ロジスティック回帰では、次のような式が得られます。 Y = e ^X + e ^-X

• 係数の解釈

  線形回帰では、独立変数の係数の解釈は非常に簡単です（すなわち、他のすべての変数を一定に保ち、この変数の単位増加で、従属変数はxxxだけ増加/減少すると期待されます）。

  しかし、ロジスティック回帰の場合、系列（二項、ポアソン。 など）、リンク（log、logit、inverse-logなど）を使用すると、解釈が違ってきます。

• 誤差を最小化する技術

  線形回帰は 通常の最小二乗法 を最小化する方法です。 というのは、ロジスティック回帰の場合は、その誤差を最小限に抑えるため は 最尤法 という手法で解を求めます。

  線形回帰は通常、データに対するモデルの最小二乗誤差を最小化することによって解かれるため、大きな誤差は二次的にペナルティが課されます。

  ロジスティック回帰はまさにその逆です。ロジスティック損失関数を用いると、大きな誤差は漸近的に定数になるようにペナルティが課される。

  なぜこれが問題なのかを知るために、カテゴリ{0, 1}の結果に対する線形回帰を考えてみましょう。もし、あなたのモデルが結果を38と予測し、真実は1であった場合、あなたは何も失うことはありません。線形回帰はその38を減らそうとしますが、ロジスティック回帰はそうしません（それほどではありませんが）。 ² .