ロジスティック回帰は2分法モデル

ロジスティック回帰、別名log-odds regression（この名前の由来は後述します）。まず、これは分類モデルであって、回帰モデルではないことを強調しましょう 以下では、ロジスティック回帰の原理をさまざまな方法で説明した後、ロジスティック回帰のアルゴリズムを、勾配上昇アルゴリズムと確率的勾配上昇アルゴリズムを使ってそれぞれ例に当てはめてみます。

---

I. ロジスティック回帰と線形回帰の関係

前々から気になっていたのですが、ロジスティック回帰は名前に "regression" が入っているので、回帰モデルとは全く関係ないのでしょうか？はい、関係があります！以下でそれについてお話します。

まず線形回帰モデルが与えられます。 

というベクトル形式で書かれる。 

また、"一般化線形回帰"モデルとは。 

ここで、g(〜)は単調微分可能な関数であることに注意してください。

ここで、次に線形回帰の回帰モデルからロジスティック回帰の分類モデルへとつながるのです!!!!

線形回帰モデルの魅力は回帰学習しかできないことはわかったが、分類タスクをどうやるか！？その答えは、一般化線形回帰モデルにあります：分類タスクの真のマーカーyを線形回帰モデルの予測値に関係付ける単調微分可能な関数を見つけるだけです!

ロジスティック回帰はバイナリ問題を扱うので、出力トークンy={0,1}、線形回帰モデルからの予測値z=wx+bは実数値なので、実数zを0/1の値に変換すればよく、そのオプション関数が"ユニットステップ関数"になります。 

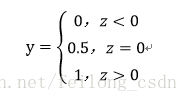
このような予測は、0より大きければ正、0より小さければ負、0に等しければ任意と判断されるのです

しかし、ユニットステップ関数は非連続関数であるため、連続関数が必要であり、"Sigmoid function"がユニットステップ関数の良い代替となります。

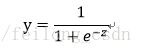
シグモイド関数は単調微分可能でありながら単位ステップ関数をある程度近似しており、そのイメージは以下のようになります。 

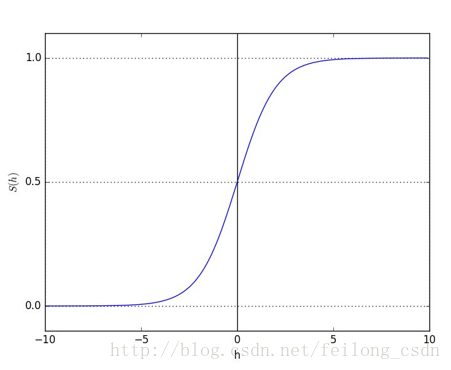
このように、元の線形回帰モデルにシグモイド関数をかけて、ロジスティック回帰モデルの予測関数を形成し、二項対立の問題で使用することができるのです。

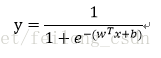
上式の予測関数の変換は 

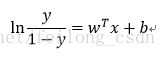
上の式を見ると、サンプルxが陽性例である確率をyとすると、1-yは陰性例である確率であることがわかります。この2つの比は、オッズ比と呼ばれ、xが陽性の例である相対的な可能性を反映します。

ここで、線形回帰モデルとロジスティック回帰の関係もまとめておきましょう。 
ロジスティック回帰分類モデルの予測関数は、真のマーカーの対数オッズを線形回帰モデルの予測値で近似しています! これはまた、線形回帰の予測値と分類タスクの真のマーカーとの間の上述のリンクを可能にします!

次に、勾配上昇アルゴリズムにより、ロジスティック回帰モデルのパラメータw

前回のトピックでは、ロジスティック回帰の予測関数を得ました。 

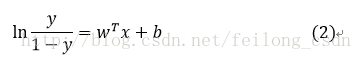
ここで、式中のyをクラス事後確率推定値p(y=1|x)と考えると、上式は以下のように書き換えることができる。 

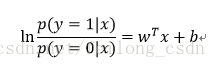
上の式を解くと、次のようになる。 

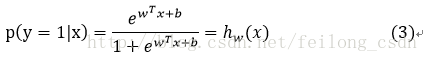
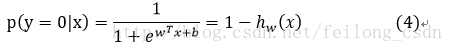
パラメータwを解くという考え方が先にあり、その考え方に沿ってパラメータwを解いていきます。 
1. パラメータwを解くために、基準関数J(w)を定義し、その基準関数を用いてパラメータwを解く必要がある 
2. 最尤推定法により基準関数J(w)を定義する。 
3. 次に、基準関数J(w)を最大化することで、パラメータwの反復式を求めることができる。 
4. パラメータwを求めるためのデータをより有効に活用するために、第3ステップで得られたwの反復をベクトル化します。これでパラメータwの導出作業は完了です！次は例の応用です。

ステップ1：基準関数J(w)を解く

2つの式(3)(4)を組み合わせると、次のようになる。 

式(5)のy={0,1}は、二項対立の問題なので、yは0か1の2つの値をとるだけです。 
(5)式によれば、尤度関数は次のようになる。 

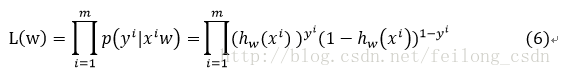
式(6)の対数をとると、次のようになる。 

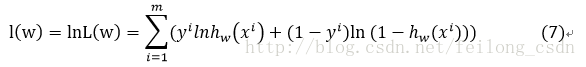
したがって、基準関数は次のように定義される。 

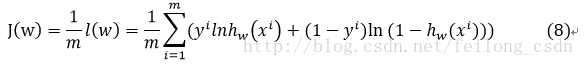
最終的には、最大化基準関数である尤度関数を最大化することが目標である。 

---

ステップ2：勾配上昇アルゴリズムがパラメータwを解く

ここでは、勾配上昇アルゴリズムを使ってパラメータwを解くので、パラメータwの反復式は次のようになる。 

ここで、αは正のスケーリングファクターで、ステップの学習率を設定します。 
ここで、基準関数J(w)を微分すると、次のようになる。 

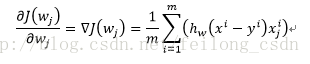
そこで、最終的なパラメータwの反復計算式は次のように求められる。 

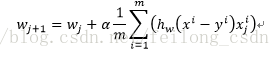
上記の式は、(1/m)を削除しても結果に影響はなく、以下の式と等価である。 

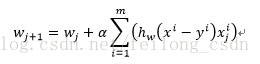
ここまでで、wの反復式にたどり着きましたが、これは定義上、データの導入でwの計算が可能になり、その結果、分類が可能になるのだそうです しかし、データは基本的に行列とベクトルで導入されるので、例のアプリケーションで使いやすいように、wを反復する際に上記をベクトル化する必要があります。

---

ステップ3：wの反復計算式をベクトル化する

まず導入されたデータセットxについて、両者を以下のように行列として導入する。 

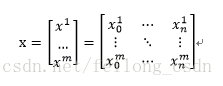
ここで、mはデータの数、nはデータの次元数、すなわちデータの特徴量の数です

ここでも、ラベルyはベクトルとして導入される。 

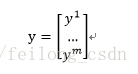
パラメータwは、次のようにベクトル化されます。 

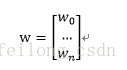
ここでM=x*wを定義しておくので。 

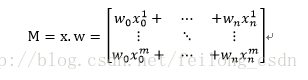
上記のシグモイド関数を次のように定義する。 

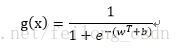
そこで、推定誤差損失を次のように定義する。 

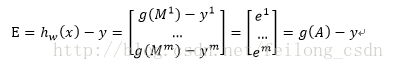
これをもとに、ステップ2で求めたパラメータ反復時のベクトル化の式を次のように求めることができる。 

これでパラメータwの反復計算式の導出は完了です！次の例で応用して、実用的な分析ができるようになります。ロジスティック回帰アルゴリズムを用いた簡単な2値分類問題の例です!

---

III. ロジスティック回帰アルゴリズム(pyhton)の適用例

これは、2次元空間に2種類のデータ点が与えられた例で、あとは2種類のデータに対する分類関数を求め、学習させた新しいモデルに対して、新しいデータを入力すれば、そのデータが2次元空間の2種類のデータのどちらに属するかを判断することができますね

Pythonで実装したサンプルコードのデモを行う前に、基準関数を最適化するための2つの方法について説明します。 
1. 勾配上昇アルゴリズム 
2、ランダム勾配上昇アルゴリズム

勾配上昇アルゴリズム。 
勾配降下法は、私たちが普段使っている勾配降下法と考え方が似ています。勾配上昇アルゴリズムは、ある関数の最大値を見つけるには、その関数の勾配方向に沿って探索するのが最も良い方法であるという考えに基づいています。停止条件に達するまで 
勾配上昇アルゴリズムのシュードコード。 

Stochastic gradient ascent アルゴリズム。 
勾配上昇アルゴリズムでは、回帰係数が更新されるたびにデータセット全体をトラバースする必要があり、小規模なデータでは問題ないが、数十億のサンプルと数千の特徴量では計算が複雑になりすぎる。確率的勾配上昇アルゴリズムは，新しいサンプルが入ってきたときに分類器を段階的に更新できるため，オンライン学習アルゴリズムと言えます．そして，gradient ascent アルゴリズムはバッチアルゴリズムです．

改良型確率的勾配上昇アルゴリズム。 
確率的勾配上昇アルゴリズムでは計算量が大幅に削減されるが、同時に正答率も低下する! そこで、stochastic gradient ascent アルゴリズムは改良することができる! その改良は2つの分野に分けられる。 
1つ目の改良点は、学習率αを非線形降下法で毎回異なるようにすることです 
改善点2：一度に1つのデータを使用するが、毎回ランダムにデータを選択し、選択されたものは選択しないようにする。

これらの情報を踏まえて、サンプルコードに詳細なコメントをつけてご紹介します。

#! /usr/bin/env python3

# -*- coding: utf-8 -*-


from numpy import *

import matplotlib.pyplot as plt


# load data from file: feature X, label label

def loadDataSet():

dataMatrix=[]

dataLabel=[]

# Here's an easy way to read a file in python

f=open('testSet.txt')

for line in f.readlines():

#print(line)

lineList=line.strip().split()

dataMatrix.append([1,float(lineList[0]),float(lineList[1])])

dataLabel.append(int(lineList[2]))

#for i in range(len(dataMatrix)):

# print(dataMatrix[i])

#print(dataLabel)

# print(mat(dataLabel).transpose())

matLabel=mat(dataLabel).transpose()

return dataMatrix,matLabel


#logistic regression uses the sigmoid function

def sigmoid(inX):

return 1/(1+exp(-inX))


#The function involves the operation of how to transform a list into a matrix: mat()

# Also contains the transpose operation for matrices: transpose()

#There are also list and array shape functions

#When dealing with matrix multiplication, it is important to pay attention to whether the dimensions correspond to each other


#graAscent function implements the gradient ascent method, which implies complex mathematical reasoning

#gradient ascent algorithm, each parameter iteration needs to traverse the entire data set

def graAscent(dataMatrix,matLabel):

m,n=shape(dataMatrix)

matMatrix=mat(dataMatrix)


w=ones((n,1))

alpha=0.001

num=500

for i in range(num):

error=sigmoid(matMatrix*w)-matLabel

w=w-alpha*matMatrix.transpose()*error

return w



# implementation of stochastic gradient ascent algorithm, for the case of more data less computational effort, but poor classification effect

# each parameter iteration through a data operation

def stocGraAscent(dataMatrix,matLabel):

m,n=shape(dataMatrix)

matMatrix=mat(dataMatrix)


w=ones((n,1))

alpha=0.001

num=20 # here the number of iterations for the classification effect has a great impact, very small classification effect is very poor

for i in range(num):

for j in range(m):

error=sigmoid(matMatrix[j]*w)-matLabel[j]

w=w-alpha*matMatrix[j].transpose()*error

return w


#Improved stochastic gradient ascent algorithm

#Improved the stochastic gradient ascent algorithm from two aspects, the correct rate really improved a lot

#Improvement one: for the learning rate alpha using non-linear descent way to make each time is different

#Improvement 2: use one data at a time, but select the data randomly each time, and do not select the selected data again

def stocGraAscent1(dataMatrix,matLabel):

m,n=shape(dataMatrix)

matMatrix=mat(dataMatrix)


w=ones((n,1))

num=200 # here the number of iterations for the classification effect has a great impact, very small classification effect is very poor

setIndex=set([])

for i in range(num):

for j in range(m):

alpha=4/(1+i+j)+0.01


dataIndex=random.randint(0,100)

while dataIndex in setIndex:

setIndex.add(dataIndex)

dataIndex=random.randint(0,100)

error=sigmoid(matMatrix[dataIndex]*w)-matLabel[dataIndex]

w=w-alpha*matMatrix[dataIndex].transpose()*error

return w


# Draw the image

def draw(weight):

x0List=[];y0List=[];

x1List=[];y1List=[];

f=open('testSet.txt','r')

for line in f.readlines():

lineList=line.strip().split()

if lineList[2]=='0':

x0List.append(float(lineList[0]))

y0List.append(float(lineList[1]))

else:

x1List.append(float(lineList[0]))

y1List.append(float(lineList[1]))


fig=plt.figure()

ax=fig.add_subplot(111)

ax.scatter(x0List,y0List,s=10,c='red')

ax.scatter(x1List,y1List,s=10,c='green')


xList=[];yList=[]

x=arange(-3,3,0.1)

for i in arange(len(x)):

xLis

上記のプログラムを実行すると、次のような結果が得られます。 

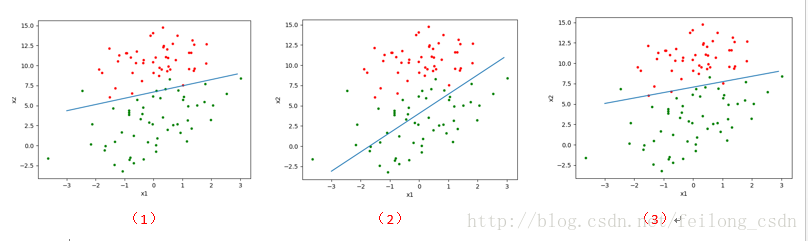
どこで 
図(1)は、演算量の多い勾配上昇アルゴリズムを使用した場合の結果である。 
図(2)は確率的勾配上昇アルゴリズムを用いた結果であり、分類結果が若干悪く、運用の複雑さは低い。 
図(3)は、改良された確率的勾配上昇アルゴリズムを使用したもので、良好な分類と低い計算量が得られています。

上記プログラムのデータ接続で、パスワード：1l1sを抽出したところ

もし、文章に問題があれば、遠慮なく訂正してください！ありがとうございます。

参考文献

https://blog.csdn.net/feilong_csdn/article/details/64128443