ターゲット検出ベースモジュール(iou/giou/ciou/diou)のIoU概要
1 はじめに
IoUは、交差比率やマージ比率とも呼ばれ、異なる画像が互いに重なり合う割合を計算するアルゴリズムであり、深層学習ではターゲット検出や意味分割のタスクによく利用される。
1.1 IoUのターゲット検出への応用
ターゲット検出タスクでは、モデルに大量のバウンドボックス候補を一度に生成させ、各ボックスの信頼度に従ってソートし、ボックス間のIoUを順に非最大抑制的に計算し、どれが探している真のオブジェクトでどれを除去すべきかを決定することがよくあります。例えば、顔検出を行う場合、モデルの出力は左の画像で、最終的に得られるのは右の画像になることがあります。


また、最終的な出力を得た後、出力ボックスと元のマーカーボックスの間のIoU(ground truth bound)を取り、1-IoUを損失として(最小値を見つけるための区間[0,1])、それを使ってモデルの反復最適化を実現することができます。

モデル出力ボックス(黄色)とIoUを計算するための実顔ボックス(赤色)の組み合わせ
![]()
1.2 セマンティックセグメンテーションにおけるIoU
セマンティックセグメンテーションのタスクでは、画像中の予測領域と実領域のIoUを計算し、1-IoUをLossとして、モデルを繰り返し最適化することも可能である。


左の肖像画をモデルでキーアウトすると、右の赤い部分が実際の肖像画の領域、黄色い部分がモデルの予測値になります
![]()
1.3 IoUの最終目標
以上の例から、IoUの計算は、大きさ、面積、位置が異なる2つのフレームや2つの画像を比較することと捉えることができ、ひいては2つの画像間の幾何学的類似性を比較することと考えることができますので、この類似性に関わるパラメータは何か考えてみましょう。重なり具合、グラフの距離、形状の類似性(矩形の縦横比)などが考えられる。
以下、IoUの計算の仕組みと、理想に向かって段階的に最適化されていく様子を説明します。
2 IoU
2.1 IoUの原則
IoUとは、Intersection over Unionの略で、「交差と連合の比率」としても知られている。ioUは、ターゲット検出とセマンティックセグメンテーションの両方で重要な役割を果たす。
まず、IoUの定義から説明します。
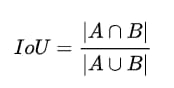
直感的には、IoUの値を2つのグラフの面積の交点とそれらの和の比率として設定すれば、以下のようになる。
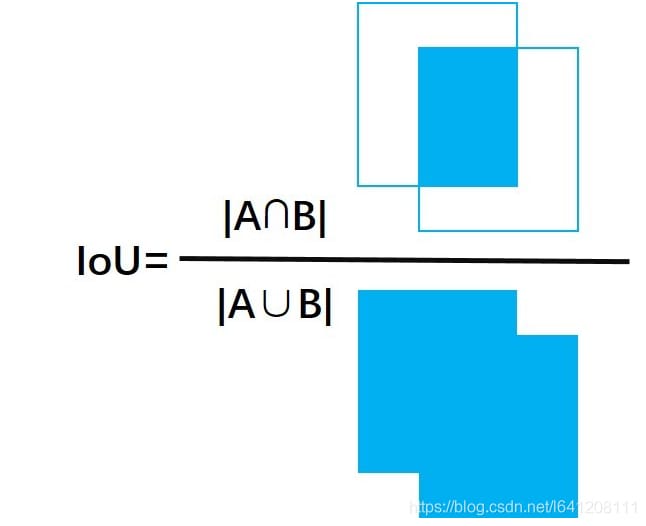
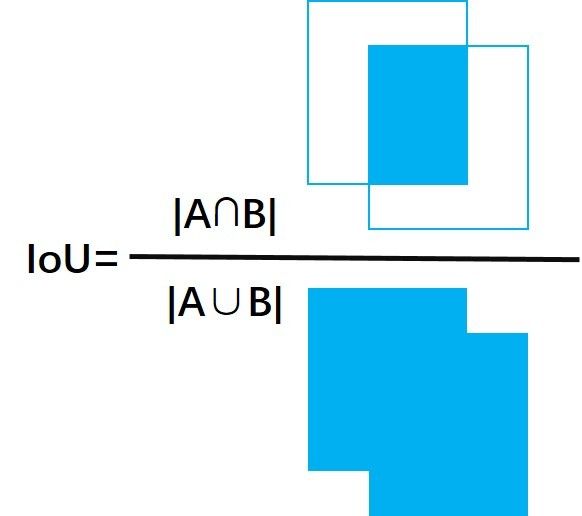
IoUで2枚の画像の重なりを判断することには、いくつかの利点があります。
- スケール不変であること。
- 非負荷性を満たす。
- 対称性を満たす。
しかし一方で、IoUには非常にわかりやすい欠点がいくつかあります。
- A∩B|=0の場合、つまり2つの画像が交差していない場合、2つの画像間の距離を比較することができないこと。
- 2つの画像がどのように正確に交差しているかを表現することができない。
このIoUは、当初、2つの画像の幾何学的な類似性を計算するという要件を満たし、画像の重なりの計算を単純に実装しているが、2つの図形間の距離や図形の縦横比の類似性を反映することができないと推測される。
2.2 IoUの計算
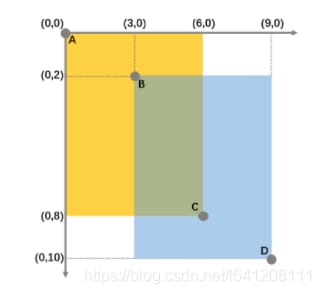
それでは、IoUの手動計算を説明します。

2.3 IoUの実装
import numpy as np
# box:[up, left, down, right]
box1 = [0,0,8,6]
box2 = [2,3,10,9]
def IoU(box1, box2):
# Calculate the width and height of the middle rectangle
in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
# Calculate intersection, concatenation area
inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
(box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
# Calculate IoU
iou = inter / union
return iou
IoU(box1, box2)
アウト:0.23076923076923078
3 GIoU
3.1 GIoUの原則
GIoU (Generalized Intersection over Union) は IoU に比べて「一般化」しており、IoU をより一般化したレベルで計算することができ、先ほどの「2つの画像が交差していない場合、2つの画像の距離を比較することができない」という問題を解決することができます。
GIoUは次のように計算される。
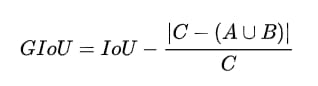
ここで、Cは2つの画像の最小包絡線面積を表し、2つの画像の最小外郭の面積と解釈することも可能である。
これより、次のことがわかります。
- 元のIoUは値域[0,1]をとり、GIoUは値域[-1,1]をとる。二つの画像が完全に重なるときIoU=GIoU=1、二つの画像が無限に離れているときIoU=0、GIoU=-1である。
-
重なり合う領域のみに着目するIoUとは異なり、GIoUは重なり合う領域だけでなく、重なり合わない領域にも着目するため、2つの画像の重なりをよりよく反映させることができるのです。
この時点で、GIoUは画像の重なりの計算を改善したが、まだグラフの距離やアスペクト比の類似性をうまく表現できていないと考えることができる。
注)GIoU論文アドレス https://arxiv.org/pdf/1902.09630.pdf
3.2 GIoUの算出
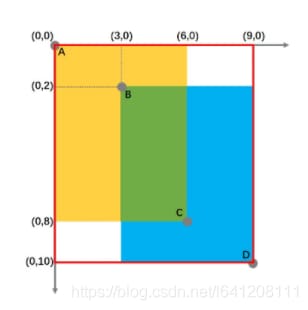

3.3 GIoUの実装
import numpy as np
# box:[up, left, down, right]
box1 = [0,0,8,6]
box2 = [2,3,10,9]
def GIoU(box1, box2):
# Calculate the minimum envelope area
y1,x1,y2,x2 = box1
y3,x3,y4,x4 = box2
area_C = (max(x1,x2,x3,x4) - min(x1,x2,x3,x4)) * \
(max(y1,y2,y3,y4) - min(y1,y2,y3,y4))
# Calculate IoU
in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
(box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
iou = inter / union
# Calculate the percentage of blank parts
end_area = (area_C - union)/area_C
giou = iou - end_area
return giou
GIoU(box1, box2)
アウト:0.09743589743589745
4 DIoU
4.1 DIoUの原則
GIoUはIoUの問題点をいくつか解決しているが,予測フレームとターゲットフレーム間の距離を直接反映したものではない。この問題を解決できるのが,2つのフレームの重なり,距離,スケールを考慮したDIoU(Distance-IoU)であり,DIoUは以下のように算出される。
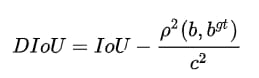
ここで、b, bgt はそれぞれ二つの箱の中心を表し、ρは二つの中心間のユークリッド距離、Cは最小包絡矩形の対角線、すなわち下図のようになる。
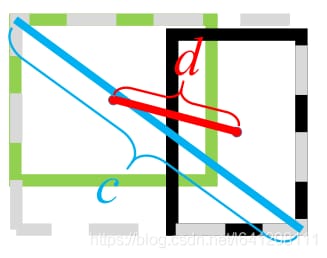
DIoUが他の2つの計算方法と比較して優れている点は、以下の通りです。
- DIoUは2つのボックス間の距離を直接最小化するため、損失関数として使用すると収束が早くなります。
- 2つの箱が上下、左右に完全に並んでいる場合、GIoUはIoUにほぼ縮退するが、DIoUはまだ有効であるため、空白部分は存在しない。
この時点で、DIoUは画像の重なりの計算を洗練させた上で、グラフィカルな距離の考察を実現していると考えることができますが、それでもグラフィカルなアスペクト比の類似性をうまく表現できているとは言えません。
注)DIoU論文アドレス https://arxiv.org/pdf/1911.08287.pdf
4.3 DIoUの計算
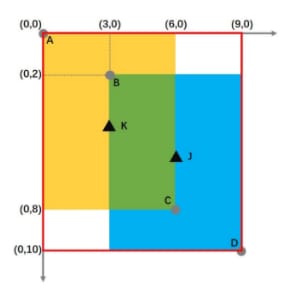
黄色い箱の中心点Kと青い箱の中心点Jの座標は、次のように計算できます。
K: (3,4) J: (6,6)
すると、この時点でのDIoUの計算結果は次のようになります。
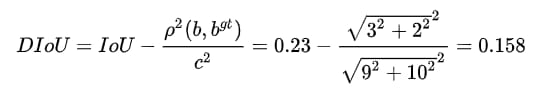
4.3 DIoUの実装
import numpy as np
import IoU
# box:[up, left, down, right]
box1 = [0,0,8,6]
box2 = [2,3,10,9]
def DIoU(box1, box2):
# Calculate the diagonal length
y1,x1,y2,x2 = box1
y3,x3,y4,x4 = box2
C = np.sqrt((max(x1,x2,x3,x4)-min(x1,x2,x3,x4))**2 + \
(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))**2)
# Calculate the center point distance
point_1 = ((x2+x1)/2, (y2+y1)/2)
point_2 = ((x4+x3)/2, (y4+y3)/2)
D = np.sqrt((point_2[0]-point_1[0])**2 + \
(point_2[1]-point_1[1])**2)
# Calculate IoU
iou = IoU(box1, box2)
# Calculate the percentage of blank parts
lens = D**2 / C**2
diou = iou - lens
return diou
DIoU(box1, box2)
アウト:0.1589460263493413
5 CIoU
5.1 CIoUの原則
CIoUの正式名称はComplete IoUで、DIoUをベースに2つの長方形の縦横比も同時に考慮する、つまり形状の類似性を考慮し、CIoUは次のように計算される。
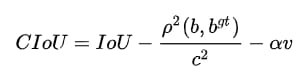
ここで、αは重み関数、vはアスペクト比の類似度を測るために使用される。
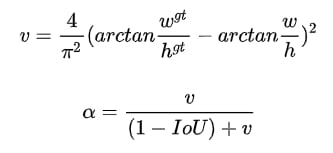
このように、CIoUはDIoUに画像の類似性の影響因子を加えたものなので、2フレーム間の差異をよりよく反映することができます。
もう一つ注意しなければならないのは、CIoUをLossとして使う場合、バックプロパゲーションの計算にはvの勾配も関わってくるということです。
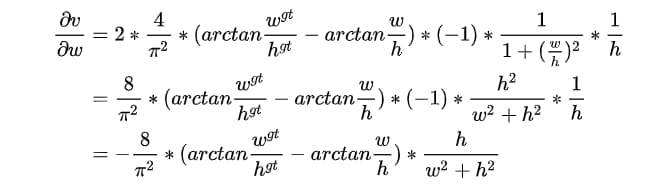
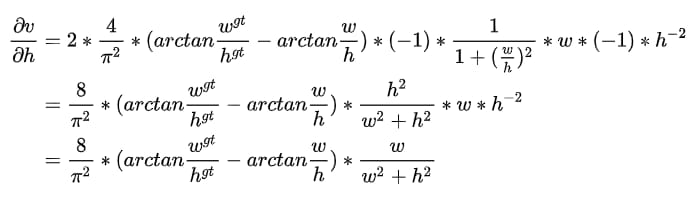
矩形のwとhがともに1より小さいと、w2+h2の値が小さくなり、勾配が爆発しやすくなるので、vの勾配を計算するときは、素直に
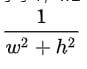 を1として計算します。
を1として計算します。
この時点でようやく、2つの画像の重なり率、グラフ距離、形状の類似性(矩形の縦横比)を組み合わせた指標を得るという当初の目的を達成することができたのです。
注:CIoU論文とDIoUは同じ論文です。
5.2 CIoUの計算
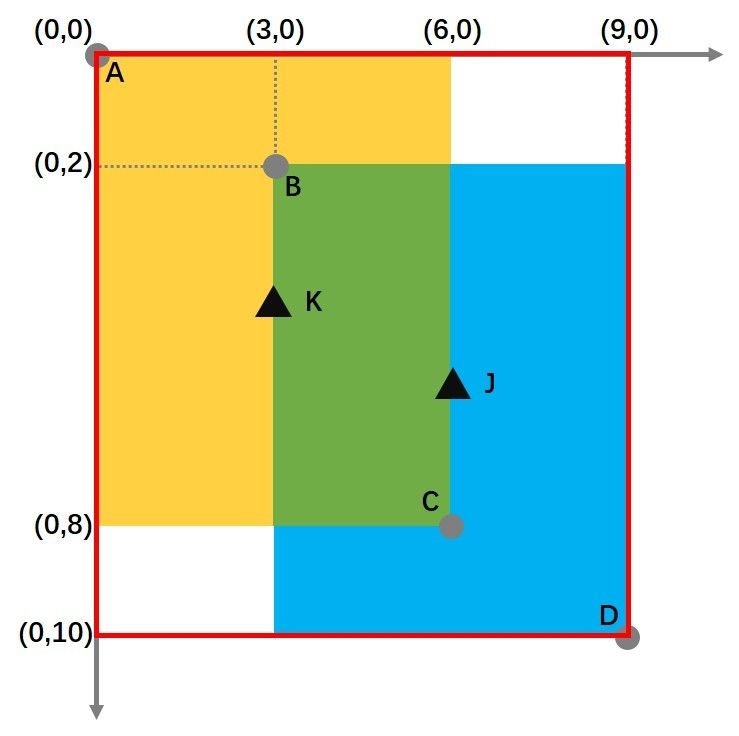
黄色い箱の中心点Kと青い箱の中心点Jの座標は、次のように計算できます。
K: (3,4) J: (6,6)
この時点でのCIoUの計算式は
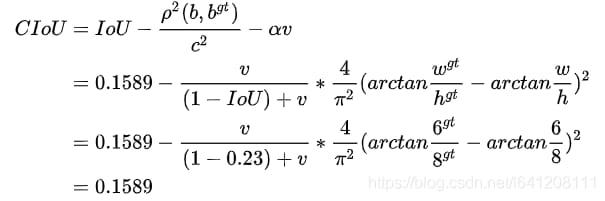
2つの長方形の形状は最初から同じであり、形状ペナルティは0なので、CIoU=DIoUとなり、2つの形状の差が大きいほど、CIoUはDIoUに比べて小さくなるのです。
5.3 CIoUの実装
import numpy as np
import math
import IoU
import DIoU
# box:[up, left, down, right]
box1 = [0,0,8,6]
box2 = [2,3,10,9]
def CIoU(box1, box2):
y1,x1,y2,x2 = box1
y3,x3,y4,x4 = box2
iou = IoU(box1, box2)
diou = DIoU(box1, box2)
v = 4 / math.pi**2 * (math.atan((x2-x1)/(y2-y1)) - \
math.atan((x4-x3)/(y4-y3)))**2 + 1e-5
alpha = v / ((1 - iou) + v)
ciou = diou - alpha * v
return ciou
CIoU(box1, box2)
アウト:0.1589460263493413
参考
https://zhuanlan.zhihu.com/p/111013447
https://www.zhihu.com/people/li-ge-35-18/posts
関連
-
などの警告を出しながらFaster-RCNNを実行します。RuntimeWarning: invalid value encountered in greater_equal などの警告が表示されます。
-
xx.exe の 0x00007FF7A7B64FB3 でスローされた例外: 0xC0000005: 場所 0x00 を読み取るアクセス違反
-
深層学習トラッキングアルゴリズム概要
-
トーチの取り付けと使用
-
参照用シークレットを呼び出す:BN層詳細解説
-
PackagesNotFoundError: 次のパッケージは、現在のチャンネルから利用できません ソリューション
-
Win10でanacondaのconda activateで環境起動時にエラーが出る場合はどうすればいいのでしょうか?
-
tensorflow experience code error Adding visible gpu devices: 0 , モジュール 'tensorflow' には 'Session' という属性がありません。
-
Tensorflow-gpu2.0.0インストールとtensorflow-gpuインストール成功のテストプログラム。
-
AttributeError: 'tuple' オブジェクトには 'log_softmax' という属性がありません。
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
py-faster-rcnn/lib の make でエラー: コマンドラインオプション '-Wdate-time' が認識されない
-
[Tensorflow-Error】CUDA_ERROR_OUT_OF_MEMORY:メモリが不足しています。
-
tensorflowをインポートしています。ImportError: libcublas.so.9.0: cannot open shared object file: No such file or director
-
U-netのソースコード解説(Keras編)
-
カーネルが死んだようです」の解決法。自動的に再起動します" の解決方法
-
caffeのインストールで「error : too few arguments in function call」エラーが発生する。
-
TypeError: 'module' object is not callable solution to [Keras] call "merge".
-
pytorchはエラーを報告します。ValueError: num_samples は正の整数値であるべきですが、num_samples=0 となりました。
-
TensorFlow実行時エラー、AttributeError: モジュール 'pandas' には 'computation' という属性がない。
-
AttributeError: モジュール 'pandas' には 'core' という属性がありません。
