Batch Normalization（BN：バッチ正規化：学習中に中間層のデータ分布が変化する問題を解決し、勾配の消滅や爆発を防ぎ、学習を高速化する。）

1. なぜ入力データを正規化する必要があるのか（正規化データ）？

        正規化することで得られるメリットは何ですか？一方、学習データのバッチごとに分布が異なる場合（バッチ勾配降下法）、ネットワークは反復ごとに異なる分布に適応するように学習しなければならず、ネットワークの学習速度が大きく低下します。データの正規化前処理が必要なのはまさにこのためです。

        ディープネットワークの学習は、ネットワークの最初の数層における小さな変化が、後の層で累積的に増幅されるという複雑なプロセスです。ネットワークのある層で入力データの分布が変わると、その層はその新しいデータ分布を学習するために適応する必要があるので、学習中に学習データの分布が変化し続けると、ネットワークの学習速度に影響を与えることになるのです。

2. BN学習  

1) 確率的勾配降下法（SGD）はディープネットワークの学習にシンプルで効率的であるが、学習率、パラメータ初期化、重み減衰係数、ドロップアウト率などのパラメータを人為的に選択しなければならない欠点がある。これらのパラメータの選択は学習結果に大きく影響するため、パラメータのチューニングに多くの時間を浪費しています。そこでBNでは、より意図的に、よりゆっくりとパラメータをチューニングすることができる。

2) ニューラルネットワークを一度学習させると、その後はパラメータの更新が発生し、入力層のデータ（サンプルごとに人為的に正規化した入力層データなので）に加えて、学習中に、先の層の学習パラメータの更新が後の層の入力データ分布に変化をもたらすので、後のネットワークの各層の入力データ分布が常に変化していることになります。ネットワークの第2層を例にとると、第1層のパラメータと入力から計算される第2層の入力と、第1層のパラメータは学習過程でずっと変化しているので、必然的に後方の各層の入力データ分布に変化が生じます。このような学習過程におけるネットワークの中間層のデータ分布の変化を、我々は "Internal Covariate Shift" と呼んでいます。本稿で提案するアルゴリズムは、学習中に中間層のデータ分布が変化する状況を解決するものであり、そのアルゴリズムであるBatch Normalizationが誕生したわけです。

3）BNの位置づけ：活性化関数層、畳み込み層、完全連結層、プーリング層と同様に、BN（Batch Normalization）もネットワークの層の一つである。

4) BN の本質的な原理：ネットワークの各入力層において、別の正規化層を挿入する、つまり、最初に正規化処理を行い（正規化：平均 0、分散 1）、次の層のネットワークに移行する。しかし、文献正規化層は我々が考えるほど単純ではなく、学習可能でパラメータ化された（γ, β）ネットワーク層である。

3. BNの役割

 1) ネットワークを流れる流れの勾配を改善する

 2）より大きな学習率を可能にし、学習速度を大幅に向上させる。

      初期の学習率を比較的大きく選択できるため、学習速度を飛躍的に向上させることができます。以前は、ネットワークの学習の途中でも、ゆっくりと学習率を調整し、さらに学習率を下げるには何が良いかを考えなければなりませんでしたが、今は非常に大きな初期学習率を使うことができ、このアルゴリズムは非常に早く収束するので、学習率は大きな速度で減衰していきます。もちろんこのアルゴリズムは、学習率を小さく選んでも、学習収束が速いという性質があるので、以前より早く収束します

 3）初期化に対する強い依存度を下げる

 4) 正則化戦略の改善：正則化の一形態として、ドロップアウトの必要性を若干低減

       オーバーフィッティングにおいて、ドロップアウトとL2正則化のパラメータの選択に悩まされることはもうありません。BNでは、ネットワークの汎化性を向上させる性質があるため、この2つのパラメータを削除したり、より小さなL2正則化制約を選択したりすることができるのです。

 5) BN自体が正規化されたネットワーク層であるため、局所応答正規化層（局所応答正規化はAlexnetネットワークで使われている手法で、視覚に詳しい方ならご存知でしょう）を使う必要がなくなりました。

6) 学習データを完全に分割することができる（学習の各バッチで特定のサンプルが頻繁に選ばれるのを防ぐため、文献ではこれで1％精度が向上するとしている）。

注）上記は学習過程である。テストでは、小ロットによる平均値や分散（mean/std）は計算されず、学習過程での活性化値の平均値とすることができる。

参考：https://www.cnblogs.com/king-lps/p/8378561.html
---------- ------
著作権について これはCSDNブロガー"Wang Xiaobo"によるオリジナル記事です。CC 4.0 BY-SA著作権契約に従い、原典のリンクとこの声明を記載してください。
元記事へのリンク： https://blog.csdn.net/qq_38900441/article/details/106047525

バッチ正規化（後にBNと表記）を理解してから、初心者がBNを正しく使えるようになるまでの道のりは長いです。以下、メモです。

BNについてネットで最も検索されているのは、原理の導出と関連論文です。

例えば

http://blog.csdn.net/Fate_fjh/article/details/53375881

https://www.jianshu.com/p/0312e04e4e83

しかし、これでは実際に使うときに困りますし、早く使いたいパートナーにもあまり親切とは言えません。私たちエンジニアは、まず使ってみてから原理原則を理解することが大切だと考えています へぇー!

BN層の実装やコード例に関する記事はいくつかありますが、スムーズに動くものはごくわずかです。なぜなら、BNを使うことは、畳み込み層のような層実装を書くのとは違うからです。BN層は2つの学習可能なパラメータと2つの学習不可能なパラメータを含むので、学習コードをどのように保存し、推論コードをどのようにロードするかという重要な問題を含んでいます。このステップについては、関連するブログがあり、非常に参考になります。

例

https://www.cnblogs.com/hrlnw/p/7227447.html

他の人が言っていることがわかりやすいので、真似するのは簡単だったのでは？つけられるコードでは、BN機能が正しくできないでしょう。私が間違ってコピーしたのか、誰かが重要な部分を見落としたのかわかりませんが。とにかく、あなたのmoving_mean/moving_varianceは正しいとは思えません。基本的に、中国のページではこの問題の解決策を見つけるのは難しいです。

さて、検索すべきキーワードは、BN/パラメータ保存/平均値スライドなどでしょうか。幸いなことに、tensorflowのgithubにはヒントがあります。

https://github.com/tensorflow/tensorflow/issues/14809

https://github.com/tensorflow/tensorflow/issues/15250

このように、BN機能を正しく使えない人は本当に多いのですが、最も便利な問題の1つは

https://github.com/tensorflow/tensorflow/issues/1122#issuecomment-280325584

ここでは、私が長年抱えていた問題を解決するために、完全に動作するBN関数コードをこしらえ、私を興奮させました。

ウェブからの知識、ウェブへの献身。この成果は一人では共有できないので、あえてここで改めて共有します。

----------------------------------------------------------------- gorgeous divider ----------------------------------------------------------- -----------------

BN機能全体は、1.BN層の実装、2.学習時の更新と終了後の保存、3.予測時の読み込みの3つの部分からなる必要があります。

1. BN層の実装。

以前からいる人なら、ここでBNを実装する方法を3つくらいは知っているはずですが、私はそのうちの1つしか成功していないので、他の人が補足してくれることを期待します。

def bn_layer(x, scope, is_training, epsilon=0.001, decay=0.99, reuse=None):

    """

    Performs a batch normalization layer

    Args:

        x: input tensor

        scope: scope name

        is_training: python boolean value

        epsilon: the variance epsilon - a small float number to avoid dividing by 0

        decay: the moving average decay

    Returns:

        The ops of a batch normalization layer

    """

    with tf.variable_scope(scope, reuse=reuse):

        shape = x.get_shape().as_list()

        # gamma: a trainable scale factor

        gamma = tf.get_variable(scope+"_gamma", shape[-1], initializer=tf.constant_initializer(1.0), trainable=True)

        # beta: a trainable shift value

        beta = tf.get_variable(scope+"_beta", shape[-1], initializer=tf.constant_initializer(0.0), trainable=True)

        moving_avg = tf.get_variable(scope+"_moving_mean", shape[-1], initializer=tf.constant_initializer(0.0), trainable=False)

        moving_var = tf.get_variable(scope+"_moving_variance", shape[-1], initializer=tf.constant_initializer(1.0), trainable=False)

        if is_training:

            # tf.nn.moments == Calculate the mean and the variance of the tensor x

            avg, var = tf.nn.moments(x, np.range(len(shape)-1), keep_dims=True)

            avg=tf.reshape(avg, [avg.shape.as_list()[-1]])

            var=tf.reshape(var, [var.shape.as_list()[-1]])

            #update_moving_avg = moving_averages.assign_moving_average(moving_avg, avg, decay)

            update_moving_avg = tf.assign(moving_avg, moving_avg*decay+avg*(1-decay))

            #update_moving_var = moving_averages.assign_moving_average(moving_var, var, decay)

            update_moving_var = tf.assign(moving_var, moving_var*decay+var*(1-decay))

            control_inputs = [update_moving_avg, update_moving_var]

        else:

            avg = moving_avg

            var = moving_var

            control_inputs = []

        with tf.control_dependencies(control_inputs):

            output = tf.nn.batch_normalization(x, avg, var, offset=beta, scale=gamma, variance_epsilon=epsilon)

    return output

def bn_layer_top(x, scope, is_training, epsilon=0.001, decay=0.99):

    """

    Returns a batch normalization layer that automatically switches between train and test phases based on the

    tensor is_training

    Args:

        x: input tensor

        scope: scope name

        is_training: boolean tensor or variable

        epsilon: epsilon parameter - see batch_norm_layer

        decay: epsilon parameter - see batch_norm_layer

    Returns:

        The correct batch normalization layer based on the value of is_training

    """

    #assert isinstance(is_training, (ops.Tensor, variables.Variable)) and is_training.dtype == tf.bool

    return tf.cond(

        is_training,

        lambda: bn_layer(x=x, scope=scope, epsilon=epsilon, decay=decay, is_training=True, reuse=None),

        lambda: bn_layer(x=x, scope=scope, epsilon=epsilon, decay=decay, is_training=False, reuse=True),

    )

Here the parameters epsilon=0.001, decay=0.99 can be adjusted by yourself.



2. Update during training and save after completion.

Add the following code to the training code:

update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)

with tf.control_dependencies(update_ops):

    train = tf.train.AdamOptimizer(learning_rate=lr).minimize(cost)

This is used to update the parameters.

var_list = tf.trainable_variables()

g_list = tf.global_variables()

bn_moving_vars = [gfor gin g_listif 'moving_mean' in g.name]

bn_moving_vars += [gfor gin g_listif 'moving_variance' in g.name]

var_list += bn_moving_vars

train_saver = tf.train.Saver(var_list=var_list)

This is used to save the bn untrainable parameters.

3. Load at prediction.

# get moving avg

var_list = tf.tr

正則化制約 l1, l2 を tensorflow フレームワークに追加する。

https://blog.csdn.net/Airuio/article/details/84025973

I. 基本的な正則化関数

tf.contrib.layers.l1_regularizer(scale, scope=None)

を実行するために使用されるコードを返します。 L1 というシグネチャを持つ正規化関数です。 func(weights) . 
パラメータ :

• scale: 正規の項の係数。
• scope: オプション

  scope name
  

tf.contrib.layers.l2_regularizer(scale, scope=None)

まず、tf.contrib.lays.l2_regularizer(weight_decay)が何を行うかを見てみましょう。

<テーブル

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

import
tensorflow as tf
sess
=
tf.Session()
weight_decay
=
0.1
tmp
=
tf.constant([
0
,
1
,
2
,
3
],dtype
=
tf.float32)
"""
l2_reg=tf.contrib.layers.l2_regularizer(weight_decay)
a=tf.get_variable("I_am_a",regularizer=l2_reg,initializer=tmp)
"""
#** Equivalent code for the above code
a
=
tf.get_variable(
"I_am_a"
,initializer
=
tmp)
a2
=
tf.reduce_sum(a
*
a)
*
weight_decay
/
2
;
a3
=
tf.get_variable(a.name.split(
":"
)[
0
]
+
"/Regularizer/l2_regularizer"
,initializer
=
a2)
tf.add_to_collection(tf.GraphKeys.REGULARIZATION_LOSSES,a2)
#**
sess.run(tf.global_variables_initializer())
keys 
=
tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
for
key 
in
keys:
print
(
"%s : %s"
%
(key.name,sess.run(key)))

tf.contrib.layers.l2_regularizer が行うことを簡単にモックアップすることができますが、醜いコードになります。

以下は、L2正則化をより完璧に実装したものである。

<テーブル

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

import
tensorflow as tf
sess
=
tf.Session()
weight_decay
=
0.1
#(1) Define weight_decay
l2_reg
=
tf.contrib.layers.l2_regularizer(weight_decay)           
#(2) Define l2_regularizer()
tmp
=
tf.constant([
0
,
1
,
2
,
3
],dtype
=
tf.float32)
a
=
tf.get_variable(
"I_am_a"
,regularizer
=
l2_reg,initializer
=
tmp)  
#(3) Create variable, l2_regularizer copy to regularizer parameter.
#Sighting the REXXX_LOSSES collection
#regularizer definition will add a to the REGULARIZATION_LOSSES set
print
(
"Global Set:"
)
keys 
=
tf.get_collection(
"variables"
)
for
key 

in
keys:
print
(key.name)
print
(
"Regular Set:"
)
keys 
=
tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
for
key 
in
keys:
print
(key.name)
print
(
"--------------------"
)
sess.run(tf.global_variables_initializer())
print
(sess.run(a))
reg_set
=
tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)   
#(4) then the REGULARIAZTION_LOSSES collection will contain the sum of all the parameters that have been weight_decayed, summing them
l2_loss
=
tf.add_n(reg_set)
print
(
"loss=%s"
%
(sess.run(l2_loss)))
"""
The output here is 0.7, i.e.:
weight_decay*sigmal(w*2)/2=0.1*(0*0+1*1+2*2+3*3)/2=0.7
It's actually easy to write the code yourself, and it looks more formal with the API.
In the network model, just add l2_loss to the loss directly. (The loss becomes larger and the execution train naturally decays)
"""

トップページに戻る

II. 正則化手法の追加

a. 独自のアプローチ

正則化はコレクションに対してよく使われるが、以下は最も原始的な正則化の追加方法である（変数宣言の後に直接'loss'コレクションやtf.GraphKeys.LOESSESに追加しても効果がある）。

<テーブル

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

import
tensorflow as tf
import
numpy as np
def
get_weights(shape, lambd):
var 
=
tf.Variable(tf.random_normal(shape), dtype
=
tf.float32)
tf.add_to_collection(
'losses'
, tf.contrib.layers.l2_regularizer(lambd)(var))
return
var
x 
=
tf.placeholder(tf.float32, shape
=
(
None
, 
2
))
y_ 
=
tf.placeholder(tf.float32, shape
=
(
None
, 
1
))
batch_size 
=
8
layer_dimension 
=
[
2
, 
10
, 
10
, 
10
, 
1
]
n_layers 
=
len
(layer_dimension)
cur_lay 
=
x
in_dimension 
=
layer_dimension[
0
]
for
i 
in
range
(
1
, n_layers):
out_dimension 
=
layer_dimension[i]
weights 
=
get_weights([in_dimension, out_dimension], 
0.001
)
bias 
=
tf.Variable(tf.constant(
0.1
, shape
=
[out_dimension]))
cur_lay 
=
tf.nn.relu(tf.matmul(cur_lay, weights)
+
bias)
in_dimension 
=
layer_dimension[i]
mess_loss 
=
tf.reduce_mean(tf.square(y_
-

cur_lay))
tf.add_to_collection(
'losses'
, mess_loss)
loss 
=
tf.add_n(tf.get_collection(
'losses'
))

b, tf.contrib.layers.apply_regularization(regularizer, weights_list=None)

まず、パラメータを見てみましょう。

• regularizer: 前のステップで作成した正則化メソッドです。
• weights_list: レギュラライザーメソッドのパラメータリスト。 None を取ります。 GraphKeys.WEIGHTS で weights .

関数はスカラーを返します Tensor 一方、スカラー Tensor にも保存されます。 GraphKeys.REGULARIZATION_LOSSES の中で、この Tensor は、通常の期間損失を計算する方法を保持しています。

tensorflow で Tensor は、実行時に計算する値を保持するパス（メソッド）です。 tensorflow バックエンドが計算するのは Tensor の値に対応する。

あとは、この正規項損失を損失関数に追加するだけです。

を例として挙げます。

重み = tf.constant([[1.0, -2.0], [-3.0, 4.0]])
weight1 = tf.constant([[1.0, -2.0], [-3.0, 4.0]])
l2_reg = tf.contrib.layers.l2_regularizer(0.5)
tf.Session() を sess とした場合。
    # 出力は (|1|+|-2|+|-3|+|4|)*0.5=5 です。
    print(sess.run(tf.contrib.layers.apply_regularization(regularizer=l2_reg,weights_list=[weight,weight1])))
    # 出力は (1²+(-2)²+(-3)²+4²)/2*0.5=7.5 です。
    # TensorFlowは導出をより簡潔にするため、L2の正則化された損失値を2で割り算する
    print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(weight)))

自分で手動で定義する場合 weight の場合、手動で weight から GraphKeys.WEIGHTS が、もし layer を使えば、誰かがすでに処理してくれているので、悩む必要はありません。( It's best to verify the tf.GraphKeys.WEIGHTS をすべて表示するかどうかを確認します。 weights , ピットされるのを防ぐため)

c. スリムを使う

slim を使うのはもっと簡単です。

<テーブル

1

2

3

4

with slim.arg_scope([slim.conv2d, slim.fully_connected],
activation_fn
=
tf.nn.relu,
weights_regularizer
=
slim.l2_regularizer(weight_decay)).
pass

Pythonによる勾配降下の実装と解析・可視化例

コードとサンプルは、ブロガーのgithubからダウンロードできます。

https://github.com/Airuio/Implementing-the-method-of-gradient-descent-by-using-Python-

前回は、最も原始的なパーセプトロンアルゴリズムについて説明しましたが、このアルゴリズムは収束のみを目的としており、サンプルに基づく最適解が得られないことがよくあります。勾配降下法は損失関数を最小化することを目的としており、一般に原始的なパーセプトロンアルゴリズムよりも精度の高い解を得ることができます。

勾配降下アルゴリズムの原理を下図に示す。

以上の原理で重み係数とMin値を更新することにより、最終的な解が得られます。

この原理の実装は、以下のコードで行うことができる。# 勾配降下法の実装。

import numpy as np
class AdalineGD(object):
    def __init__(self,eta=0.01,n_iter=50): #define hyperparameter learning rate and number of iterations
        self.eta = eta
        self.n_iter = n_iter
    
    def fit(self,X,y): #define the weight coefficient w and the loss function cost
        self.w_ = np.zeros(1+X.shape[1])
        self.cost_ = []
        
        for i in range(self.n_iter): # update the weights
            output = self.net_input(X) # calculate the predicted value
            errors = (y - output) # count errors
            self.w_[1:] += self.eta*X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum()/2.0 # loss function
            self.cost_.append(cost)
        return self

    def net_input(self,X):
        return np.dot(X,self.w_[1:]) + self.w_[0]
    
    def activation(self,X):
        return self.net_input(X) 

    def predict(self, X):

        return np.where(self.activation(X) >= 0.0, 1, -1)

上記のアルゴリズムは、重みパラメータを更新するために、勾配降下法を実装している。このモジュールをAdaline_achieveと名付け、Iris lirsデータセットに基づき、以下のようにアルゴリズムの検証を行う。

from Adaline_achieve import AdalineGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

df = pd.read_excel(io = 'lris.xlsx',header = None) # read data as Dataframe structure, no header rows
y = df.iloc[0:100,4].values #fetch the first 100 columns of data, 4 columns of identification
y = np.where(y == 'Iris-setosa', -1,1)
X = df.iloc[0:100,[0,2]].values #iloc for the selected table area, here to take two-dimensional features for classification, values for the return of the table without the index

plt.scatter(X[:50,0],X[0:50,1],color = 'red',marker = 'o', label = 'setosa')
plt.scatter(X[50:100,0],X[50:100,1],color = 'blue',marker = 'x', label = 'versicolor')
plt.xlabel('petal lenth')
plt.ylabel('sepal lenth')
plt.legend(loc = 2) # draw the label and the label's location parameters      
plt.show() # show the graph
#The above six lines have nothing to do with classification, but simply to visualize the distribution of the two pieces of data

fig,ax = plt.subplots(nrows = 1 , ncols = 2, figsize = (8,4))    
'''
Complete the task of classifying at different learning rates and present the results
plt.subplots(nrows = 1 , ncols = 2, figsize = (8,4) where nrows means several rows of figures and ncols means several columns
figsize is the image size.
'''
ada1 = AdalineGD(eta = 0.01,n_iter = 10).fit(X,y)
ax[0].plot(range(1,len(ada1.cost_) + 1), np.log10(ada1.cost_) , marker = 'o')
ax[0].set_xlabel('Epoches')
ax[0].set_ylabel('log(ada1.cost_)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(eta = 0.0001,n_iter = 10).fit(X,y)
ax[1].plot(range(1,len(ada2.cost_) + 1), ada2.cost_ , marker = 'o')
ax[1].set_xlabel('Epoches')
ax[1].set_ylabel('ada1.cost_')
ax[1].set_title('Adaline - Learning rate 0.01')
plt.show()
'''
From the above obtained result plots, we can see that too large a learning rate will lead to non-convergence and too small will lead to slow convergence
Using the method of data normalization and normalization can make the gradient descent method achieve better results
Taking the mean and standard deviation of the sample features at the same dimension, the normalized value is equal to
(original value - mean)/standard deviation, which can be easily obtained by using the mean and std methods in numpy
'''
X_std = np.copy(X) # normalize and normalize the sample features
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()


ada = AdalineGD(eta = 0.01, n_iter = 15)
ada.fit(X_std,y)
def plot_decision_region(X,y,classifier,resolution = 0.02):
    markers = ('s','x','o','~','v')
    colors = ('red','blue',

その結果は、次の図のようになります。

---------- ---
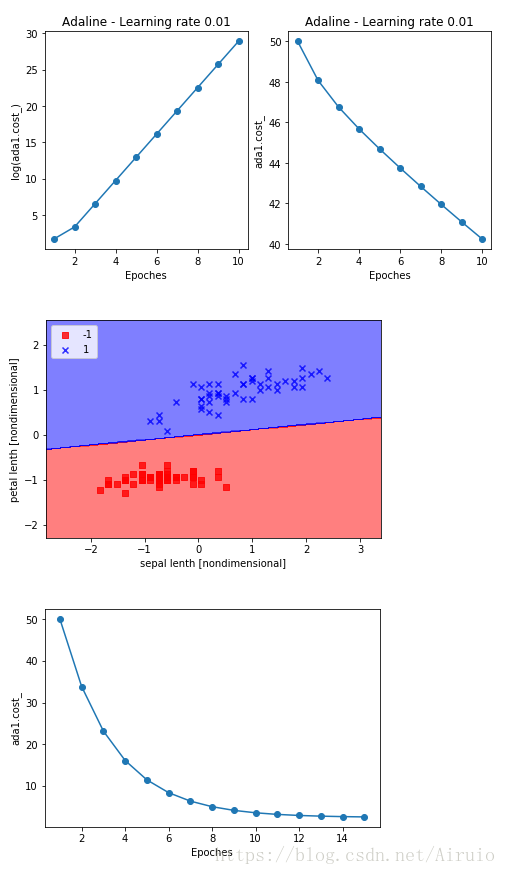
著作権について この記事はCSDNブロガー "Airuio" によるオリジナル記事です。CC 4.0 BY-SA 著作権契約に則り、元ソースへのリンクとこのステートメントを記載してください。
元記事へのリンク： https://blog.csdn.net/Airuio/article/details/80956661