取得元：http://blog.csdn.net/google19890102/article/details/50522945

I. 分類アルゴリズムにおける損失関数

分類アルゴリズムにおいて、損失関数は通常、損失項と正則項の和で表すことができる、すなわち、次のような形式をとる。

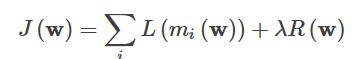
ここで、Lは損失項、Rは正規の項である。 miは具体的には次のような形式である。

<イグ

ロスタームについては、主な形態は以下の通りです。

• 0-1敗
• ログアウト
• ヒンジ損失
• 指数関数的損失
• 知覚的損失

1. 0-1損失関数

分類問題では、関数の正負の符号をパターン判断に利用することができる。関数値の大きさ自体はあまり重要ではなく、0-1損失関数は予測値fwが真値yと同じ符号を持つかどうかを比較する。0-1損失の具体的な形は以下の通りである。

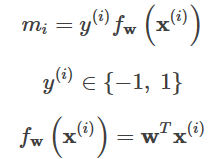
上記の関数は、以下の関数と等価である。

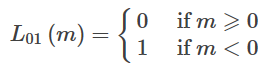
0-1損失はm値の大きさには依存せず、mの正負の符号にのみ依存する。0-1損失は非凸関数であり、解法上の欠点が多く、実務では0-1損失関数の代理を損失関数として選択する基準として使われるのが一般的である。

<スパン 上記の定義が厳しすぎることがおわかりいただけると思います。真の値が1で、予測値が0.999であれば、予測は正しいはずですが、上記の定義は明らかに間違っていると判断されます .

2. 対数損失関数

2.1, 対数損失

Log lossは0-1損失関数の代理関数であり、Log lossの具体的な形は以下の通りである。

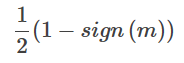
Log lossを用いる代表的な分類器として、Logistic Regressionアルゴリズムがあります。

2.2. ロジスティック回帰アルゴリズムの損失関数

ロジスティック回帰アルゴリズムでは、分類器は次のように表現されます。

ここで、y∈{0, 1}である。パラメータwの一つを解くには、通常、次のような大尤度推定の方法が用いられる。

1. 尤度関数

どこ

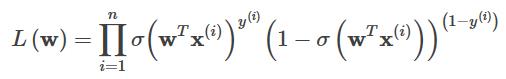
2. 対数尤度

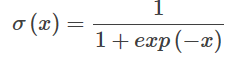
3. 解くべきは対数尤度が最大値を得るwであり、その最小値を求めることに変換できる。

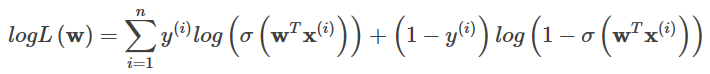
これがクロスエントロピーの具体的な形です。

2.3. 両者の等価性

Log lossの具体的な形態は、なので。

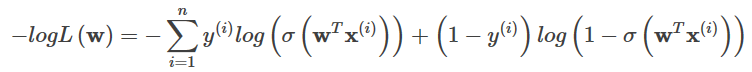
ここで、m = y*fw,y ∈ {-1, 1}, そしてLog損失関数は次のような形式をとる。

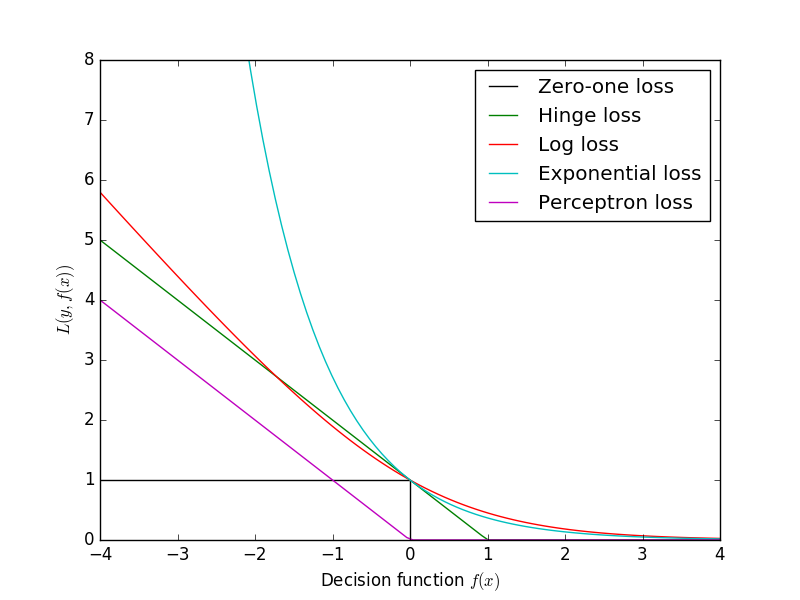
ロジスティック回帰はLog lossと同じ形なので、等価である。Log lossと0-1 lossの関係は、下図のようになる。

3. ヒンジ損失関数

3.1, ヒンジ損失

ヒンジロスは0-1損失関数の代理関数であり、その具体的な形は次の通りである。

max(0, 1-m)

ヒンジロスを用いた代表的な分類器として、SVMアルゴリズムがあります。

3.2. SVMの損失関数

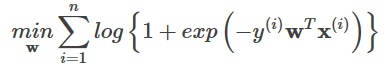
3.3. の等価性

ヒンジロスの場合。

max(0, 1 - m)

最適化の目的は、以下のことを要求することである。

上記の関数fwに切片γを導入する、すなわち

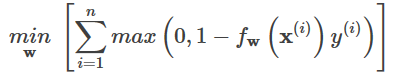
で、上の最適化問題にL2正規を追加すると、次のようになります。

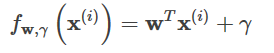
ここまでで、次の不等式が成り立つとする。

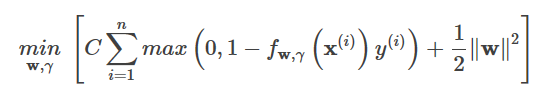
コンストレイントは

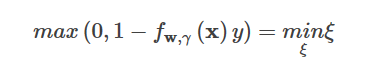
すると、ヒンジの最小化問題は次のようになる。

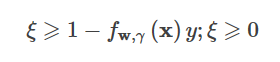
コンストレイントは

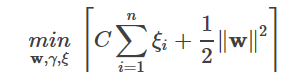
これはソフトスペースSVMと一致し、ソフトスペースSVMがHinge lossにL2ノルムを加えたものであることを示しています。

4. 指数関数的損失

4.1, 指数的損失

指数損失は0-1損失関数の代理関数であり、指数損失の具体的な形は以下の通りである。

exp(-m)

指数関数的損失を用いる代表的な分類器として、AdaBoostアルゴリズムがあります。

4.2、AdaBoostの基礎知識

AdaBoostのアルゴリズムは、各サンプルと同様に各弱分類器に重みを割り当てるもので、弱分類器φに対して重みは

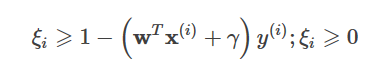
ここで、R(φ)は誤判定率を表す。各サンプルについて、重みは次のとおりである。

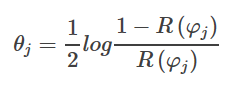
最終的な出力は、すべての分類器に重み付けをすることで得られます。

4.3. の等価性

指数関数的損失関数の場合。

exp(-m)

最適化される損失関数は、次のように求めることができる。

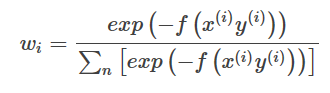
f～が学習済みの関数を表すと仮定すると、ある。

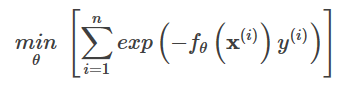
∑ i =1 n w i { <未定義 e x p ( θ )-

φを最小化することで、次のようになる。

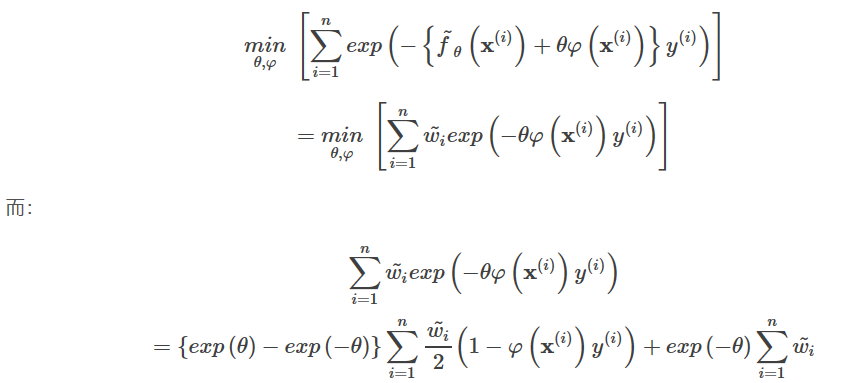
これを上の式に代入し、theatの最適解を求めると、次のようになる。

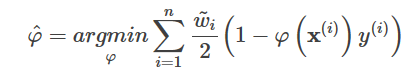
AdaBoostと同等であることがわかる。

5. 知覚的損失

5.1. 知覚的損失

知覚的損失はヒンジ損失の変形であり、知覚的損失の具体的な形態は以下の通りである。

max(0, -m)

知覚的損失を利用した代表的な分類器として、パーセプトロンアルゴリズムがある。

5.2. パーセプトロンアルゴリズムの損失関数

各サンプルが正しく分類されているかどうかを判断し、間違って分類されたサンプルだけを記録すればよいパーセプトロンアルゴリズムの損失関数は、次のようになります。

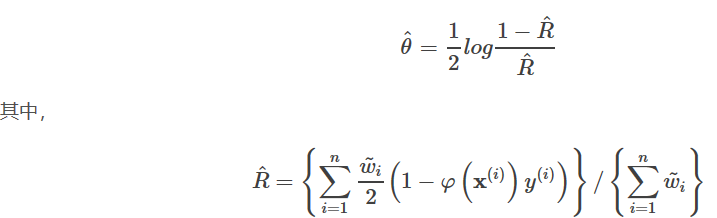
5.3. の等価性

知覚的損失の場合。

max(0, -m)

最適化のゴールは

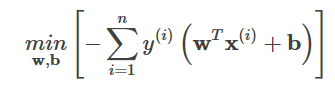
上の関数fwに切片bを導入する、すなわち

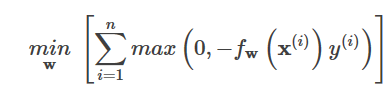
という形に変換されます。

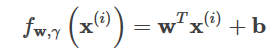
max関数の内容については、以下のことが知られている。

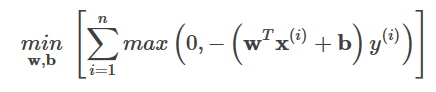
間違ったサンプルの場合は、あります。

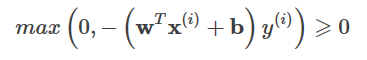
ヒンジ損失と同様に、以下の式が成り立つようにします。

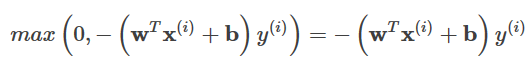
コンストレイントは

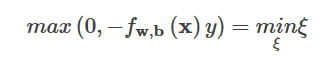
すると、知覚的損失はこうなる。

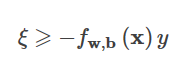
ということです。

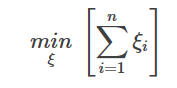
一方、知覚的損失は、サンプルのクラスが正しく決定されていればよく、決定境界からの距離は必要ない。この変更により、ヒンジ損失よりも単純になったが、一般化できるわけではない。

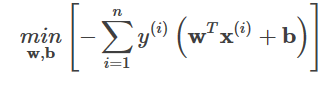
import matplotlib.pyplot as plt
import numpy as np

xmin, xmax = -4, 4
xx = np.linspace(xmin, xmax, 100)
plt.plot([xmin, 0, 0, xmax], [1, 1, 0, 0], 'k-', label="Zero-one loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0), 'g-', label="Hinge loss")
plt.plot(xx, np.log2(1 + np.exp(-xx)), 'r-', label="Log loss")
plt.plot(xx, np.exp(-xx), 'c-', label="Exponential loss")
plt.plot(xx, -np.minimum(xx, 0), 'm-', label="Perceptron loss")

plt.ylim((0, 8))
plt.legend(loc="upper right")
plt.xlabel(r"Decision function $f(x)$")
plt.ylabel("$L(y, f(x))$")
plt.show()

参考記事

• 機械学習応用のためのアドバイス

取得元：http://blog.csdn.net/u014313009/article/details/51043064

クロスエントロピコスト関数（CECF）は、人工ニューラルネットワーク（ANN）の予測値と実測値を測定する方法である。2次コスト関数よりも効果的にANNの学習を促進することができる。本稿では、クロスエントロピコスト関数を紹介する前に、2次コスト関数とその欠点について簡単に紹介する。

1. 二次コスト関数の欠点

        ANN設計の目的の1つは、人間と同じように機械が知識を学習できるようにすることである。人間が新しいことを分析することを学ぶとき、間違いに気づいたときの修正が大きければ大きいほど、その効果は大きい。例えば、バスケットボールのシュート。選手が自分のシュートが正しい方向から遠ざかっていることに気づいたとき、シュートの角度を大きく調整すればするほど、バスケットボールがバスケットに入るのが容易になる。同じように 私たちは次のように考えています：ANNを学習させたときの予測値と実測値の誤差が大きければ大きいほど 後方伝搬学習 予測値と実測値の誤差が大きいほど、学習時の各種パラメーターを大きく調整することで、学習の収束を早めることができる。 しかし、2次コスト関数を用いてANNを学習させた場合、誤差が大きいとパラメータチューニングの大きさが小さくなり、学習速度が遅くなる可能性があるという実用上の効果が見られる。

        例として、1つのニューロン（ANNの一般的な活性化関数としてシグモイド関数があり、本実験でもこれを使用）の2クラス分類の学習について、同一のサンプルデータx=1.0を入力（実際の分類y=0に相当）、それぞれの最初の順伝播後に異なる出力値が得られるようにパラメータをランダムに初期化、結果として異なる代理（誤差）を得た2つの実験を行っている。

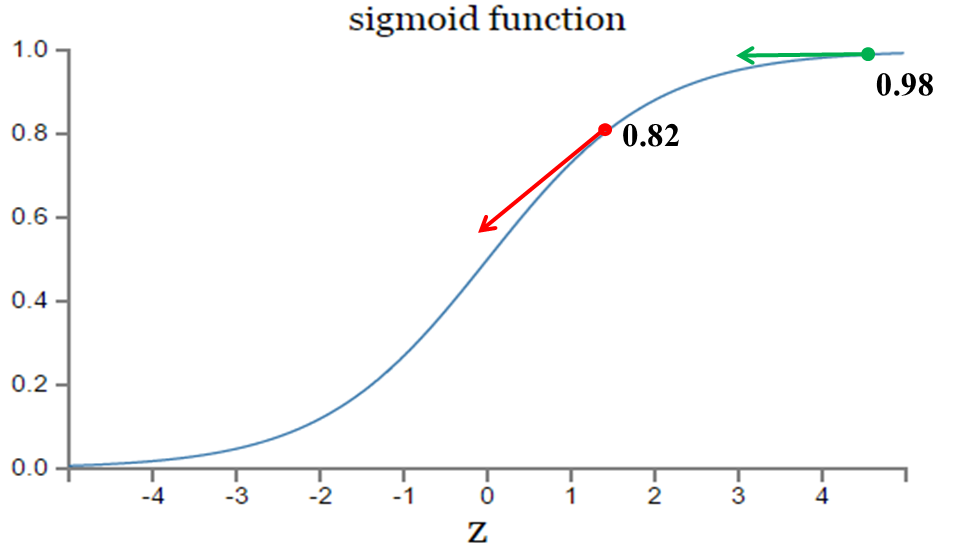
実験1：最初の出力値0.82

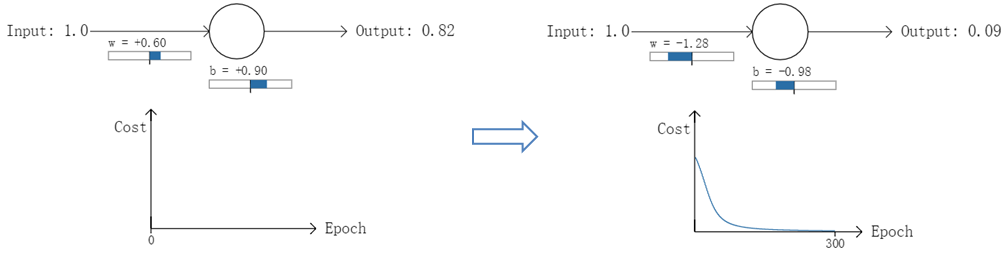
実験2：2回目の出力値0.98

        実験1では、最初の出力値が0.82（このサンプルの実際の値0に相当）になるようにパラメータをランダムに初期化し、300回の反復学習後に出力値が0.82から0.09に下がり、実際の値とほぼ同じになりました。一方、実験2では、最初の出力値は0.98であり、やはり300回の反復学習後に出力値は0.20までしか下がらない。

        2つの実験によるコストカーブを見ると 実験1のコストは学習の増加とともに急速に減少するが、実験2のコストは最初のうちは非常にゆっくりと減少する。直感的には、初期誤差が大きいほど収束は遅くなる .

        実は、誤差が大きいために学習が遅くなる原因は、2次コスト関数を用いていることにある。2次コスト関数の計算式は以下の通りである。

        ここで、C はコスト、x はサンプル、y は実測値、a は出力値、n はサンプルの総数である。簡単のため、2次コスト関数の場合、同じ1サンプルを例として説明する。

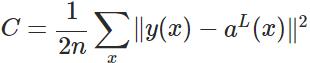
        現在、ANNのトレーニングに最も有効 アルゴリズム は バックプロパゲーションアルゴリズム . つまり、ANNの学習とは、コストを逆伝播してパラメータを調整し、コストを下げることを指向することである。パラメータは主にニューロン間の接続重みwと各ニューロン自身のバイアスbである．パラメータの調整は勾配降下アルゴリズムを用いて行われ，勾配方向に沿ってパラメータの大きさが調整される．

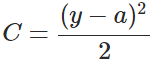
        ここで、z はニューロンへの入力を表します。 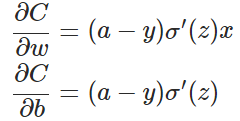は活性化関数を表す。上式から、wとbの勾配は活性化関数の勾配に比例し、活性化関数の勾配が大きいほど、wとbの大きさは早く調整され、学習は早く収束することがわかります。ニューラルネットワークでよく使われる活性化関数はシグモイド関数で、この関数の曲線は次のように示される。

        画像にあるように 実験2の初期出力値（0.98）は実験1の出力値（0.82）よりもかなり小さな勾配に相当するため、実験2のパラメータの勾配は実験1のそれよりもゆっくりと減少していくことになります。これが、初期コスト（誤差）が大きいほど学習速度が遅くなる理由である。 は、人間と違って、エラーが大きければ大きいほど、修正も大きくなり、その結果、学習も早くなるという我々の予想と一致しない。

        それなら、勾配が変化しない、あるいは大きく変化しない活性化関数を選べば解決するのでは、と言われるかもしれません。それは単純で残酷な解決策ですが、どんどん問題を大きくしてしまう可能性があります。また、シグモイドのような関数（tanh関数とか）は利点が多く、活性化関数に最適ですので、ぜひググってみてください。

2. クロスエントロピーのコスト関数

        考え方としては、活性化関数を切り替えるのではなく、2次コスト関数を切り替えて、クロスエントロピーのコスト関数を使うのです。

        ここで、x はサンプル、n はサンプルの総数を表す。そして、パラメータ w の勾配を再計算する。

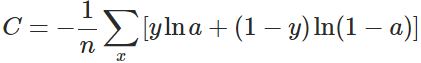
        このうち（具体的な証明は付録を参照）。

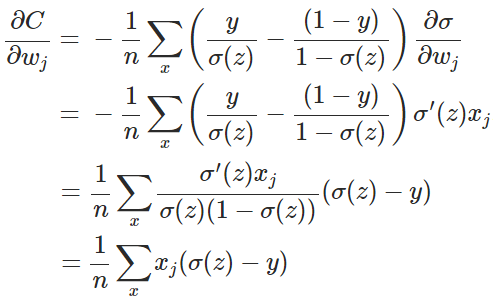
        従って、wの元の勾配式は の勾配式は削除され、さらに、この勾配式は は出力値と実測値との誤差を表している。したがって、誤差が大きいと勾配が大きくなり、パラメータwの調整が早くなり、学習速度が速くなる。同様に、bの勾配は次のように求められる。

        実際には、二次コスト関数よりもクロスエントロピーのコスト関数の方が良い学習結果をもたらすことが多いことが分かっている。すなわち、活性化関数としてシグモッド関数を用いる場合、クロスエントロピーのコスト関数を用いると、導出後の勾配変換は予測値と真値の残差に比例するようになる。したがって、学習速度が速く、安定している。

3. クロスエントロピーのコスト関数はどのように生成されるのですか？(これは定義ではなく、gradient backpropagationの観点からの一押しであることに注意してください）

        バイアスbの勾配計算を例にして、クロスエントロピーのコスト関数を導出せよ。

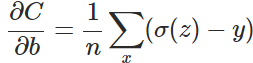
        サブセクション1において、2次コスト関数から導かれるbの勾配式は、次のようになる。

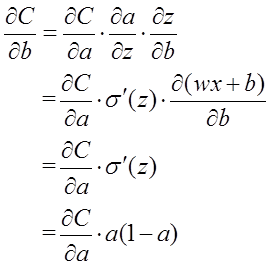
        を排除するために 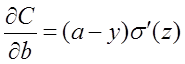となるようなコスト関数を求めたい。

        ウィットに富んでいる。

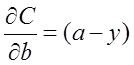
        両辺を積分すると

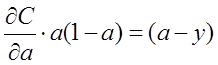
        そして、これが先ほど紹介したクロスエントロピーのコスト関数です。つまり、gradient backpropagationの観点から、バイアス計算については、もはや活性化関数がバイアス更新に影響を与えないようにさせるのです。このように、クロスエントロピーのコスト関数が導入されています。

<スパン パラメータと勾配の計算には活性化関数の勾配が含まれないことがわかり、活性化関数の勾配の減衰によるアルゴリズムの反復の遅さや収束性の悪さの問題を解決しています。

ソフトマックス機能

ロジスティック回帰の2値分類問題において sigmoid 関数を使って，入力 wx+b を (0,1) 区間に写像し，あるクラスに属する確率を求めます．この問題を多クラス分類の問題に一般化すると，関数 softmax 関数を用いて、出力値を確率値に正規化する。

ここでは、入力後に softmax 関数では、すでにモデルの出力Cがあり、Cは予測するカテゴリの数で、モデルは出力数Cの完全連結ネットワークの出力a、つまり出力はa1,a2,a3・・・・acとすることができる。

つまり、各サンプルについて、それがカテゴリーiに属する確率は

上記の式は、各カテゴリーに属する確率の和が1になることを保証している。

誘導体

について softmax 関数の導関数を求める。

<イグ

i番目の項の出力のj番目の項の入力に対する偏り。
代用品（Substitute softmax という関数式で表すと、次のようになります。

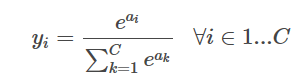
高校で習った導出の法則を使うと、for

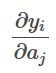
その誘導体は

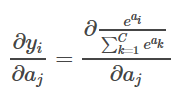
つまり、この例では

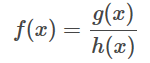
g

上の2つの式は、単なる直接の代入を表しているだけで、本当の意味での方程式ではありません。

exp(ai)、すなわちajに対するg(x) 微分の実施、別件で検討する。
1. i=jの場合、微分はexp(ai)となる。 
2. i≠j の場合、微分は0になる

もう一度、∑exp(ak)のajに関する微分を見ると、exp(aj)となる。

そこで、i＝jのとき。

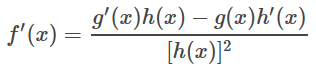
i ≠ j のとき。

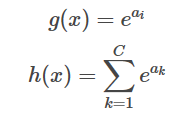
ここで、便宜上、∑ = ∑exp(ak) とする。

ソフトマックスの計算と数値的安定性

Pythonでは softmax という関数があります。

def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

で渡す [1, 2, 3, 4, 5] のベクトルです。

>>> softmax([1, 2, 3, 4, 5])
array([ 0.01165623, 0.03168492, 0.08612854, 0.23412166, 0.63640865])

ただし、入力値の方が大きい場合。

>>> softmax([1000, 2000, 3000, 4000, 5000])
array([ nan, nan, nan, nan, nan, nan])

を求める際に使用されるコードであるためです。 exp(x) を求めるとオーバーフローした。

import math
math.exp(1000)
# Traceback (most recent call last):
# File "
", line 1, in 

# OverflowError: math range error

この問題を回避するための簡単で効果的な方法は exp(x) の中に x の値があまり大きくもなく小さくもない。 softmax 関数の分数部分の上と下にそれぞれゼロでない定数を乗じたもの、すなわち

<イグ

ここでlog(E)は定数なので、Fと等しくすることができます。定数Fを加えても式は元の式と等しいので、定数Fをどう選ぶかを考えます。考え方としては、すべての入力を0付近にすることでexp(ai)の値があまり大きくならないので、Fの値を

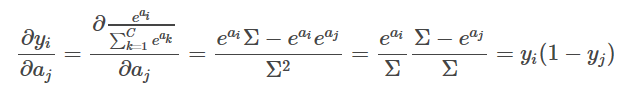
これは、すべての入力を0付近にシフトさせ（もちろん、すべての入力が数値的に近いと仮定して）、一方、最大値以外のすべての入力は、負のeベースの指数関数にシフトし、0に近いほど小さくなり、これは、以下を得るよりも良い。 nan を得るよりも良い結果となりました。

<ブロッククオート

def softmax(x):
    shift_x = x - np.max(x)
    exp_x = np.exp(shift_x)
    return exp_x / np.sum(exp_x)