[解決済み】円内のランダムな点を生成する（一律）。

質問

半径1.5mの円内に一様にランダムな点を生成したい。 R .

私は、区間 [0 ...] の中で一様にランダムな角度を選ぶだけで、その角度を実現できることに気づきました。2π）、半径は区間（0 .... R なぜなら、2つの半径が与えられた場合、小さい半径の点は大きい半径の点よりも互いに近くなるからです。

この件に関するブログエントリーを見つけました こちら が、彼の理屈は理解できない。正しいのでしょうが 彼がどこから（2/）を得たのか、ぜひ理解したい。 R ² )× r と、最終的な解をどのように導き出すのか。

更新しました。 この質問を投稿してから7年が経ちますが、平方根アルゴリズムの背後にある数学に関する実際の質問について、まだ満足のいく回答が得られていません。そこで、1日かけて自分で答えを書きました。 私の回答へのリンク .

どのように解決するのですか？

半径の円内にランダムな点を生成する方法 R :

r = R * sqrt(random())
theta = random() * 2 * PI

(仮に random() は0と1の間の値を一律に与える)

これを直交座標に変換したい場合は、次のようにします。

x = centerX + r * cos(theta)
y = centerY + r * sin(theta)

なぜ sqrt(random()) ?

に至るまでの計算を見てみましょう。 sqrt(random()) . 簡単のために、単位円を使っていると仮定する。 R = 1.

点間の平均距離は、中心からどれだけ離れても同じになるはずです。つまり、例えば円周率2の円の外周を見た場合、円周率1の円の外周を見た場合の2倍の数の点が見つかるはずである。

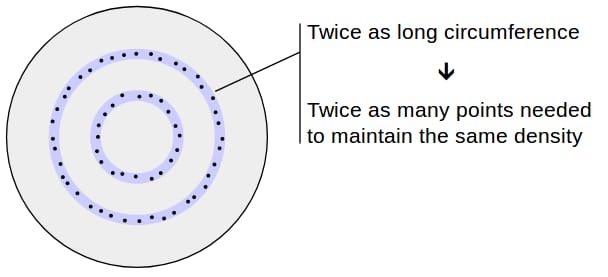
円の円周（2π）なので r に対して直線的に成長する。 r であることから，ランダムポイントの数は r . 言い換えれば 確率密度関数 (PDF)は線形に成長する。PDFは面積が1に等しく、最大半径が1であることが望ましいので、次のようになります。

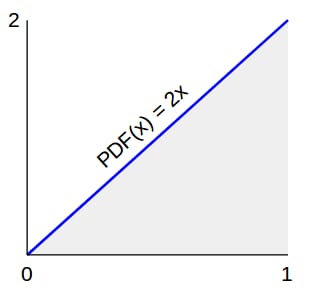
これで、乱数値の密度がどうあるべきかがわかりました。 では 0と1の間の一様な乱数値しかない場合、どのようにしてそのような乱数値を生成するのでしょうか？

というトリックを使います。 逆変換サンプリング

1. PDFから 累積分布関数 (CDF)
2. に沿ってミラーリングします。 y = x
3. 出来上がった関数を0から1の間の一様な値に適用します。

難しそうですか？直感を伝えるちょっとした脇役をブロッククオートに挿入してみましょう。

次のような分布のランダムな点を生成したいとします。

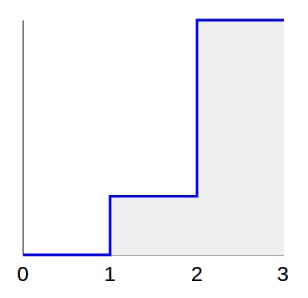
それは

• 1と2の間に一様に1/5の点数、および
• 2と3の間で一様に4/5の点数。

CDFはその名の通り、PDFの累積版である。直感的には PDF( x ) はランダムな値の数を表します。 でx の場合、CDF( x ) は、ランダムな値の数を表します。 xより小さい .

この場合、CDFは次のようになります。

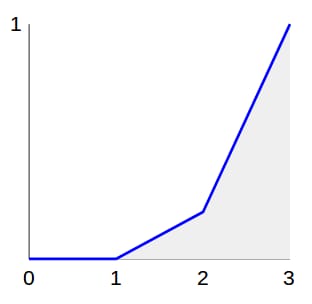
これがどのように役立つかを見るために、左から右へ一様に分布した高さの弾丸を撃つことを想像してください。弾丸は線に当たると、地面に落ちていきます。

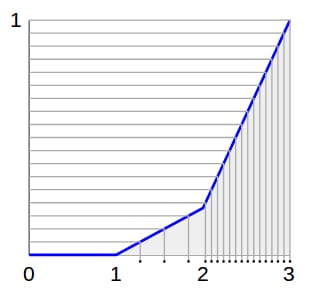
地上の弾丸の密度が、私たちが望む分布と一致しているのをご覧ください。あと少しです!

問題は、この関数の場合 y 軸は 出力 であり x 軸は 入力 . 地面からまっすぐ上にしか弾を撃てないんです。逆関数が必要なんです!

そのため、全体をミラーリングしているのです。 x になります。 y と y になります。 x :

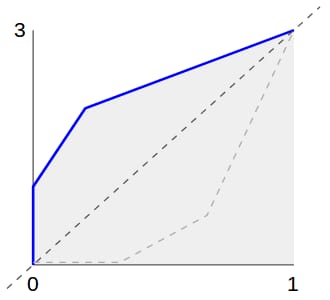
私たちはこれを CDF ^-1 . 目的の分布に従った値を得るために，CDF を利用します ^-1 (random())を使用します。

...そこで、PDFが2になるようにランダムな半径の値を生成することに戻ります。 x .

ステップ1：CDFを作成する．

実数を扱うので、CDFはPDFの積分として表現されます。

CDF ( x ) = ∫ 2 x = x ²

ステップ2：CDFを沿うようにミラーリングする y = x :

数学的に言うと、これは以下のようになります。 x と y を解き y :

CDF :      y = x ²

スワップ    x = y ²

解いてください。    y = √ x

CDF ^-1 :   y = √ x

ステップ3: 得られた関数を0から1の間の一様な値に適用する

CDF ^-1 (random()) = √random()

これが、私たちが導き出そうとしたものです :-)