[解決済み] 円周率の計算が正確かどうかを判断するにはどうしたらよいですか？

質問

円周率の数字を順次与えるプログラムを実装するために、いろいろな方法を試していました。私が試したのは テイラー級数 しかし、収束が非常に遅いことが判明しました（しばらくしてオンラインの値と比較したところ）。とにかく、もっと良いアルゴリズムを試しています。

そこで、プログラムを書いているうちに、すべてのアルゴリズムに共通する問題で行き詰まりました。 n 計算した数字が正確かどうか？

解決方法は？

私は現在、円周率の最多桁数の世界記録保持者なので、私の 2セント :

実際に世界新記録を出すのでなければ、計算した数字を既知の値と照らし合わせるだけというのが一般的なやり方です。だから簡単なことなんです。

実は、計算結果を検証するために、数字の断片を並べたウェブページがあるんです。 http://www.numberworld.org/digits/Pi/

でも、世界記録の領域になると、比較するものがないんですよね。

歴史的に、計算された数字が正しいかどうかを確認するための標準的なアプローチは、2番目のアルゴリズムを使って数字を再計算することです。そのため、どちらかの計算がうまくいかないと、最終的な数字が一致しないのです。

このため、通常、必要な時間は2倍以上になります（2番目のアルゴリズムは通常、より遅いため）。しかし、計算された数字を確認する唯一の方法は、これまでに計算されたことのない数字と世界新記録という未知の領域に踏み込んでしまったときです。

スーパーコンピューターが記録を打ち立てていた時代には、2種類の AGMアルゴリズム がよく使われていました。

• ガウスレジェンドルアルゴリズム
• Borweinのアルゴリズム

これらはいずれも O(N log(N)^2) というアルゴリズムで、かなり簡単に実装することができました。

ところが、今はちょっと事情が違うんです。過去3回の世界記録では、2回の計算を行うのではなく、既知の最速の数式を使って1回だけ計算を行いました( チュドノフスキー式 ):

このアルゴリズムは実装が非常に難しいのですが、AGMアルゴリズムに比べるとかなり高速になります。

次に、2進数の検証を 桁抽出のためのBBP式 .

この式で、任意の2進数を計算することができる を使わずに は、その前の桁をすべて計算します。そこで、最後に計算された2進数の数桁を検証するために使用されます。したがって、これは 大いに 完全な計算よりも高速になります。

という利点があります。

1. 高価な計算が1回で済みます。

デメリットは

1. の実装が必要です。 ベイリー・ボルワイン・プルーフ (BBP)式が必要です。
2. 2進数から10進数への基数変換を確認するための追加手順が必要です。

<サブ なぜ最後の数桁を検証することが、すべての桁が正しいことを意味するのか、詳細は割愛させていただきました。しかし、計算ミスは最後の桁に伝搬するため、このことは容易に理解できる。

さて、この最後のステップ（変換の検証）は、実はかなり重要です。過去の世界記録保持者の一人 実際に私たちに声をかけてくれたのは というのも、当初、私はこの仕組みについて十分な説明をしていなかったからです。

そこで、私のブログからこのスニペットを引っ張ってきました。

N = # of decimal digits desired
p = 64-bit prime number

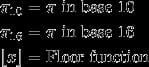
Aを基数10の算術で、Bを2進数の算術で計算しなさい。

もし A = B であれば、極めて高い確率で、変換は正しい。

さらに詳しく知りたい方は、私のブログ記事をご覧ください。 円周率 - 5兆分の1桁 .