[解決済み] πの値を最も早く求める方法は何ですか？

質問

個人的な課題として、πの値を最速で求める方法を探しています。具体的には、以下のものを使わない方法です。 #define のような定数 M_PI または、ハードコーディングで数値を入力します。

以下のプログラムは、私が知っている様々な方法をテストしています。インラインアセンブリ版は、理論的には最も速いオプションですが、明らかにポータブルではありません。他のバージョンと比較するためのベースラインとして、このバージョンを含めました。私のテストでは、ビルトインを使用した場合は 4 * atan(1) バージョンは GCC 4.2 で最速です。 atan(1) を定数に変換します。とは -fno-builtin を指定すると atan2(0, -1) のバージョンが最速です。

以下は、メインのテストプログラム( pitimes.c ):

#include <math.h>
#include <stdio.h>
#include <time.h>

#define ITERS 10000000
#define TESTWITH(x) {                                                       \
    diff = 0.0;                                                             \
    time1 = clock();                                                        \
    for (i = 0; i < ITERS; ++i)                                             \
        diff += (x) - M_PI;                                                 \
    time2 = clock();                                                        \
    printf("%s\t=> %e, time => %f\n", #x, diff, diffclock(time2, time1));   \
}

static inline double
diffclock(clock_t time1, clock_t time0)
{
    return (double) (time1 - time0) / CLOCKS_PER_SEC;
}

int
main()
{
    int i;
    clock_t time1, time2;
    double diff;

    /* Warmup. The atan2 case catches GCC's atan folding (which would
     * optimise the ``4 * atan(1) - M_PI'' to a no-op), if -fno-builtin
     * is not used. */
    TESTWITH(4 * atan(1))
    TESTWITH(4 * atan2(1, 1))

#if defined(__GNUC__) && (defined(__i386__) || defined(__amd64__))
    extern double fldpi();
    TESTWITH(fldpi())
#endif

    /* Actual tests start here. */
    TESTWITH(atan2(0, -1))
    TESTWITH(acos(-1))
    TESTWITH(2 * asin(1))
    TESTWITH(4 * atan2(1, 1))
    TESTWITH(4 * atan(1))

    return 0;
}

そして、インラインアセンブリのもの ( fldpi.c ) これは、x86 と x64 システムでのみ動作します。

double
fldpi()
{
    double pi;
    asm("fldpi" : "=t" (pi));
    return pi;
}

そして、私がテストしているすべてのコンフィギュレーションをビルドするビルドスクリプト ( build.sh ):

#!/bin/sh
gcc -O3 -Wall -c           -m32 -o fldpi-32.o fldpi.c
gcc -O3 -Wall -c           -m64 -o fldpi-64.o fldpi.c

gcc -O3 -Wall -ffast-math  -m32 -o pitimes1-32 pitimes.c fldpi-32.o
gcc -O3 -Wall              -m32 -o pitimes2-32 pitimes.c fldpi-32.o -lm
gcc -O3 -Wall -fno-builtin -m32 -o pitimes3-32 pitimes.c fldpi-32.o -lm
gcc -O3 -Wall -ffast-math  -m64 -o pitimes1-64 pitimes.c fldpi-64.o -lm
gcc -O3 -Wall              -m64 -o pitimes2-64 pitimes.c fldpi-64.o -lm
gcc -O3 -Wall -fno-builtin -m64 -o pitimes3-64 pitimes.c fldpi-64.o -lm

様々なコンパイラ・フラグでテストする以外に（最適化が異なるので、32ビットと64ビットも比較しました）、テストの順番を入れ替えてもみました。しかし、それでも atan2(0, -1) のバージョンが毎回上位を占めています。

解決方法は？

その モンテカルロ法 しかし、最速でないことは明らかです。また、どのような精度を求めるかにもよります。私が知っている最速のπは、桁がハードコードされているものです。以下はその例です。 円周率 と Pi[PDF]の場合 というように、数式がたくさん出てきます。

1回の反復で約14桁という高速で収束する方法を紹介します。 パイファスト 現在、最速のアプリケーションである "FFT "は、この式とFFTを使用しています。コードは簡単なので、式だけ書いておきます。この式は、ほぼ ラマヌジャンが発見し、チェドノフスキーが発見した。 . 実際に彼が数十億桁の数字を計算した方法ですから、無視できる方法ではありません。この式はすぐにオーバーフローしてしまうので、階乗を割っているのだから、このような計算を遅らせて項を削除することが有利になる。

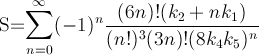
のところです。

以下は ブレント・サラミンアルゴリズム . ウィキペディアには、以下のように書かれています。 a と b が十分に近いとすると (a + b)² / 4t がπの近似値となる。十分近いとはどういうことかわからないが、私のテストでは、1回の反復で2桁、2回で7桁、3回で15桁だった。 真 の計算がより正確になる可能性があります。

let pi_2 iters =
    let rec loop_ a b t p i =
        if i = 0 then a,b,t,p
        else
            let a_n = (a +. b) /. 2.0 
            and b_n = sqrt (a*.b)
            and p_n = 2.0 *. p in
            let t_n = t -. (p *. (a -. a_n) *. (a -. a_n)) in
            loop_ a_n b_n t_n p_n (i - 1)
    in 
    let a,b,t,p = loop_ (1.0) (1.0 /. (sqrt 2.0)) (1.0/.4.0) (1.0) iters in
    (a +. b) *. (a +. b) /. (4.0 *. t)

最後に、円周率ゴルフ（800桁）はいかがでしょうか？160文字！？

int a=10000,b,c=2800,d,e,f[2801],g;main(){for(;b-c;)f[b++]=a/5;for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);}