[解決済み] Python でリストがアイテムを共有しているかどうかをテストする

質問

私は を確認したい。 が別のリストに存在するかどうかを調べたい。 私は以下のコードで簡単にそれを行うことができますが、私はこれを行うためのライブラリ関数があるかもしれないと思います。 そうでない場合は、同じ結果を達成するために、より多くのpythonicメソッドがあります。

In [78]: a = [1, 2, 3, 4, 5]

In [79]: b = [8, 7, 6]

In [80]: c = [8, 7, 6, 5]

In [81]: def lists_overlap(a, b):
   ....:     for i in a:
   ....:         if i in b:
   ....:             return True
   ....:     return False
   ....: 

In [82]: lists_overlap(a, b)
Out[82]: False

In [83]: lists_overlap(a, c)
Out[83]: True

In [84]: def lists_overlap2(a, b):
   ....:     return len(set(a).intersection(set(b))) > 0
   ....: 

どのように解決するのですか？

短い答え 使用方法 not set(a).isdisjoint(b) を使うのが一般的に一番速いです。

2つのリストが a と b は何らかの項目を共有しています。最初の選択肢は、両方をセットに変換して、そのように、それらの交差をチェックすることです。

bool(set(a) & set(b))

なぜなら のセットはPythonのハッシュテーブルを使って保存されるので、それらを検索することは O(1) (を参照してください。 はこちら を参照してください)。理論的には、これは O(n+m) に対して平均的に n と m オブジェクトをリスト a と b . しかし、1) リストからセットを作成する必要があり、無視できない時間がかかる可能性があります。

2番目の方法は、リストの反復処理を行うジェネレータ式を使用することです。

any(i in a for i in b)

これはインプレース検索を可能にし、中間変数に新しいメモリを割り当てないようにします。また、最初の検索でベイルアウトします。 しかし in 演算子は常に O(n) リスト上で (参照 をご覧ください。 ).

もう一つの提案は、ハイブリッドで、リストの一つを繰り返し、もう一つをセットで変換し、このセットのメンバーシップをテストするというものです。

a = set(a); any(i in a for i in b)

四つ目のアプローチは isdisjoint() メソッドを利用することです(凍結された ここで を参照)、例えば

not set(a).isdisjoint(b)

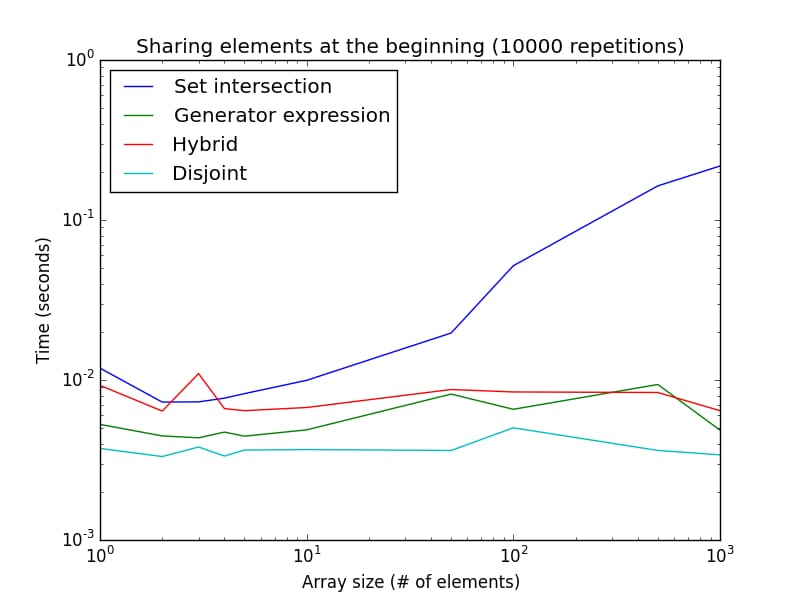
検索する要素が配列の先頭付近にある場合（ソートされているなど）、セットの交差メソッドは中間変数に新しいメモリを割り当てる必要があるため、ジェネレータ式が有利です。

from timeit import timeit
>>> timeit('bool(set(a) & set(b))', setup="a=list(range(1000));b=list(range(1000))", number=100000)
26.077727576019242
>>> timeit('any(i in a for i in b)', setup="a=list(range(1000));b=list(range(1000))", number=100000)
0.16220548999262974

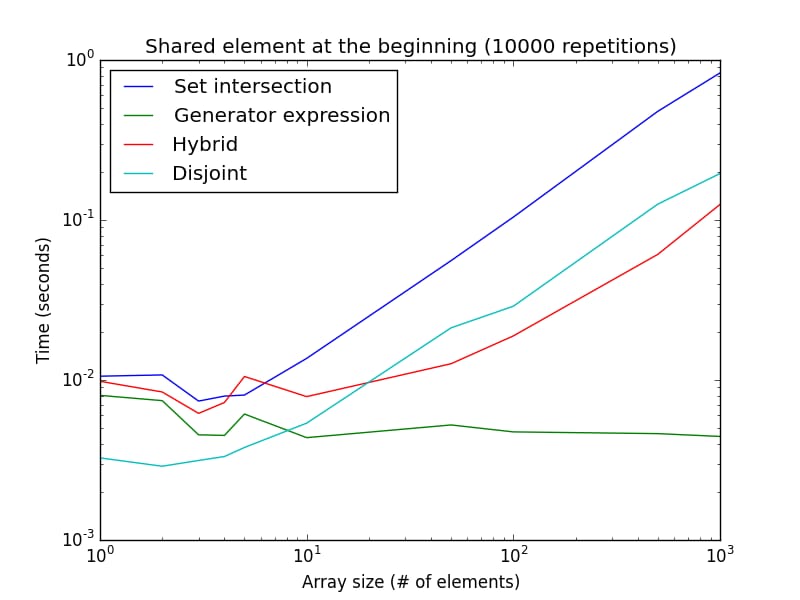
この例の実行時間をリストサイズの関数で表したグラフがこちらです。

両方の軸が対数であることに注意してください。これはジェネレータ式の最良のケースを表しています。見てわかるように isdisjoint() メソッドは非常に小さなリストサイズに適しており、ジェネレータ式は大きなリストサイズに適しています。

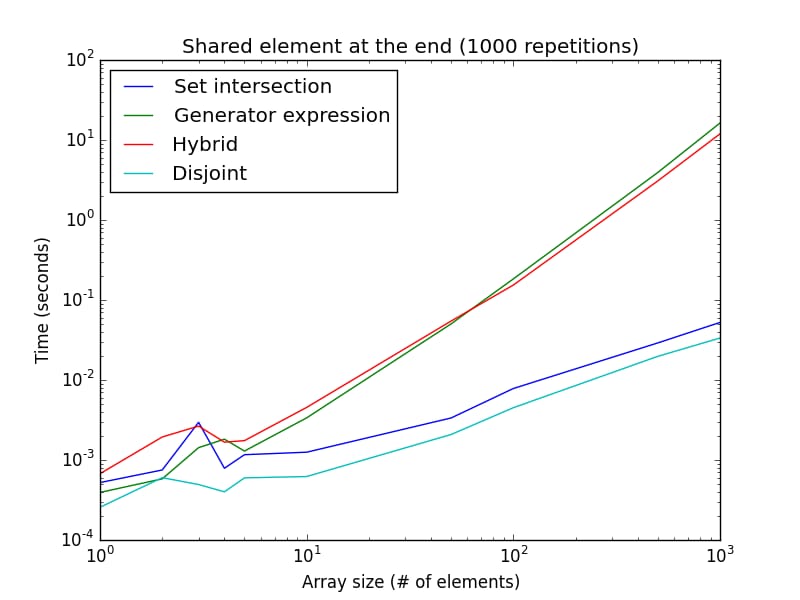
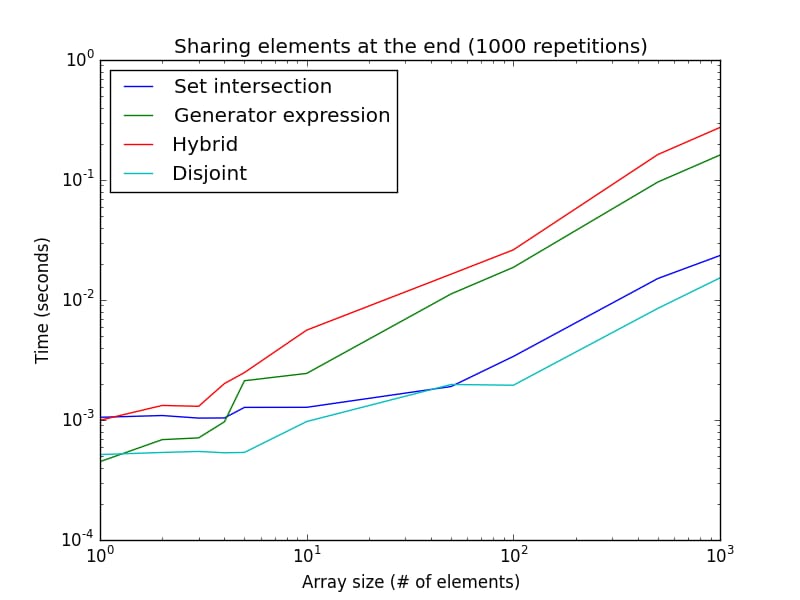
一方、ハイブリッドとジェネレータ式では探索が最初から始まるため、共有要素が体系的に配列の最後にある場合（または両方のリストが値を共有していない場合）、ディスジョイントとセットの交差アプローチはジェネレータ式とハイブリッドアプローチよりずっと速くなります。

>>> timeit('any(i in a for i in b)', setup="a=list(range(1000));b=[x+998 for x in range(999,0,-1)]", number=1000))
13.739536046981812
>>> timeit('bool(set(a) & set(b))', setup="a=list(range(1000));b=[x+998 for x in range(999,0,-1)]", number=1000))
0.08102107048034668

興味深いのは、ジェネレータ式はリストサイズが大きくなると非常に遅くなることです。これは、前の図の100000回の繰り返しではなく、1000回の繰り返しの場合のみです。この設定は、要素が共有されない場合にもよく近似し、不連続および集合交差のアプローチにとって最良のケースとなります。

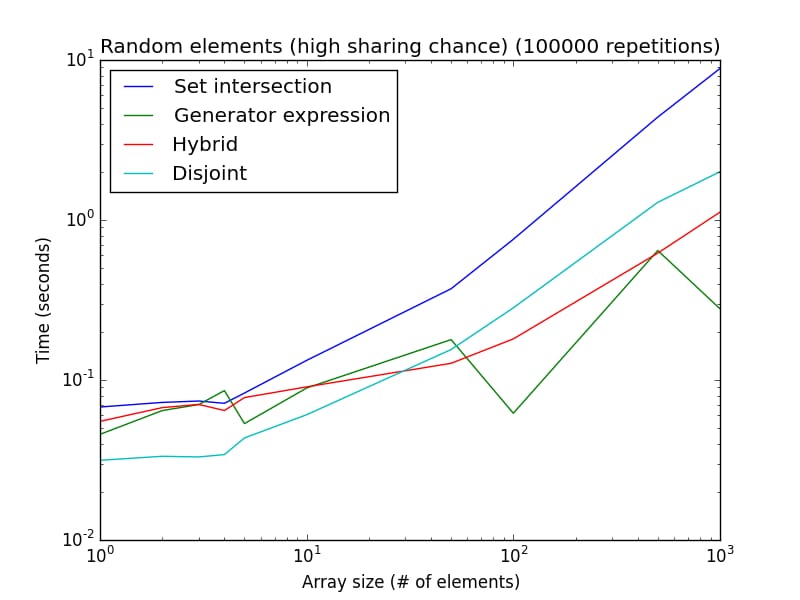
乱数を使用した2つの分析です(1つの手法または別の手法を好むようにセットアップを装備するのではなく)。

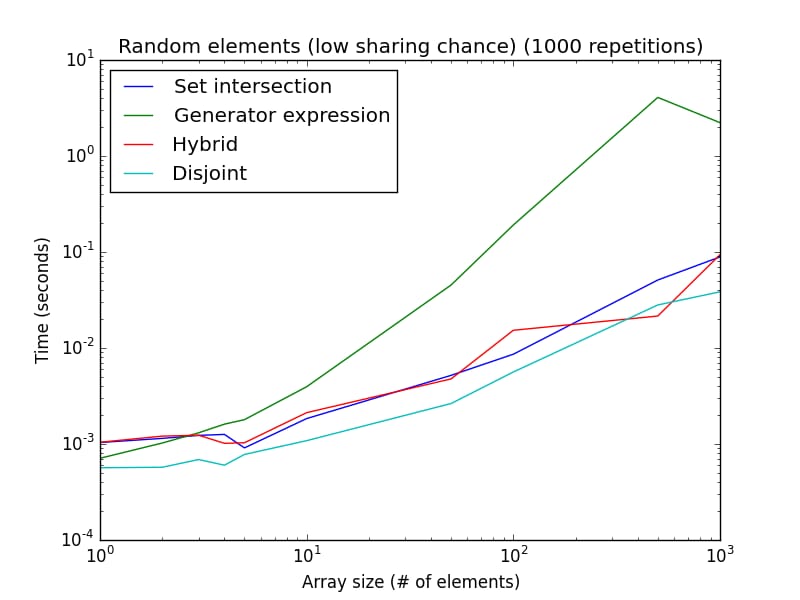
高い確率で共有される: 要素はランダムに [1, 2*len(a)] . 共有される可能性が低い場合: 要素はランダムに [1, 1000*len(a)] .

ここまでの解析では、2つのリストが同じ大きさであることを前提としています。異なるサイズの2つのリスト、例えば a はずっと小さくなります。 isdisjoint() は常に高速です。

を確認します。 a のリストが小さくなっていることを確認してください。そうでない場合はパフォーマンスが低下します。この実験では a のリストサイズを一定にして 5 .

まとめると

• リストが非常に小さい場合(< 10要素)。 not set(a).isdisjoint(b) は常に最速です。
• リストの要素がソートされていたり、利用できる正規の構造を持っている場合、ジェネレータ式である any(i in a for i in b) は大きなリストサイズでは最速です。
• で集合の交差をテストします。 not set(a).isdisjoint(b) よりも常に高速です。 bool(set(a) & set(b)) .
• ハイブリッドな "iterate through list, test on set" a = set(a); any(i in a for i in b) は、一般的に他のメソッドよりも遅いです。
• ジェネレータ式とハイブリッドは、要素を共有しないリストに関しては、他の 2 つのアプローチよりもはるかに遅くなります。

ほとんどの場合 isdisjoint() メソッドを使用することは、要素が共有されていない場合に非常に非効率的であるため、ジェネレータ式の実行にはるかに時間がかかるので、最良のアプローチです。