[解決済み] MATLABによる差分の分割

質問

ニュートンの差分法(遡及版)を行っています。 ここで しかし、この部分に問題があります。

for j=1:n
        for i=n:-1:j
            d(i)=(d(i)-d(i-1))/(x(i)-x(i-j));   
        end

    end

d(0)を使わないでこの処理を始めるには？

これまで試行錯誤してきました。

for j=1:n
    for i=n:-1:j+1
        d(i)=(d(i)-d(i-1))/(x(i)-x(i-j)); 

    end

end

これが助けになることを願っています（私は誰かの検証が必要なだけです）:)。

以下はコード全体です :)

 n=15; 
t=-5:5;
 d=zeros(1,n); 
x=linspace(-5,5,n); 
for i=1:n
>     d(i)=1/(1+x(i)^2); 
end
> 
> for j=1:n
>     for i=n:-1:j+1
>         d(i)=(d(i)-d(i-1))/(x(i)-x(i-j)); 
>             
>     end
>     end
> 
> 
> disp('The coefficients are:') 
disp(d)

私の成績

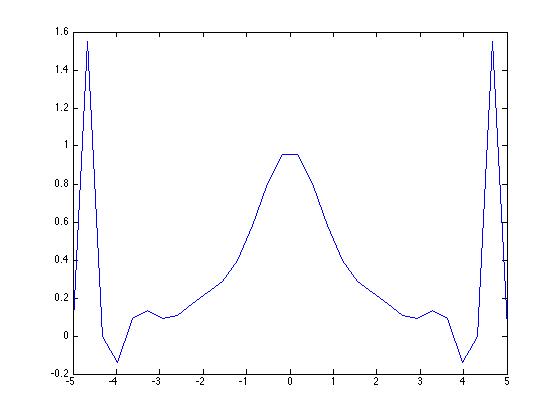
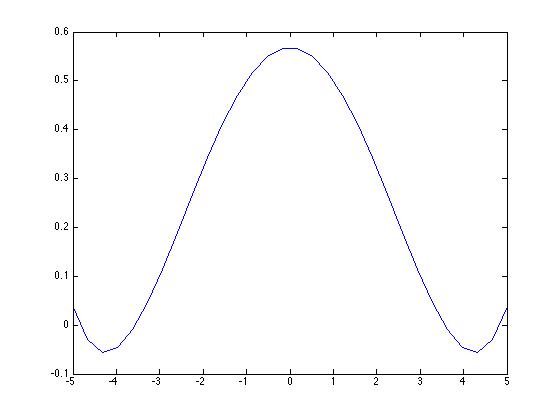
15個の係数を計算すると、次のような多項式になります。

5つの係数を持つ

詳細

補間多項式をプロットしたいので、実際のコード全体はこんな感じです。

n = 15;                    
t = -5:5;
d = zeros(1,n+1);            
x = linspace(-5,5,n+1); 
for i = 1:n+1
     d(i)=1/(1+x(i)^2); 
end

for j = 1:n
    for i = n+1:-1:j+1     
        d(i) = (d(i)-d(i-1))/(x(i)-x(i-j)); 
    end
end


disp('The coefficients are:')
disp(d)



x_1=linspace(-5,5,30);
y_1=d(1)+...
    d(2).*(x_1-x(1))+...
    d(3).*(x_1-x(1)).*(x_1-x(2))+...
    d(4).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3))+...
    d(5).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4))+...
    d(6).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5))+...
    d(7).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6))+...
    d(8).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7))+...
    d(9).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8))+...
    d(10).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9))+...
    d(11).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10))+...
    d(12).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10)).*(x_1-(x(11)))+...
    d(13).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10)).*(x_1-(x(11))).*(x_1-x(12))+...
    d(14).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10)).*(x_1-(x(11))).*(x_1-x(12)).*(x_1-x(13))+...
    d(15).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10)).*(x_1-(x(11))).*(x_1-x(12)).*(x_1-x(13)).*(x_1-x(14))+...
    d(16).*(x_1-x(1)).*(x_1-x(2)).*(x_1-x(3)).*(x_1-x(4)).*(x_1-x(5)).*(x_1-x(6)).*(x_1-x(7)).*(x_1-x(8)).*(x_1-x(9)).*(x_1-x(10)).*(x_1-(x(11))).*(x_1-x(12)).*(x_1-x(13)).*(x_1-x(14)).*(x_1-x(15));    


z_1=1./(1+(x_1).^2);

disp('Our differences are:')
disp(z_1-y_1)
plot(x_1,y_1)

が、これでは非常に不格好なので、多項式 y_1 を for ループに入れたい :)

どのように解決するのですか？

これは非常に一般的なインデックスの問題です。インデックスを1つずらすだけで解決できます。このとき、d(1)は以前のd(0)であることを覚えておく必要があります（数学のテキストで見るd(0)と同じです）。数学は同じで、インデックスが違うだけです。

n = 15;                    
t = -5:5;
d = zeros(1,n+1);          % Give d one more element. The math notation d(0):d(15) will be equivalent to d(1):d(16) here.   
x = linspace(-5,5,n+1); 
for i = 1:n+1
     d(i)=1/(1+x(i)^2); 
end

for j = 1:n
    for i = n+1:-1:j+1     % Also shift i by 1 because you use this to index d.
        d(i) = (d(i)-d(i-1))/(x(i)-x(i-j)); 
    end
end

これはあくまでインデックス問題を回避する方法を示すための例です。数学的な妥当性はご自身で検証してください。

コードの最後の部分は、再帰的な関数呼び出しを使用することができます。

function y = ff(ii)
if ii > 0
    y = ff(ii-1) + d(ii+1).*(x_1-x(ii));
else
    y = d(1);
end
end

ii = 1の時に分かると思います。

y = ff(1) = ff(0) + d(2).*(x_1-x(1)) = d(1) + d(2).*(x_1-x(1));

で、ii = 2のとき。

y = ff(2) = ff(1) + d(3).*(x_1-x(2)) = d(1) + d(2).*(x_1-x(1)) + d(3).*(x_1-x(2))

などなど...