[解決済み] ある行列から固有ベクトルの異なる解を得ることができるでしょうか？

質問

ある行列の固有ベクトルを求めることが目的です。Matlabでは [V,D] = eig(M) を使って、行列の固有ベクトルを求める。 [V,D] = eig(M) . または、ウェブサイトを利用しました。 ウルフラムアルファ を使い、結果を再確認しました。

私たちは 10X10 という行列があります。 M :

0.736538062307847   -0.638137874226607  -0.409041107160722  -0.221115060391256  -0.947102932298308  0.0307937582853794  1.23891356582639    1.23213871779652    0.763885436104244   -0.805948245321096
-1.00495215920171   -0.563583317483057  -0.250162608745252  0.0837145788064272  -0.201241986127792  -0.0351472158148094 -1.36303599752928   0.00983020375259212 -0.627205458137858  0.415060573134481
0.372470672825535   -0.356014310976260  -0.331871925811400  0.151334279460039   0.0983275066581362  -0.0189726910991071 0.0261595600177302  -0.752014960080128  -0.00643718050231003    0.802097123260581
1.26898635468390    -0.444779390923673  0.524988731629985   0.908008064819586   -1.66569084499144   -0.197045800083481  1.04250295411159    -0.826891197039745  2.22636770820512    0.226979917020922
-0.307384714237346  0.00930402052877782 0.213893752473805   -1.05326116146192   -0.487883985126739  0.0237598951768898  -0.224080566774865  0.153775526014521   -1.93899137944122   -0.300158630162419
7.04441299430365    -1.34338456640793   -0.461083493351887  5.30708311554706    -3.82919170270243   -2.18976040860706   6.38272280044908    2.33331906669527    9.21369926457948    -2.11599193328696
1   0   0   0   0   0   0   0   0   0
0   1   0   0   0   0   0   0   0   0
0   0   0   1   0   0   0   0   0   0
0   0   0   0   0   0   1   0   0   0

D :

2.84950796497613 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    1.08333535157800 + 0.971374792725758i   0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    1.08333535157800 - 0.971374792725758i   0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -2.05253164206377 + 0.00000000000000i   0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -0.931513274011512 + 0.883950434279189i 0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -0.931513274011512 - 0.883950434279189i 0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -1.41036956613286 + 0.354930202789307i  0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -1.41036956613286 - 0.354930202789307i  0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    -0.374014257422547 + 0.00000000000000i  0.00000000000000 + 0.00000000000000i
0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.00000000000000 + 0.00000000000000i    0.165579401742139 + 0.00000000000000i

V :

-0.118788118233448 + 0.00000000000000i  0.458452024790792 + 0.00000000000000i   0.458452024790792 + -0.00000000000000i  -0.00893883603500744 + 0.00000000000000i    -0.343151745490688 - 0.0619235203325516i    -0.343151745490688 + 0.0619235203325516i    -0.415371644459693 + 0.00000000000000i  -0.415371644459693 + -0.00000000000000i -0.0432672840354827 + 0.00000000000000i 0.0205670999343567 + 0.00000000000000i
0.0644460666316380 + 0.00000000000000i  -0.257319460426423 + 0.297135138351391i -0.257319460426423 - 0.297135138351391i 0.000668740843331284 + 0.00000000000000i    -0.240349418297316 + 0.162117384568559i -0.240349418297316 - 0.162117384568559i -0.101240986260631 + 0.370051721507625i -0.101240986260631 - 0.370051721507625i 0.182133003667802 + 0.00000000000000i   0.0870047828436781 + 0.00000000000000i
-0.0349638967773464 + 0.00000000000000i -0.0481533171088709 - 0.333551383088345i    -0.0481533171088709 + 0.333551383088345i    -5.00304864960391e-05 + 0.00000000000000i   -0.0491721720673945 + 0.235973015480054i    -0.0491721720673945 - 0.235973015480054i    0.305000451960374 + 0.180389787086258i  0.305000451960374 - 0.180389787086258i  -0.766686233364027 + 0.00000000000000i  0.368055402163444 + 0.00000000000000i
-0.328483258287378 + 0.00000000000000i  -0.321235466934363 - 0.0865401147007471i    -0.321235466934363 + 0.0865401147007471i    -0.0942807049530764 + 0.00000000000000i -0.0354015249204485 + 0.395526630779543i    -0.0354015249204485 - 0.395526630779543i    -0.0584777280581259 - 0.342389123727367i    -0.0584777280581259 + 0.342389123727367i    0.0341847135233905 + 0.00000000000000i  -0.00637190625187862 + 0.00000000000000i
0.178211880664383 + 0.00000000000000i   0.236391683569043 - 0.159628238798322i  0.236391683569043 + 0.159628238798322i  0.00705341924756006 + 0.00000000000000i 0.208292766328178 + 0.256171148954103i  0.208292766328178 - 0.256171148954103i  -0.319285221542254 - 0.0313551221105837i    -0.319285221542254 + 0.0313551221105837i    -0.143900055026164 + 0.00000000000000i  -0.0269550068563120 + 0.00000000000000i
-0.908350536903352 + 0.00000000000000i  0.208752559894992 + 0.121276611951418i  0.208752559894992 - 0.121276611951418i  -0.994408141243082 + 0.00000000000000i  0.452243212306010 + 0.00000000000000i   0.452243212306010 + -0.00000000000000i  0.273997199582534 - 0.0964058973906923i 0.273997199582534 + 0.0964058973906923i -0.0270087356931836 + 0.00000000000000i 0.00197408431000798 + 0.00000000000000i
-0.0416872385315279 + 0.00000000000000i 0.234583850413183 - 0.210340074973091i  0.234583850413183 + 0.210340074973091i  0.00435502958971167 + 0.00000000000000i 0.160642433241717 + 0.218916331789935i  0.160642433241717 - 0.218916331789935i  0.276971588308683 + 0.0697020017773242i 0.276971588308683 - 0.0697020017773242i 0.115683515205146 + 0.00000000000000i   0.124212913671392 + 0.00000000000000i
0.0226165595687948 + 0.00000000000000i  0.00466011130798999 + 0.270099580217056i    0.00466011130798999 - 0.270099580217056i    -0.000325812684017280 + 0.00000000000000i   0.222664282388928 + 0.0372585184944646i 0.222664282388928 - 0.0372585184944646i 0.129604953142137 - 0.229763189016417i  0.129604953142137 + 0.229763189016417i  -0.486968076893485 + 0.00000000000000i  0.525456559984271 + 0.00000000000000i
-0.115277185508808 + 0.00000000000000i  -0.204076984892299 + 0.103102999488027i -0.204076984892299 - 0.103102999488027i 0.0459338618810664 + 0.00000000000000i  0.232009172507840 - 0.204443701767505i  0.232009172507840 + 0.204443701767505i  -0.0184618718969471 + 0.238119465887194i    -0.0184618718969471 - 0.238119465887194i    -0.0913994930540061 + 0.00000000000000i -0.0384824814248494 + 0.00000000000000i
-0.0146296269545178 + 0.00000000000000i 0.0235283849818557 - 0.215256480570249i 0.0235283849818557 + 0.215256480570249i -0.00212178438590738 + 0.00000000000000i    0.0266030060993678 - 0.209766836873709i 0.0266030060993678 + 0.209766836873709i -0.172989400304240 - 0.0929551855455724i    -0.172989400304240 + 0.0929551855455724i    -0.309302420721495 + 0.00000000000000i  0.750171291624984 + 0.00000000000000i

以下のような結果を得ました。

1. オリジナルのマトリクス。

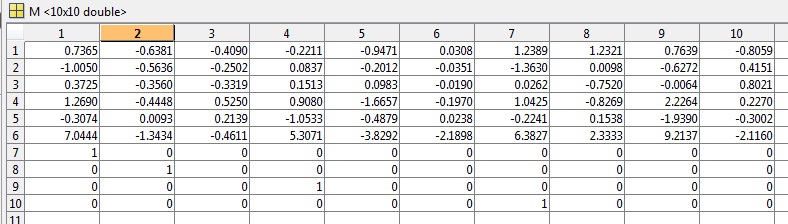
1. WolframAlphaの結果です。

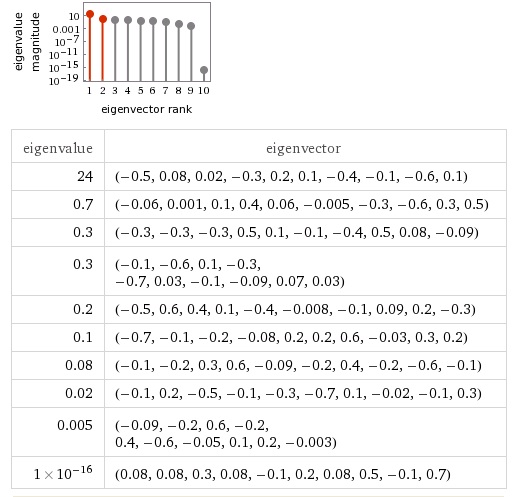
1. Matlab Eigの結果です。

D(固有値)

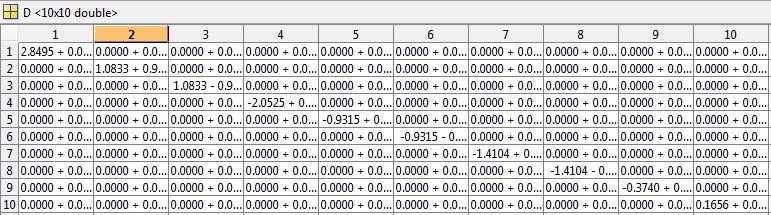
V(固有ベクトル)

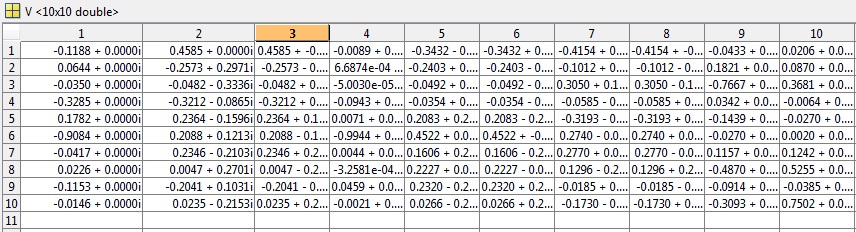
固有ベクトルについて、異なる解を得ることは可能でしょうか、それとも一意な答えであるべきでしょうか。この概念を明確にしたいと思っています。

どのように解決するのですか？

様々な理由により、固有ベクトルは一意ではありません。符号を変えても、同じ固有値に対する固有ベクトルは固有ベクトルのままです。実際、任意の定数を乗じても、固有ベクトルはその定数のままです。ツールによっては、異なる正規化が選択されることもあります。

固有値の多重度が1より大きい場合、固有ベクトルは同じ部分空間にまたがる限り、やはり一意ではありません。