[解決済み] 矩形の集合を重ならないようにカバーするための最小の矩形を求めるアルゴリズム

質問

矩形の集合があり、元の集合と同じ面積を表現するために矩形の数が最も少なくなるように集合を "縮小" したいです。できれば高速に処理したいのですが、それよりも矩形の数をできるだけ少なくすることに関心があります。私は今、ほとんどの場合うまくいくアプローチを持っています。

現在、私は最も左上の矩形から始めて、矩形を維持したまま右と下に拡大できるかどうかを確認しています。拡大できなくなるまでそれを行い、交差するすべての矩形を削除して分割し、拡大した矩形をリストに追加します。そして、次の左上の矩形で再びこのプロセスを開始し、以下同様です。しかし、場合によってはうまくいかないこともあります。たとえば

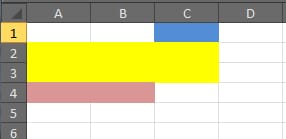
この3つの長方形のセットでは、正しい解答は次のように2つの長方形で終わります。

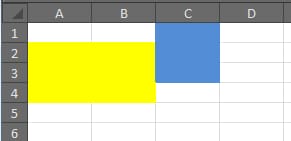
しかし、この場合、私のアルゴリズムは青い長方形を処理することから始まります。これは下方に展開し、黄色の長方形を分割します (正しい)。しかし、その後、黄色の長方形の残りが処理されると、下方に拡大するのではなく、最初に右に拡大し、以前に分割された部分を取り込みます。そして最後の矩形が処理されると、右にも下にも展開できないので、元の矩形の集合が残されます。アルゴリズムを微調整して、まず下に展開し、次に右に展開するようにすることは可能です。そうすればこのケースは解決しますが、反転された同様のシナリオで同じ問題が発生します。

編集してください。 はっきり言って、元の矩形の集合は重ならず、つながっている必要もない。そして、長方形のサブセットが接続されている場合、それらを完全にカバーする多角形は、穴を持つことができます。

どのように解決するのですか？

質問のタイトルとは裏腹に、実際には最小限の 離散 を探しているのだと思います。(Jasonのリンクは、最小の をカバーする に関するもので、これはまったく異なる問題です)。

David Eppstein は、2010年の調査記事の第3節で、この問題を論じています。 計算幾何学問題に対するグラフ理論的解決法 また、彼は以下の記事で素晴らしい要約をしています。 mathoverflow.netのこの回答 :

2つの凹の頂点を端点とする軸平行対角線の最大数を求め、それに沿って分割し、残りの凹の頂点ごとにさらに1つの分割を行うというものです。このグラフは2部構成なので、その最大独立集合はグラフマッチング技術により多項式時間で求めることができる。

Eppsteinの論文から図2を使って、この見事なまでに簡潔な記述について、私の考えを述べます。長方形の多角形があり、おそらく穴があるとします。

多角形を長方形に分解したとき、凹の頂点はそれぞれ分解の少なくとも1つの辺で満たされなければならない。そこで、以下のようになる。 最小 つまり、凹んだ頂点のうちの2つを結ぶ縁ができるだけ多くあれば、最小の断面が得られます。

そこで、ポリゴン内に完全に含まれる2つの凹んだ頂点の間の軸平行な対角線を描いてみましょう。(「軸平行」とは、ここでは「水平または垂直」という意味であって ポリゴンの対角線 は隣接しない2つの頂点を結ぶ線である)。これらの線は、交差しない限り、できるだけ多く解剖に使用したい。

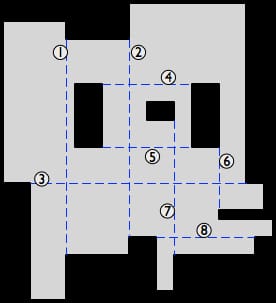
(軸と平行な対角線がない場合は、各凹の頂点から切り取るだけなので、解剖は些細なことである。あるいは、軸と平行な対角線の間に交点がない場合は、それらすべてを使用し、さらに残りの各凹の頂点から切り込みを入れます。そうでなければ、続きを読んでください)。

その 交差点グラフ は、線分ごとにノードがあり、線分が交差する場合は2つのノードを結ぶエッジがあります。以下は、軸と平行な対角線の交点グラフです。

それは 二部作 で、縦の対角線は一方の部分にあり、横の対角線はもう一方の部分にあります。ここで、対角線が交差しない範囲で、できるだけ多くの対角線を選びたい。これは 最大独立集合 を見つけることに相当します。

一般的なグラフで最大独立集合を求めるのはNP困難な問題ですが、2部グラフの特殊なケースで ケーニッヒの定理 によって、最大マッチングを求める問題と等価であることが示され、これは例えば多項式時間で解くことができる。 ホップクロフト-カープアルゴリズム . 与えられたグラフはいくつかの最大マッチングを持つことができますが、それらはすべて同じ大きさなので、どれでもかまいません。この例では、すべての最大マッチングは3組の頂点を持ち、例えば {(2, 4), (6, 3), (7, 8)} のようなものです。

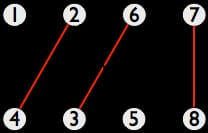
(このグラフの他の最大マッチングには、{(1, 3), (2, 5), (7, 8)}; {(2, 4), (3, 6), (5, 7)}; および {(1, 3), (2, 4), (7, 8)}があります).

最大マッチングから、対応する 最小頂点カバー を適用します。 ケーニッヒの定理の証明 . 上のマッチングでは、左の集合は L  = {1, 2, 6, 7}, 右の集合は R  = {3, 4, 5, 8} であり、一致しない頂点の集合は L は U  = {1}. で始まる交互経路は1つだけである。 U から始まる交互経路は1-3-6だけなので、交互経路の頂点の集合は Z  = {1, 3, 6}であり、最小頂点被覆は次のようになります。 K = ( L  \  Z ) ∪ ( R  ∩  Z ) = {2, 3, 7}で、下の赤で示され、最大の独立集合は緑で示されています。

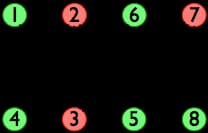
これを解剖の問題に置き換えると、解剖では軸と平行な対角線を5本使えることになります。

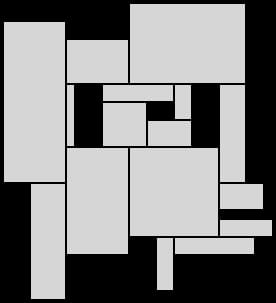
最後に、残った凹の頂点からそれぞれ切り込みを入れ、解体を完了します。