[解決済み] 重なり合う矩形に間隔をあけるアルゴリズム？

質問

この問題は、実際にはロールオーバーを扱っているのですが、以下は一般論として説明します。

私は 2D ビューを持っており、画面上の領域内にいくつかの矩形があります。これらのボックスが互いに重ならず、最小限の移動で調整できるようにするには、どうすればよいでしょうか。

矩形の位置は動的で、ユーザーの入力に依存するため、その位置はどこでもかまいません。

付属の 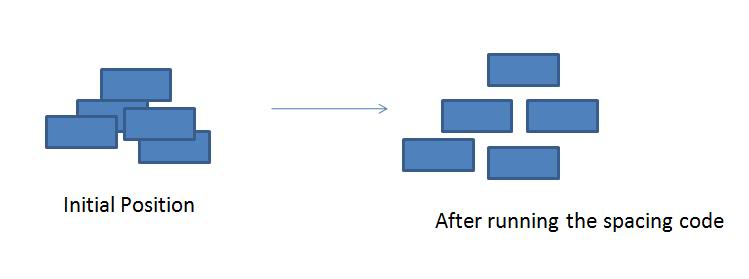の画像は、問題と望ましい解決策を示しています。

現実の問題は、実はロールオーバーを扱っているのです。

コメントでの質問に対する回答

1. 矩形の大きさは固定ではなく、ロールオーバーのテキストの長さに依存する

2. 画面のサイズについてですが、今は画面のサイズがレクタングルに十分であると仮定する方が良いと思います。もし矩形が多すぎて、アルゴが解決策を出せない場合は、コンテンツを調整するしかありません。

3. 最小限の動き」という要件は、絶対的な工学的要件というよりも、美学のためのものです。2 つの長方形の間に広大な距離を追加することによって、間隔を空けることができますが、GUI の一部として見栄えはよくありません。このアイデアは、ロールオーバー/矩形をそのソースにできるだけ近づけることです（その後、ソースに黒い線で接続します）。ですから、「x のために 1 つだけ動かす」または「x の半分のために両方動かす」のどちらでもかまいません。

どのように解決するのですか？

私も同じようなものが必要だったので、これに少し取り組んでいたのですが、アルゴリズムの開発が遅れていました。あなたのおかげで衝動にかられることができました :D

ソースコードも必要だったので、ここにあります。 私は Mathematica で作業しましたが、関数的な機能はあまり使っていないので、どんな手続き型言語にも簡単に翻訳できると思います。

歴史的な視点

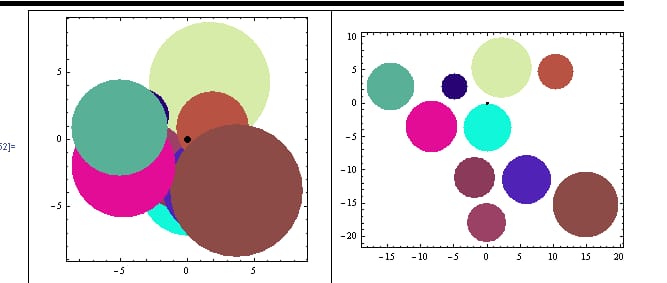
まず、交差点の計算が簡単なので、円のアルゴリズムを開発することにしました。それは、中心と半径に依存するだけです。

Mathematica の方程式ソルバーを使うことができ、うまく実行できました。

見てください。

簡単でした。次のような問題でソルバーを読み込んだだけです。

For each circle
 Solve[
  Find new coördinates for the circle
  Minimizing the distance to the geometric center of the image
  Taking in account that
      Distance between centers > R1+R2 *for all other circles
      Move the circle in a line between its center and the 
                                         geometric center of the drawing
   ]

このように簡単で，Mathematica がすべての作業を行いました．

私は「ハッ！簡単だ！今度は長方形にしよう！」と言いました．しかし私は間違っていました．

長方形のブルース

矩形の主な問題は、交差点のクエリが厄介な関数であることです。以下のようなものです。

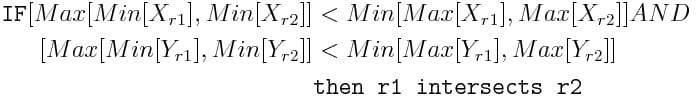
そこで、このような方程式の条件をたくさん入れてMathematicaに与えてみたところ、あまりにパフォーマンスが悪かったので、手続き的なことをすることにしたのです。

私のアルゴリズムは以下のようになりました。

Expand each rectangle size by a few points to get gaps in final configuration
While There are intersections
    sort list of rectangles by number of intersections
    push most intersected rectangle on stack, and remove it from list
// Now all remaining rectangles doesn't intersect each other
While stack not empty
    pop  rectangle from stack and re-insert it into list
    find the geometric center G of the chart (each time!)
    find the movement vector M (from G to rectangle center)
    move the rectangle incrementally in the direction of M (both sides) 
                                                 until no intersections  
Shrink the rectangles to its original size

最小の移動」という条件が完全に満たされていないことにお気づきでしょう (一方向のみ)。しかし、この条件を満たすために矩形をあらゆる方向に移動させると、ユーザーが混乱するようなマップ変更になることがあることがわかりました。

私はユーザーインターフェイスをデザインしているので、長方形を少し遠くに移動させることを選択しましたが、より予測しやすい方法です。空の場所が見つかるまで、現在の位置を囲むすべての角度とすべての半径を検査するようにアルゴリズムを変更することができますが、より多くの要求が出されるでしょう。

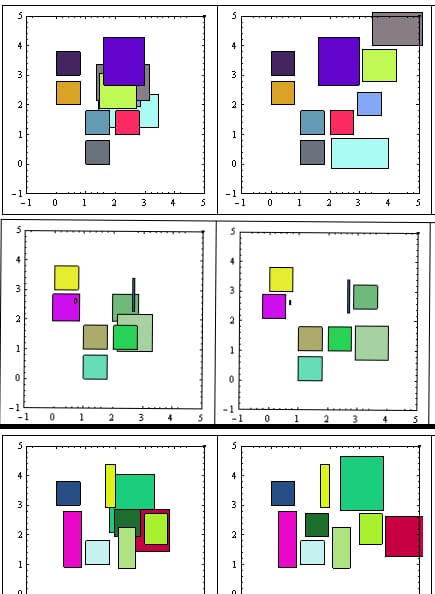
とにかく、これらは結果の例です (前/後)。

編集; その他の例 ここで

ご覧のように、「最小の動き」を満たすことはできませんが、十分な結果が得られています。

私のSVNリポジトリに問題があるため、ここにコードを掲載します。問題が解決したら削除します。

編集してください。

また R-ツリー を使うこともできますが、少数の矩形を扱うにはやりすぎのような気がします。そして、私はそのアルゴリズムをすでに実装していません。おそらく他の誰かが、あなたの選んだプラットフォームでの既存の実装を示すことができるでしょう。

警告! コードは最初のアプローチであり、まだ素晴らしい品質ではありませんし、きっといくつかのバグがあります。

Mathematicaです。

(*Define some functions first*)

Clear["Global`*"];
rn[x_] := RandomReal[{0, x}];
rnR[x_] := RandomReal[{1, x}];
rndCol[] := RGBColor[rn[1], rn[1], rn[1]];

minX[l_, i_] := l[[i]][[1]][[1]]; (*just for easy reading*)
maxX[l_, i_] := l[[i]][[1]][[2]];
minY[l_, i_] := l[[i]][[2]][[1]];
maxY[l_, i_] := l[[i]][[2]][[2]];
color[l_, i_]:= l[[i]][[3]];

intersectsQ[l_, i_, j_] := (* l list, (i,j) indexes, 
                              list={{x1,x2},{y1,y2}} *) 
                           (*A rect does intesect with itself*)
          If[Max[minX[l, i], minX[l, j]] < Min[maxX[l, i], maxX[l, j]] &&
             Max[minY[l, i], minY[l, j]] < Min[maxY[l, i], maxY[l, j]], 
                                                           True,False];

(* Number of Intersects for a Rectangle *)
(* With i as index*)
countIntersects[l_, i_] := 
          Count[Table[intersectsQ[l, i, j], {j, 1, Length[l]}], True]-1;

(*And With r as rectangle *)
countIntersectsR[l_, r_] := (
    Return[Count[Table[intersectsQ[Append[l, r], Length[l] + 1, j], 
                       {j, 1, Length[l] + 1}], True] - 2];)

(* Get the maximum intersections for all rectangles*)
findMaxIntesections[l_] := Max[Table[countIntersects[l, i], 
                                       {i, 1, Length[l]}]];

(* Get the rectangle center *)
rectCenter[l_, i_] := {1/2 (maxX[l, i] + minX[l, i] ), 
                       1/2 (maxY[l, i] + minY[l, i] )};

(* Get the Geom center of the whole figure (list), to move aesthetically*)
geometryCenter[l_] :=  (* returs {x,y} *)
                      Mean[Table[rectCenter[l, i], {i, Length[l]}]]; 

(* Increment or decr. size of all rects by a bit (put/remove borders)*)
changeSize[l_, incr_] :=
                 Table[{{minX[l, i] - incr, maxX[l, i] + incr},
                        {minY[l, i] - incr, maxY[l, i] + incr},
                        color[l, i]},
                        {i, Length[l]}];

sortListByIntersections[l_] := (* Order list by most intersecting Rects*)
        Module[{a, b}, 
               a = MapIndexed[{countIntersectsR[l, #1], #2} &, l];
               b = SortBy[a, -#[[1]] &];
               Return[Table[l[[b[[i]][[2]][[1]]]], {i, Length[b]}]];
        ];

(* Utility Functions*)
deb[x_] := (Print["--------"]; Print[x]; Print["---------"];)(* for debug *)
tableForPlot[l_] := (*for plotting*)
                Table[{color[l, i], Rectangle[{minX[l, i], minY[l, i]},
                {maxX[l, i], maxY[l, i]}]}, {i, Length[l]}];

genList[nonOverlap_, Overlap_] :=    (* Generate initial lists of rects*)
      Module[{alist, blist, a, b}, 
          (alist = (* Generate non overlapping - Tabuloid *)
                Table[{{Mod[i, 3], Mod[i, 3] + .8}, 
                       {Mod[i, 4], Mod[i, 4] + .8},  
                       rndCol[]}, {i, nonOverlap}];
           blist = (* Random overlapping *)
                Table[{{a = rnR[3], a + rnR[2]}, {b = rnR[3], b + rnR[2]}, 
                      rndCol[]}, {Overlap}];
           Return[Join[alist, blist] (* Join both *)];)
      ];

メイン

clist = genList[6, 4]; (* Generate a mix fixed & random set *)

incr = 0.05; (* may be some heuristics needed to determine best increment*)

clist = changeSize[clist,incr]; (* expand rects so that borders does not 
                                                         touch each other*)

(* Now remove all intercepting rectangles until no more intersections *)

workList = {}; (* the stack*)

While[findMaxIntesections[clist] > 0,          
                                      (*Iterate until no intersections *)
    clist    = sortListByIntersections[clist]; 
                                      (*Put the most intersected first*)
    PrependTo[workList, First[clist]];         
                                      (* Push workList with intersected *)
    clist    = Delete[clist, 1];      (* and Drop it from clist *)
];

(* There are no intersections now, lets pop the stack*)

While [workList != {},

    PrependTo[clist, First[workList]];       
                                 (*Push first element in front of clist*)
    workList = Delete[workList, 1];          
                                 (* and Drop it from worklist *)

    toMoveIndex = 1;                        
                                 (*Will move the most intersected Rect*)
    g = geometryCenter[clist];               
                                 (*so the geom. perception is preserved*)
    vectorToMove = rectCenter[clist, toMoveIndex] - g;
    If [Norm[vectorToMove] < 0.01, vectorToMove = {1,1}]; (*just in case*)  
    vectorToMove = vectorToMove/Norm[vectorToMove];      
                                            (*to manage step size wisely*)

    (*Now iterate finding minimum move first one way, then the other*)

    i = 1; (*movement quantity*)

    While[countIntersects[clist, toMoveIndex] != 0, 
                                           (*If the Rect still intersects*)
                                           (*move it alternating ways (-1)^n *)

      clist[[toMoveIndex]][[1]] += (-1)^i i incr vectorToMove[[1]];(*X coords*)
      clist[[toMoveIndex]][[2]] += (-1)^i i incr vectorToMove[[2]];(*Y coords*)

            i++;
    ];
];
clist = changeSize[clist, -incr](* restore original sizes*);

HTH!

編集：マルチアングル検索

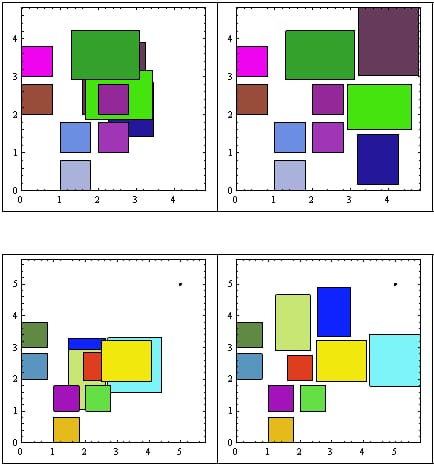
全方向の検索を可能にするアルゴリズムの変更を実装しましたが、幾何学的対称性によって課せられた軸を優先しています。

より多くのサイクルを犠牲にして、これは以下のように、よりコンパクトな最終的な構成になりました。

その他のサンプル こちら .

メインループの擬似コードは、次のように変更されました。

Expand each rectangle size by a few points to get gaps in final configuration
While There are intersections
    sort list of rectangles by number of intersections
    push most intersected rectangle on stack, and remove it from list
// Now all remaining rectangles doesn't intersect each other
While stack not empty
    find the geometric center G of the chart (each time!)
    find the PREFERRED movement vector M (from G to rectangle center)
    pop  rectangle from stack 
    With the rectangle
         While there are intersections (list+rectangle)
              For increasing movement modulus
                 For increasing angle (0, Pi/4)
                    rotate vector M expanding the angle alongside M
                    (* angle, -angle, Pi + angle, Pi-angle*)
                    re-position the rectangle accorging to M
    Re-insert modified vector into list
Shrink the rectangles to its original size

簡潔さのためにソースコードは載せていませんが、使えそうなら頼めばいいだけです。この方法で行くなら、R-treeに切り替えた方が良いと思います（ここでは多くのインターバルテストが必要です）。