[解決済み] Rのユニルート解

質問

次の関数の根を求めたい。

       x=0.5
       f <- function(y) ((1-pbeta(1-exp(-0.002926543
        *( 107.2592+y)^1.082618 *exp(0.04097536*(107.2592+y))),shape1=0.2640229,shape2=0.1595841)) -
(1-pbeta(1-exp(-0.002926543*(x)^1.082618 *exp(0.04097536*(x))),shape1=0.2640229,shape2=0.1595841))^2)

sroot=uniroot(f, lower=0, upper=1000)$root

エラー in uniroot(f, lower = 0, upper = 1000) : 終了時の f() の値 の点が逆符号になっていない

どうすればこのエラーを解決できますか？

どのように解決するのですか？

uniroot() と使用上の注意

uniroot が実装されているのは、粗悪な 二等分法 . このような方法は，以下のように非常に単純です． (準）ニュートン法 しかし、根が存在することを保証するために、より強い仮定が必要です。 f(lower) * f(upper) < 0 .

このような仮定は十分条件ではあっても必要条件ではないので、かなり面倒なことになります。実際には、もし f(lower) * f(upper) > 0 しかし、これは100％確実ではないので、二等分法はそのリスクを負うことができません。

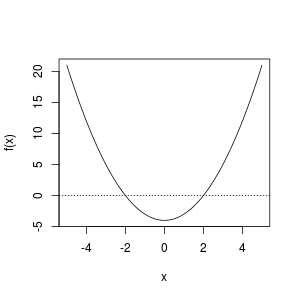
この例で考えてみましょう。

# a quadratic polynomial with root: -2 and 2
f <- function (x) x ^ 2 - 4

明らかに [-5, 5] . しかし

uniroot(f, lower = -5, upper = 5)
#Error in uniroot(f, lower = -5, upper = 5) : 
#  f() values at end points not of opposite sign

実際には、二等分法の使用には、次のような観察／検査が必要です。 f そのため、ルートが存在する妥当な区間を提案することができます。Rでは curve() :

curve(f, from = -5, to = 5); abline(h = 0, lty = 3)

プロットから、ルートが存在するのは [-5, 0] または [0, 5] . なので、これらは問題なく動作します。

uniroot(f, lower = -5, upper = 0)
uniroot(f, lower = 0, upper = 5)

あなたの問題

では、あなたの作った関数を試してみましょう（読みやすくするために何行かに分けています。また、このようにすると正しさを確認しやすくなります）。

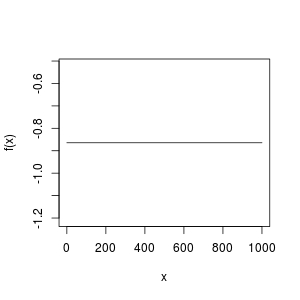
f <- function(y) {
  g <- function (u) 1 - exp(-0.002926543 * u^1.082618 * exp(0.04097536 * u))
  a <- 1 - pbeta(g(107.2592+y), 0.2640229, 0.1595841)
  b <- 1 - pbeta(g(x), 0.2640229, 0.1595841)
  a - b^2
  }

x <- 0.5
curve(f, from = 0, to = 1000)

この関数が水平線であるわけがない。ルートがあるわけがない

1. を確認します。 f 上記は、本当にあなたが望む正しいことをしているのでしょうか？何かが間違っているのでは？ g 括弧の位置が違うのでは？
2. を取得したら f を使用します。 curve を使用して、ルートが存在する適切な区間を調べます。次に uniroot .