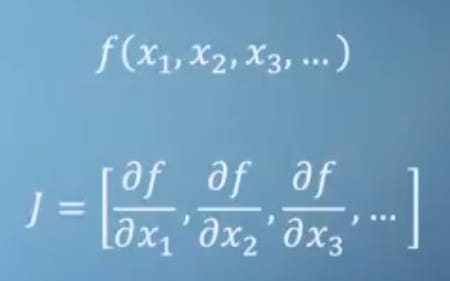[解決済み] Pytorch、グラディエント・アーキテクチャーとは？

質問

PyTorchのドキュメントを読んでいて、以下のような例を見つけました。

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)
print(x.grad)

ここで、x は初期変数で、そこから y が作られます（3-ベクトル）。問題は、勾配テンソルの0.1、1.0、0.0001の引数が何であるかということです。ドキュメントではあまり明確ではありません。

どのように解決するのですか？

PyTorchのサイトにはもう元のコードが見当たりません。

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)
print(x.grad)

上のコードの問題は、グラデーションの計算方法に基づいた関数が存在しないことです。つまり、パラメータ（関数が受け取る引数）の数やパラメータの次元がわからないのです。

これを完全に理解するために、私はオリジナルに近い例を作りました。

例1:

a = torch.tensor([1.0, 2.0, 3.0], requires_grad = True)
b = torch.tensor([3.0, 4.0, 5.0], requires_grad = True)
c = torch.tensor([6.0, 7.0, 8.0], requires_grad = True)

y=3*a + 2*b*b + torch.log(c)    
gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients,retain_graph=True)    

print(a.grad) # tensor([3.0000e-01, 3.0000e+00, 3.0000e-04])
print(b.grad) # tensor([1.2000e+00, 1.6000e+01, 2.0000e-03])
print(c.grad) # tensor([1.6667e-02, 1.4286e-01, 1.2500e-05])

私たちが想定している関数は y=3*a + 2*b*b + torch.log(c) であり、パラメータは内部に3つの要素を持つテンソルであると仮定します。

を考えることができる。 gradients = torch.FloatTensor([0.1, 1.0, 0.0001]) のように、これがアキュムレータであると考えることができます。

ご存知かもしれませんが、PyTorchのオートグラッドシステム計算はヤコビアン積と等価です。

一応、私たちのような関数がある場合は

y=3*a + 2*b*b + torch.log(c)

ヤコビアンは [3, 4*b, 1/c] . しかし、この ヤコビアン は、ある点での勾配を計算するために、PyTorchがどのように行っているかではありません。

PyTorchはフォワードパスと バックワードモード自動微分 (AD)を併用しています。

記号計算を伴わないので、数値による微分もありません。

数値微分とは、計算することである δy/δb に対して b=1 と b=1+ε ここで、εは小さい。

でグラデーションを使用しない場合は y.backward() :

例2

a = torch.tensor(0.1, requires_grad = True)
b = torch.tensor(1.0, requires_grad = True)
c = torch.tensor(0.1, requires_grad = True)
y=3*a + 2*b*b + torch.log(c)

y.backward()

print(a.grad) # tensor(3.)
print(b.grad) # tensor(4.)
print(c.grad) # tensor(10.)

をどのように設定したかに基づいて、あるポイントで結果を取得するだけです。 a , b , c のテンソルを初期化します。

をどのように初期化するかに注意してください。 a , b , c :

例3:

a = torch.empty(1, requires_grad = True, pin_memory=True)
b = torch.empty(1, requires_grad = True, pin_memory=True)
c = torch.empty(1, requires_grad = True, pin_memory=True)

y=3*a + 2*b*b + torch.log(c)

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(a.grad) # tensor([3.3003])
print(b.grad) # tensor([0.])
print(c.grad) # tensor([inf])

もし torch.empty() を使用し、かつ pin_memory=True を使用しない場合、異なる結果になることがあります。

また、グラデーションは累算器のようなものなので、必要なときはゼロにすることに注意してください。

例4:

a = torch.tensor(1.0, requires_grad = True)
b = torch.tensor(1.0, requires_grad = True)
c = torch.tensor(1.0, requires_grad = True)
y=3*a + 2*b*b + torch.log(c)

y.backward(retain_graph=True)
y.backward()

print(a.grad) # tensor(6.)
print(b.grad) # tensor(8.)
print(c.grad) # tensor(2.)

最後にPyTorchが使う用語のヒントをいくつか。

PyTorchは 動的な計算グラフ を作成します。これは木によく似ている。

ということで、よく耳にするのが 葉 という木があり、この木は 入力テンソル であり ルート は 出力テンソル .

勾配は、グラフを根から葉までたどり、途中のすべての勾配に 鎖の法則 . この掛け算はバックワードパスで行われます。

以前、私は PyTorch自動微分チュートリアル を作ったのですが、ADについての細かい説明があって面白かったので紹介します。