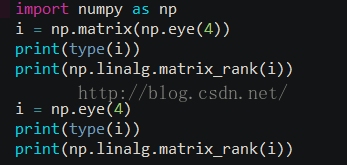
Python Numpyのarrayarrayとmatrixmatrix

プロヴァンス http://blog.chinaunix.net/uid-21633169-id-4408596.html

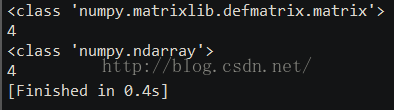
NumPyのメインオブジェクトは、同じ型の要素を持つ多次元配列である。これは、正の整数のタプルでインデックスされた、すべて1つの型の要素（通常、要素は数です）の表です。NumPyでは次元は軸と呼ばれ、軸の数はランクと呼ばれるが、線形代数でのランクと同じではなく、pythonでは numpy パッケージの linalg.matrix_rank メソッドは、次の例のように行列のランクを計算します。 <スパン ).

その結果、次のようになります。

線形代数におけるランクの定義：行列Aに0に等しくない次数rの部分式Dがあり、次数r+1のすべての部分式が（存在すれば）0に等しいとき、Dは行列Aの最高次の非ゼロの部分式と呼ばれ、数rは行列Aのランク（R（A）と表記）と呼ばれる。

numpyの配列と行列の違い。

matrixはarrayの分岐で、matrixもarrayも多くの場合で共通しており、どちらを使っても同じです。しかし現時点では、この2つが一般化できるのであればarrayを選択するのが公式のアドバイスです。arrayの方が柔軟で高速であり、多くの人が2次元のarrayをmatrixにも変換しているからです。
しかし、行列の利点は演算子表記が比較的簡単なことで、例えば2つの行列の掛け算は記号*を使いますが、配列の掛け算はそのように使うことができず、メソッド .dot() を使わなければなりません。
配列の利点は、2次元だけでなく、3次元、4次元、5次元...と表現できること、また、ほとんどのPythonプログラムで配列がより一般的に使用されていることです。

次に、numpyの多次元配列について説明します。

例えば、3次元空間の点の座標[1, 2, 3]は、軸が1つしかないのでランク1の配列になります。その軸の長さは3です。 別の例として、次の例では、配列のランクは2です（2次元を持つ）。1次元目の長さは2、2次元目の長さは3です。

[[ 1., 0., 0.],
 [ 0., 1., 2.]] 

NumPyの配列クラスは ndarray . よくアレイと呼ばれるものです。numpy.arrayは、1次元の配列しか扱えず、わずかな機能しか提供しないPythonの標準ライブラリクラスarray.arrayとは違うことに注意してください。より重要なndarrayオブジェクトのプロパティは以下の通りです。

• ndarray.ndim

  配列の軸の数。Pythonの世界では、軸の数はランクと呼ばれます。

• ndarray.shape

  配列の次元を表します。これは整数のタプルで，各次元における配列の大きさを表します．例えば、n 行 m 列の行列は (2,3) の shape 属性を持ち、このタプルの長さは明らかに rank、または dimension、または ndim 属性となります。

• ndarray.size

  配列の総要素数で、shapeプロパティのタプル要素の積に等しい。

• ndarray.dtype

  配列の要素の型を記述するために使用されるオブジェクトで、Pythonの標準的な型を使用してdtypeを作成または指定します。さらに、NumPy は独自のデータ型を提供します。

• ndarray.itemize

  配列の各要素のサイズをバイト数で指定します。例えば、float64型の要素の配列のitemiz属性は8（=64/8）、complex32型の要素の配列のitem属性は4（=32/8）です。

• ndarray.data

  実際の配列要素を含むバッファ。通常、配列の要素は常にインデックスで使用するため、このプロパティを使用する必要はありません。

例 1

>>> from numpy import *
>>> a = arange(15).reshape(3, 5)
>>> a
array([ 0, 1, 2, 3, 4],
       [ 5, 6, 7, 8, 9],
       [10, 11, 12, 13, 14]])
>>> a.shape
(3, 5)
>>> a.ndim
2
>>> a.dtype.name
'int32'
>>> a.itemsize
4
>>> a.size
15
>>> type(a)
numpy.ndarray
>>> b = array([6, 7, 8])
>>> b
array([6, 7, 8])
>>> type(b)
numpy.ndarray 

<スパン 配列の作成

配列を作成する方法はいくつかあります。

例えば、通常のPythonのリストやタプルから配列を作成するには、array関数を使用することができます。作成される配列の型は、元の配列の要素の型から導かれます。

>>> from numpy import *
>>> a = array( [2,3,4] )
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int32')
>>> b = array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64') 

よくある間違いは、1つの引数として値のリストを提供する代わりに、複数の数値引数で配列を呼び出すことです。

>>> a = array(1,2,3,4) # WRONG

>>> a = array([1,2,3,4]) # RIGHT 

配列は、配列を含む配列を2次元配列に、配列を含む配列を3次元配列に、といった具合に変換する。

>>> b = array( [ (1.5,2,3), (4,5,6) ] )
>>> b
array([ 1.5, 2. , 3. ],
       [ 4., 5., 6. ]]) 

を指定することで、作成時に配列の種類を表示することができます。

>>> c = array( [ [1,2], [3,4] ], dtype=complex )
>>> c
array([ 1.+0.j, 2.+0.j],
       [ 3.+0.j, 4.+0.j]]) 

通常、配列の要素は最初は不明ですが、そのサイズは既知です。そのため、NumPyではプレースホルダーを使って配列を作成する関数を多数用意しています。これにより、配列を展開する必要性と演算の高コストを最小限に抑えることができます。

関数 function はすべて 0 の配列を作成し、関数 ones はすべて 1 の配列を作成し、関数 empty は内容がランダムでメモリの状態に依存する配列を作成します。作成されるデフォルトの配列タイプ (dtype) はすべて float64 です。

>>> zeros( (3,4) )
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0., 0.]])
>>> ones( (2,3,4), dtype=int16 ) # dtype can also be specified
array([[ 1, 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1]],
       [[ 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1, 1]]], dtype=int16)
>>> empty( (2,3) )
array([[ 3.73603959e-262, 6.02658058e-154, 6.55490914e-260],
       [ 5.30498948e-313, 3.14673309e-307, 1.00000000e+000]]) 

シリーズを作るために、NumPy はリストの代わりに配列を返す配列のような関数を提供する。

>>> arange( 10, 30, 5 )
array([10, 15, 20, 25])
>>> arange( 0, 2, 0.3 ) # it accepts float arguments
array([ 0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8]) 

rangeが浮動小数点の引数を使用する場合、浮動小数点の精度に限界があるため、取得する要素数を予測できないことが多い。したがって、ステップサイズを指定するためにrangeを使うのではなく、linspace関数を使って欲しい要素数を受け取る方が良い。

その他の関数 array, zeros, zeros_like, ones, ones_like, empty, empty_like, arange, linspace, rand, randn, fromfunction, fromfile は、以下のものを参照しています。 NumPyの例

配列を表示する

配列を表示するとき、NumPyはネストされたリストのような形式で表示しますが、そのレイアウトは以下のとおりです。

• 最後の軸は左から右へ印刷されます
• 後続の軸は上から下へ印刷されます
• 残りの軸は上から下に向かって印刷され、各スライスは空白行で次のスライスと区切られる

1次元の配列は行として、2次元の数値は行列として、3次元の数値は行列リストとして出力されます。

>>> a = arange(6) # 1d array
>>> print a
[0 1 2 3 4 5]
>>>
>>> b = arange(12).reshape(4,3) # 2d array
>>> print b
[[ 0 1 2]
 [ 3 4 5]
 [ 6 7 8]
 [ 9 10 11]]
>>>
>>> c = arange(24).reshape(2,3,4) # 3d array
>>> print c
[[ 0 1 2 3
  [ 4 5 6 7]
  [ 8 9 10 11]]

 [[12 13 14 15]]
  [[16 17 18 19]]
  [[20 21 22 23]]] 

リシェイプの詳細については、シェイプ操作のセクションを参照してください。

配列が大きすぎて印刷できない場合、NumPy は自動的に中央部分を省略し、角だけを印刷します。

>>> print arange(10000)
[ 0 1 2 ... , 9997 9998 9999]
>>>
>>> print arange(10000).reshape(100,100)
[[ 0 1 2 ... , 97 98 99]
 [ 100 101 102 ... , 197 198 199]
 [ 200 201 202 ... , 297 298 299]
 ... ,
 [ 9700 9701 9702 ... , 9797 9798 9799]
 [9800 9801 9802 ... , 9897 9898 9899]
 [9900 9901 9902 ... , 9997 9998 9999]] 

NumPyのこの動作を無効にし、配列全体を強制的に印刷します。printoptionsパラメータを設定して、印刷オプションを変更することができます。

>>> set_printoptions(threshold='nan') 

<スパン 基本操作

配列の算術演算は要素ごとに行われます。新しい配列が作成され、結果が入力されます。

>>> a = array( [20,30,40,50] )
>>> b = arange( 4 )
>>> b
array([0, 1, 2, 3])
>>> c = a-b
>>> c
array([20, 29, 38, 47])
>>> b**2
array([0, 1, 4, 9])
>>> 10*sin(a)
array([ 9.12945251, -9.88031624, 7.4511316 , -2.62374854])
>>> a<35
array([True, True, False, False], dtype=bool) 

NumPyの乗算演算子*が要素ごとの計算を指示する多くの行列言語とは異なり、行列の乗算はdot関数や行列オブジェクトを作成することで実装できます（チュートリアルの行列の章を参照）。

>>> A = array( [[1,1],
...             [0,1]] )
>>> B = array( [[2,0],
...             [3,4]] )
>>> A*B # elementwise product
array([[2, 0],
       [0, 4]])
>>> dot(A,B) # matrix product
array([[5, 4],
       [3, 4]]) 

演算子の中には、+=や*=のように、新しい配列を作らずに既存の配列を変更するために使われるものもあります。

>>> a = ones((2,3), dtype=int)
>>> b = random.random((2,3))
>>> a *= 3
>>> a
array([[3, 3, 3],
       [3, 3, 3]])
>>> b += a
>>> b
array([[ 3.69092703, 3.8324276 , 3.0114541 ],
       [ 3.18679111, 3.3039349 , 3.37600289]])
>>> a += b # b is converted to integer type
>>> a
array([[6, 6, 6],
       [6, 6, 6]]) 

異なる型の配列に対して操作を行う場合、結果の配列はより一般的かつ正確に知ることができます（この動作をアップキャストと呼びます）。

>>> a = ones(3, dtype=int32)
>>> b = linspace(0,pi,3)
>>> b.dtype.name
'float64'
>>> c = a+b
>>> c
array([ 1. , 2.57079633, 4.14159265])
>>> c.dtype.name
'float64'
>>> d = exp(c*1j)
>>> d
array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
       -0.54030231-0.84147098j])
>>> d.dtype.name
'complex128' Many non-array operations, such as calculating the sum of all elements of an array, are implemented as methods of the ndarray class

>>> a = random.random((2,3))
>>> a
array([ 0.6903007 , 0.39168346, 0.16524769],
       [ 0.48819875, 0.77188505, 0.94792155]])
>>> a.sum()
3.4552372100521485
>>> a.min()
0.16524768654743593
>>> a.max()
0.9479215542670073 

これらの操作は、デフォルトでは配列の形状に関係なく、数値のリストであるかのように配列に適用されます。しかし、axisパラメータを指定することで、配列の指定された軸に操作を適用することができます。

>>> b = arange(12).reshape(3,4)
>>> b
array([ 0, 1, 2, 3],
       [ 4, 5, 6, 7],
       [ 8, 9, 10, 11]])
>>>
>>> b.sum(axis=0) # sum of each column
array([12, 15, 18, 21])
>>>
>>> b.min(axis=1) # min of each row
array([0, 4, 8])
>>>
>>> b.cumsum(axis=1) # cumulative sum along each row
array([ 0, 1, 3, 6],
       [ 4, 9, 15, 22],
       [ 8, 17, 27, 38]]) 

<スパン 汎用関数(ufunc)

NumPyには、sin, cos, expといった一般的な数学関数が用意されています。NumPyでは、これらはquot;generic functions" (ufunc)と呼ばれます。NumPyのこれらの関数は、配列の要素に対して操作を行い、出力として配列を生成します。

>>> B = arange(3)
>>> B
array([0, 1, 2])
>>> exp(B)
array([ 1. , 2.71828183, 7.3890561 ])
>>> sqrt(B)
array([ 0. , 1. , 1.41421356 ])
>>> C = array([2., -1., 4.])
>>> add(B, C)
array([ 2., 0., 6.]) 

<スパン その他の関数 all, alltrue, any, apply along axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, conjugate, corrcoef, cov, cross, cumprod, cumsum, diff, dot, floor, inner, inv, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, som true, sort, std, sum, trace, transpose, var, vdot, vectorize, where また，参照：index.index.index.index.index.index.index.index.index.index.index.index.com（英語）。 NumPyの例

<スパン インデックス、スライス、イテレーション

<スパン 一次元 と同じように、配列のインデックス付け、スライス、反復処理が可能です。 リスト や他のPythonのシーケンスと同じです。

>>> a = arange(10)**3
>>> a
array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729])
>>> a[2]
8
>>> a[2:5]
array([ 8, 27, 64])
>>> a[:6:2] = -1000 # equivalent to a[0:6:2] = -1000; from start to position 6, exclusive, set every 2nd element to -1000
>>> a
array([-1000, 1, -1000, 27, -1000, 125, 216, 343, 512, 729])
>>> a[ : :-1] # reversed a
array([ 729, 512, 343, 216, 125, -1000, 27, -1000, 1, -1000])
>>> for i in a:
...         print i**(1/3.),
...
nan 1.0 nan 3.0 nan 5.0 6.0 7.0 8.0 9.0 

<スパン 多次元 配列は1軸につき1つのインデックスを持つことができます。これらのインデックスはカンマで区切られたタプルによって与えられます。

>>> def f(x,y):
...         return 10*x+y
...
>>> b = fromfunction(f,(5,4),dtype=int)
>>> b
array([ 0, 1, 2, 3],
       [10, 11, 12, 13],
       [20, 21, 22, 23],
       [30, 31, 32, 33],
       [40, 41, 42, 43]])
>>> b[2,3]
23
>>> b[0:5, 1] # each row in the second column of b
array([ 1, 11, 21, 31, 41])
>>> b[ : ,1] # equivalent to the previous example
array([ 1, 11, 21, 31, 41])
>>> b[1:3, : ] # each column in the second and third row of b
array([[10, 11, 12, 13],
       [20, 21, 22, 23]]) 

軸の数より少ない軸が提供された場合、欠落したインデックスはスライス全体とみなされます。

>>> b[-1] # the last row. Equivalent to b[-1,:]
array([40, 41, 42, 43]) 

b[i]の括弧内の式はiとして扱い、残りの軸を表すために:を連ねる。.

ドット (...) は、完全なインデックス付きタプルを生成するために必要な多くのセミコロンを表します。xがランク5の配列（すなわち5つの軸を持つ）である場合，:

• x[1,2,...] は x[1,2,:,:,:] と等価である。
• x[...,3] は x[:,:,:,:,:,3] と等価である。
• x[4,...,5,:] は x[4,:,,5,:] と等価である。

 >>> c = array( [ [[ 0, 1, 2], # a 3D array (two stacked 2D arrays) ... [ 10, 12, 13]], ... ... [[100,101,102], ... [110,112,113]] ) >>> c.shape (2, 2, 3) >>> c[1,...] # same as c[1,:,:] or c[1] array([[100, 101, 102], [110, 112, 113]]) >>>> c[... ,2] # same as c[:,:,2] array([[ 2, 13], [102, 113]]) 

<スパン イテレーション 多次元配列は1軸目用。 2

>>> for row in b:
...         print row
...
[0 1 2 3]
[10 11 12 13]
[20 21 22 23]
[30 31 32 33]
[40 41 42 43] 

しかし、配列の各要素に対して操作を行いたい場合は、配列の要素に対するイテレータであるflat属性を使用することができます。

>>> for element in b.flat:
...         print element,
...
0 1 2 3 10 11 12 13 20 21 22 23 30 31 32 33 40 41 42 43 

<スパン その他の [], ..., 新軸, ndenumerate, インデックス, インデックス指数 リファレンス NumPyの例

<スパン 形状操作

配列の形状を変更する

配列の形状は、各軸の要素数によって決定されます。

>>> a = floor(10*random.random((3,4)))
>>> a
array([ 7., 5., 9., 3.],
       [ 7., 2., 7., 8.],
       [ 6., 8., 3., 2.]])
>>> a.shape
(3, 4) 

<スパン 配列の形状を複数のコマンドで変更することができます。

>>> a.ravel() # flatten the array
array([ 7., 5., 9., 3., 7., 2., 7., 8., 6., 8., 3., 2.])
>>> a.shape = (6, 2)
>>> a.transpose()
array([ 7., 9., 7., 7., 7., 6., 3.],
       [ 5., 3., 2., 8., 8., 2.]]) 

<スパン ravel() によって平坦化された配列の要素の順序は、通常 "C-style"、つまり、右端のインデックスが最も速く変化するので、要素 a[0,0] の次は a[0,1] です。NumPy は通常、この順序でデータを保持する配列を作成するので、ravel() は常にその引数をコピーする必要はありません。 3 . ただし、他の配列でスライスされていたり、変わったオプションがある場合は、コピーする必要がある場合があります。関数 reshape() と ravel() は、オプションの引数を持つ FORTRAN 形式の配列として構築することもできます。つまり、一番左のインデックスが最も速く変化します。

reshape関数は引数の形状を変更して返し、resize関数は配列そのものを変更する。

>>> a
array([ 7., 5.],
       [ 9., 3.],
       [ 7., 2.],
       [ 7., 8.],
       [ 6., 8.],
       [ 3., 2.]])
>>> a.resize((2,6))
>>> a
array([ 7., 5., 9., 3., 7., 2.],
       [ 7., 8., 6., 8., 3., 2.]]) 

形状変更操作で寸法が-1された場合、その寸法は自動的に計算される

<スパン その他のシェイプ、リシェイプ、リサイズ、ラベリングに関するリファレンス NumPyの例

<スパン 異なる配列を結合（スタック）する

異なる軸に沿ってアレイを積み重ねる方法がいくつかあります。

>>> a = floor(10*random.random((2,2)))
>>> a
array([ 1., 1.],
       [ 5., 8.]])
>>> b = floor(10*random.random((2,2)))
>>> b
array([ 3., 3.],
       [ 6., 0.]])
>>> vstack((a,b))
array([[ 1., 1.],
       [ 5., 8.],
       [ 3., 3.],
       [ 6., 0.]])
>>> hstack((a,b))
array([[ 1., 1., 3., 3,]
       [ 5., 8., 6., 0.]]) 

column_stack 関数は、一次元配列を列単位で二次元配列に合成するもので、一次元配列の vstack に相当する。

>>> column_stack((a,b)) # With 2D arrays
array([ 1., 1., 3., 3.],
       [ 5., 8., 6., 0.]])
>>> a=array([4.,2.])
>>> b=array([2.,8.])
>>> a[:,newaxis] # This allows to have a 2D columns vector
array([[4.],
       [ 2.]])
>>> column_stack((a[:,newaxis],b[:,newaxis]))
array([ 4., 2.],
       [ 2., 8.]])
>>> vstack((a[:,newaxis],b[:,newaxis])) # The behavior of vstack is different
array([[ 4.],
       [ 2.],
       [ 2.],
       [ 8.]]) 

一方、row_stack関数は、1次元配列を行のある2次元配列に結合するものである。

2次元以上の配列の場合、hstackは第2軸、vstackは第1軸に沿って結合し、concatenateは結合する軸をオプションの引数で指定できる。

<スパン 備考

複雑な場合、r_[]とc_[]は、ある方向に沿って結合した数を作るのに便利で、範囲表記（":"）が可能です。

>>> r_[1:4,0,4]
array([1, 2, 3, 0, 4]) 

<スパン 引数として配列を使用する場合、r_ と c_ のデフォルトの動作は vstack と hstack によく似ていますが、組み合わせを取る軸の指定を与えるオプション引数を許可します。

<スパン その他の関数 hstack , vstack , column_stack , row_stack , concatenate , c_ , r_ については、以下を参照してください。 NumPyの例 .

<スパン 配列を複数の小さな配列に分割する

hsplit では、配列をその横軸に沿って分割したり、同じ形の配列の数を指定して返したり、分割後の列を指定したりすることができます。

>>> a = floor(10*random.random((2,12)))
>>> a
array([ 8., 8., 3., 9., 0., 4., 3., 0., 0., 0., 6., 4., 4,
       [ 0., 3., 2., 9., 6., 0., 4., 5., 7., 5., 1., 4.]])
>>> hsplit(a,3) # Split a into 3
[array([[ 8., 8., 3., 9.]],
       [ 0., 3., 2., 9.]]), array([[ 0., 4., 3., 0.],
       [ 6., 0., 4., 5.]]), array([[ 0., 6., 4., 4,]
       [ 7., 5., 1., 4.]])]
>>> hsplit(a,(3,4)) # Split a after the third and the fourth column
[array([[ 8., 8., 3.],
       [ 0., 3., 2.]]), array([[ 9.],
       [ 9.]]), array([[ 0., 4., 3., 0., 0., 6., 4., 4,]
       [ 6., 0., 4., 5., 7., 5., 1., 4.]])] 

vsplit は縦軸方向に分割し、配列 split はどの軸方向に分割するかを指定します。

<スパン コピーして表示

配列の演算や操作を行う場合、そのデータは新しい配列にコピーされる場合とされない場合があります。これは、初心者がしばしば混乱する原因となっています。3つのケースがあります。

<スパン 全くコピーしない

単純代入では、配列オブジェクトやそのデータはコピーされません。

>>> a = arange(12)
>>> b = a # no new object is created
>>> b is a # a and b are two names for the same ndarray object
True
>>> b.shape = 3,4 # changes the shape of a
>>> a.shape
(3, 4) 

Pythonは不定形なオブジェクトを参照として渡す 4 ということで、関数呼び出しでは配列はコピーされません。

>>> def f(x):
...     print id(x)
...
>>> id(a) # id is a unique identifier of an object
148293216
>>> f(a)
148293216 

表示と浅いコピー

異なる配列オブジェクトが同じデータを共有する。ビューメソッドは、同じデータを指す新しい配列オブジェクトを作成します。

>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c.shape = 2,6 # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c[0,4] = 1234 # a's data changes
>>> a
array([[ 0, 1, 2, 3],
       [[1234, 5, 6, 7],
       [ 8, 9, 10, 11]]) 

スライスされた配列は、そのビューの一つを返します。

>>> s = a[ : , 1:3] # spaces added for clarity; could also be written "s = a[:,1:3]"
>>> s[:] = 10 # s[:] is a view of s. Note the difference between s=10 and s[:]=10
>>> a
array([[ 0, 10, 10, 3],
       [ 1234, 10, 10, 7],
       [ 8, 10, 10, 11]]) 

<スパン ディープコピー

配列とそのデータを正確にコピーする方法です。

>>> d = a.copy() # a new array object with new data is created
>>> d is a
False
>>> d.base is a # d doesn't share anything with a
False
>>> d[0,0] = 9999
>>> a
array([[ 0, 10, 10, 3],
       [1234, 10, 10, 7],
       [ 8, 10, 10, 11]]) 

<スパン 機能・メソッドの概要

これは、NumPyの関数とメソッドのソートされたリストです。名前は NumPyの例 で、これらの関数が実際に使われている様子を見ることができます。 5

配列の作成

arange, array, copy, e