質問

ノーキャリブレーションの手法で深度マップを取得しようとしています。 SIFTで対応点を見つけて、基本行列を得ることができるのですが cv2.findFundamentalMat . 次に、私は cv2.stereoRectifyUncalibrated を使用して、各画像のホモグラフィ行列を取得します。最後に cv2.warpPerspective を使用して、視差を補正して計算しますが、これでは良い深度マップが作成できません。値が非常に高いので、もしやこれは warpPerspective で取得したホモグラフィ行列から回転行列を計算しなければならないのか、それとも stereoRectifyUncalibrated .

で得られるホモグラフィ行列の場合、射影行列はよくわからない。 stereoRectifyUncalibrated を修正する。

コードの一部です。

#Obtainment of the correspondent point with SIFT
sift = cv2.SIFT()

###find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(dst1,None)
kp2, des2 = sift.detectAndCompute(dst2,None)

###FLANN parameters
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)

flann = cv2.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)

good = []
pts1 = []
pts2 = []

###ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):
    if m.distance < 0.8*n.distance:
        good.append(m)
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)
    
    
pts1 = np.array(pts1)
pts2 = np.array(pts2)

#Computation of the fundamental matrix
F,mask= cv2.findFundamentalMat(pts1,pts2,cv2.FM_LMEDS)


# Obtainment of the rectification matrix and use of the warpPerspective to transform them...
pts1 = pts1[:,:][mask.ravel()==1]
pts2 = pts2[:,:][mask.ravel()==1]

pts1 = np.int32(pts1)
pts2 = np.int32(pts2)

p1fNew = pts1.reshape((pts1.shape[0] * 2, 1))
p2fNew = pts2.reshape((pts2.shape[0] * 2, 1))
    
retBool ,rectmat1, rectmat2 = cv2.stereoRectifyUncalibrated(p1fNew,p2fNew,F,(2048,2048))

dst11 = cv2.warpPerspective(dst1,rectmat1,(2048,2048))
dst22 = cv2.warpPerspective(dst2,rectmat2,(2048,2048))

#calculation of the disparity
stereo = cv2.StereoBM(cv2.STEREO_BM_BASIC_PRESET,ndisparities=16*10, SADWindowSize=9)
disp = stereo.compute(dst22.astype(uint8), dst11.astype(uint8)).astype(np.float32)
plt.imshow(disp);plt.colorbar();plt.clim(0,400)#;plt.show()
plt.savefig("0gauche.png")

#plot depth by using disparity focal length `C1[0,0]` from stereo calibration and `T[0]` the distance between cameras

plt.imshow(C1[0,0]*T[0]/(disp),cmap='hot');plt.clim(-0,500);plt.colorbar();plt.show()

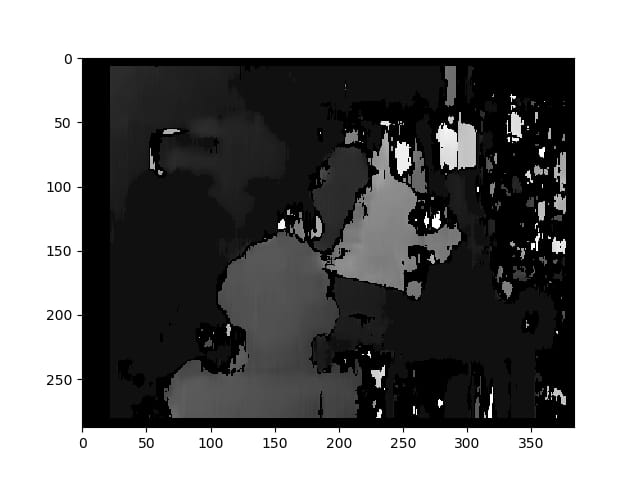
以下は、キャリブレーションを行わない方法で整流した写真です（と warpPerspective ):

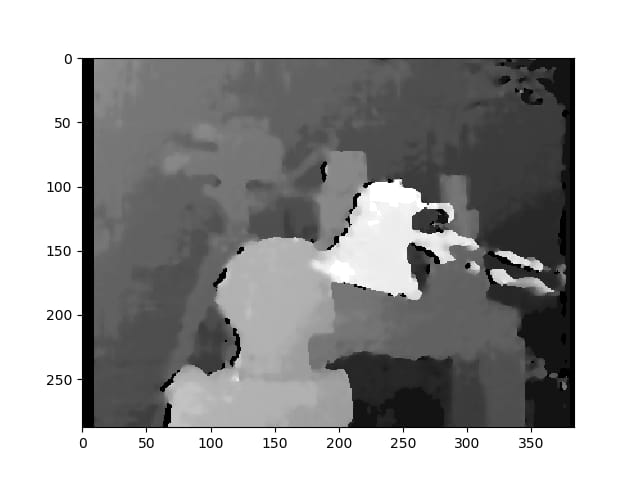
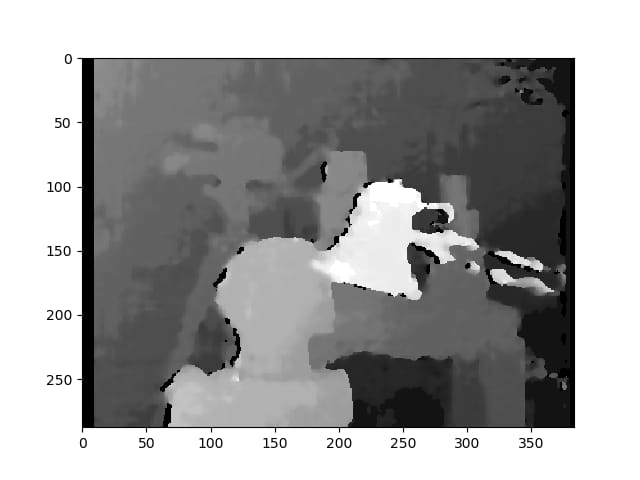
以下は、キャリブレート方式で整流した写真です。

2種類の写真で、どうしてこんなに差があるのかわからない。また、キャリブレーション方式では、位置が合っていないように見えます。

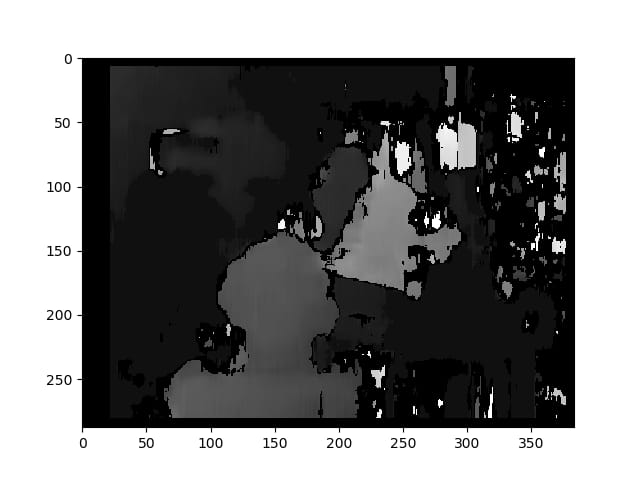
ノーキャリブレーション方式による視差マップ。

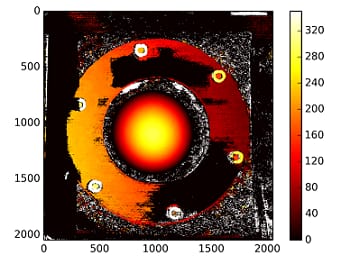
深さは.NETで計算されます。 C1[0,0]*T[0]/(disp) からのTで stereoCalibrate . 非常に高い値を示しています。

------------ 後で編集する ------------

再構成行列をマウントしようとしたのですが( [デヴァネ97]。 , [ガルシア01】。］ ) を "stereoRectifyUncalibrated" で得たホモグラフィ行列で表示していますが、結果はまだ良くありません。このやり方は正しいのでしょうか？

Y=np.arange(0,2048)
X=np.arange(0,2048)
(XX_field,YY_field)=np.meshgrid(X,Y)

#I mount the X, Y and disparity in a same 3D array 
stock = np.concatenate((np.expand_dims(XX_field,2),np.expand_dims(YY_field,2)),axis=2)
XY_disp = np.concatenate((stock,np.expand_dims(disp,2)),axis=2)

XY_disp_reshape = XY_disp.reshape(XY_disp.shape[0]*XY_disp.shape[1],3)

Ts = np.hstack((np.zeros((3,3)),T_0)) #i use only the translations obtained with the rectified calibration...Is it correct?


# I establish the projective matrix with the homography matrix
P11 = np.dot(rectmat1,C1)
P1 = np.vstack((np.hstack((P11,np.zeros((3,1)))),np.zeros((1,4))))
P1[3,3] = 1

# P1 = np.dot(C1,np.hstack((np.identity(3),np.zeros((3,1)))))

P22 = np.dot(np.dot(rectmat2,C2),Ts)
P2 = np.vstack((P22,np.zeros((1,4))))
P2[3,3] = 1

lambda_t = cv2.norm(P1[0,:].T)/cv2.norm(P2[0,:].T)


#I define the reconstruction matrix
Q = np.zeros((4,4))

Q[0,:] = P1[0,:].T
Q[1,:] = P1[1,:].T
Q[2,:] = lambda_t*P2[1,:].T - P1[1,:].T
Q[3,:] = P1[2,:].T

#I do the calculation to get my 3D coordinates
test = []
for i in range(0,XY_disp_reshape.shape[0]):
    a = np.dot(inv(Q),np.expand_dims(np.concatenate((XY_disp_reshape[i,:],np.ones((1))),axis=0),axis=1))
    test.append(a)

test = np.asarray(test)

XYZ = test[:,:,0].reshape(XY_disp.shape[0],XY_disp.shape[1],4)

解決方法は？

TLDR; より滑らかなエッジを持つ画像にはStereoSGBM (Semi Global Block Matching)を使用し、さらに滑らかにしたい場合はポストフィルタリングを使用します。

OPから元画像が提供されなかったので Tsukuba からの ミドルベリーのデータセット .

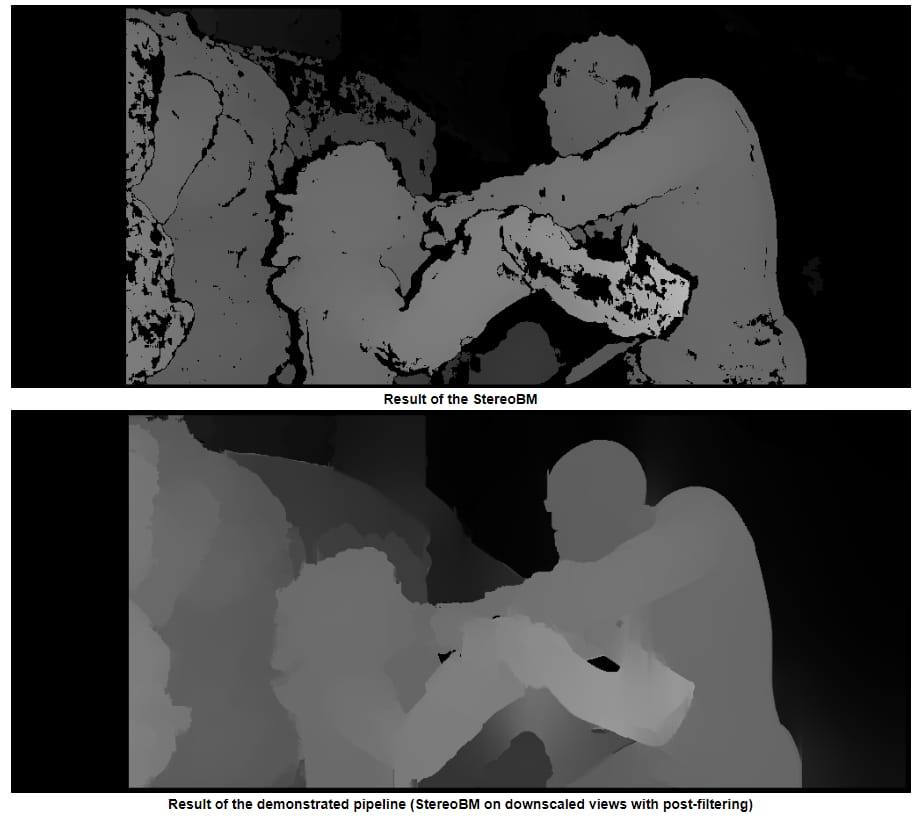
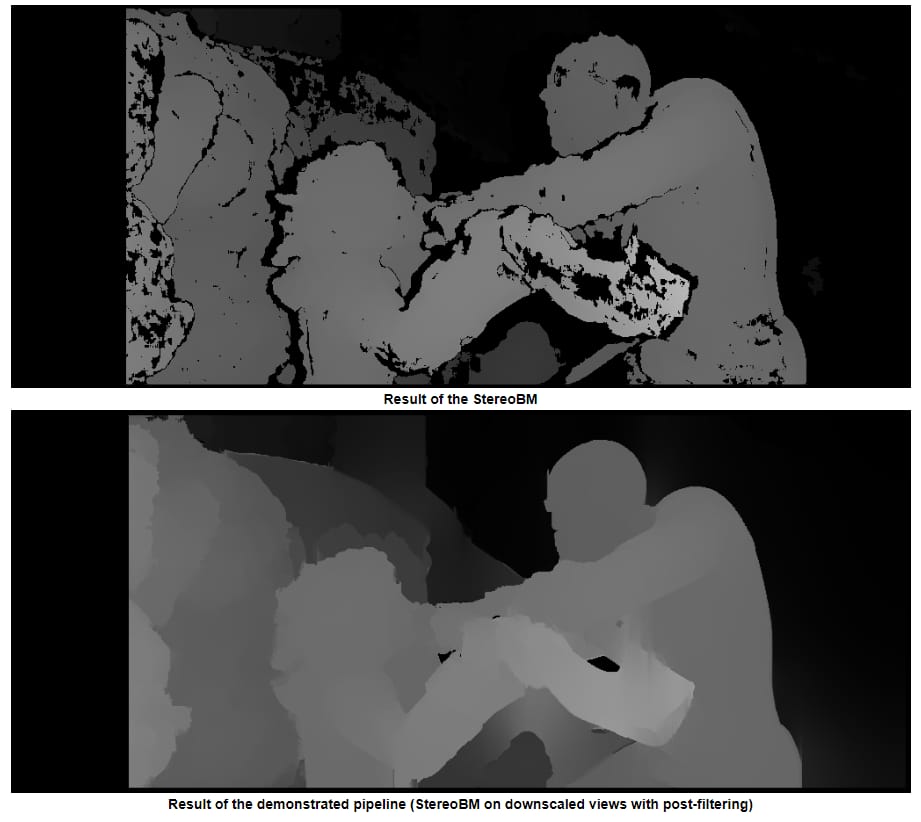
通常のStereoBMを使用した場合の結果

StereoSGBMを使用した結果（チューニング済み）

文献で見つけた最高の結果

出版物を見る こちら をご覧ください。

投稿フィルタリングの例（下記リンク参照）

理論編／OPの質問から考えるその他のこと

キャリブレーションされた平行化画像に大きな黒い部分があることから、これらの画像はキャリブレーションがあまりうまく行われていないのではないかと思われます。物理的なセットアップやキャリブレーション時の照明など、様々な理由が考えられますが、カメラキャリブレーションのチュートリアルはたくさんありますし、私の理解では、キャリブレーションされていないセットアップからより良い深度マップを得る方法を求めているのだと思います（これは100％明確ではありませんが、タイトルがこれをサポートしているようなので、人々はこれを見つけるためにここに来るのだと思います）。

基本的な考え方は正しいのですが、結果は間違いなく改善できます。この形式のデプスマッピングは、最高品質のマップを生成するものではありません（特に、キャリブレーションされていない場合）。最大の改善は、別のステレオマッチングアルゴリズムを使用することで得られると思われます。また、照明も大きな影響を及ぼしている可能性があります。右の画像は（少なくとも私の肉眼では）照明が弱く見えますが、これは再構成に干渉している可能性があります。まず、もう一方の画像と同じレベルまで明るくしてみるか、可能であれば新しい画像を収集 してみてください。ここから先は、あなたが元のカメラにアクセスできないと仮定して、新しい画像を集めたり、設定を変更したり、キャリブレーションを行うことは、範囲外であると考えます。(セットアップとカメラにアクセスできるのであれば、キャリブレーションを確認し、キャリブレーションされた方法を使用したほうがうまくいくと思います)。

使用したのは StereoBM は視差の計算（深度マップ）に使用され、それは機能しますが StereoSGBM の方がこの用途にははるかに適しています（より滑らかなエッジを処理できます）。その違いは以下の通りです。

この記事 は、その違いについてより深く解説しています。

ブロックマッチングは質感の高い画像（木の写真を想像してください）に焦点を当て、半グローバルブロックマッチングはサブピクセルレベルのマッチングと、より滑らかな質感の画像（廊下の写真を想像してください）に焦点を当てます。

カメラ固有の明示的なパラメータ、カメラの設定に関する詳細（焦点距離、カメラ間の距離、被写体までの距離など）、画像内の既知の寸法、または動き（たとえば、「Space」「Select」「Photo」「Motion」など）がない場合、このようなパラメータは使用されません。 構造から、モーション スケール感や回転は得られませんが、相対的な深度マップを生成することはできます。カメラのキャリブレーションを適切に行えば除去できるかもしれませんが、カメラがひどくない限り（レンズ系があまり歪んでいない）、キャリブレーションなしで妥当な結果を得ることができます。 標準的な構成 (基本的には、光軸ができるだけ平行に近く、視野が十分に重なるような向きにすることを意味します）。しかし、これはOPの問題ではないようで、彼はキャリブレーションされていない方法で正しく整流された画像を得ることに成功しました。

基本手順

1. 両方の画像から，少なくとも5つのよくマッチした点を見つけ，それを使って基本行列を計算します（好きな検出器とマッチャーを使うことができます．私は FLANN を使いましたが，SIFT が OpenCV 4.2.0 のメインバージョンにないので，検出は ORB で行いました）．
2. で基礎行列Fを計算する。 findFundamentalMat
3. で画像の歪みを解消 stereoRectifyUncalibrated と warpPerspective
4. で視差（深度マップ）を計算する。 StereoSGBM

結果はもっと良くなっています。

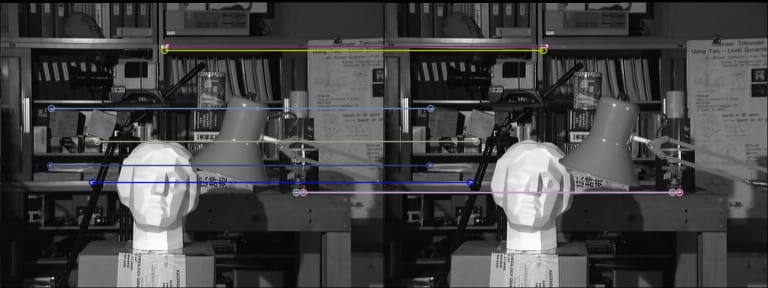
ORBとFLANNとのマッチング

歪みのない画像（左、右の順で表示）

格差

ステレオBM

この結果は、OPの問題（斑点、隙間、一部の領域での間違った深さ）に似ています。

StereoSGBM（チューニング済み）

この結果は、最終的な視差の計算を除けば、OPとほぼ同じ方法を用いており、OPの画像が提供されていれば、同様の改善が見られると思われます。

投稿フィルタリング

そこに この件に関する良い記事 OpenCVのドキュメントにあります。本当に滑らかなマップが必要な場合は、これを見ることをお勧めします。

上の写真の例は、シーンからフレーム1です ambush_2 の中で MPIシンテルデータセット .

フルコード (OpenCV 4.2.0 でテスト済み):

import cv2
import numpy as np
import matplotlib.pyplot as plt

imgL = cv2.imread("tsukuba_l.png", cv2.IMREAD_GRAYSCALE)  # left image
imgR = cv2.imread("tsukuba_r.png", cv2.IMREAD_GRAYSCALE)  # right image


def get_keypoints_and_descriptors(imgL, imgR):
    """Use ORB detector and FLANN matcher to get keypoints, descritpors,
    and corresponding matches that will be good for computing
    homography.
    """
    orb = cv2.ORB_create()
    kp1, des1 = orb.detectAndCompute(imgL, None)
    kp2, des2 = orb.detectAndCompute(imgR, None)

    ############## Using FLANN matcher ##############
    # Each keypoint of the first image is matched with a number of
    # keypoints from the second image. k=2 means keep the 2 best matches
    # for each keypoint (best matches = the ones with the smallest
    # distance measurement).
    FLANN_INDEX_LSH = 6
    index_params = dict(
        algorithm=FLANN_INDEX_LSH,
        table_number=6,  # 12
        key_size=12,  # 20
        multi_probe_level=1,
    )  # 2
    search_params = dict(checks=50)  # or pass empty dictionary
    flann = cv2.FlannBasedMatcher(index_params, search_params)
    flann_match_pairs = flann.knnMatch(des1, des2, k=2)
    return kp1, des1, kp2, des2, flann_match_pairs


def lowes_ratio_test(matches, ratio_threshold=0.6):
    """Filter matches using the Lowe's ratio test.

    The ratio test checks if matches are ambiguous and should be
    removed by checking that the two distances are sufficiently
    different. If they are not, then the match at that keypoint is
    ignored.

    https://stackoverflow.com/questions/51197091/how-does-the-lowes-ratio-test-work
    """
    filtered_matches = []
    for m, n in matches:
        if m.distance < ratio_threshold * n.distance:
            filtered_matches.append(m)
    return filtered_matches


def draw_matches(imgL, imgR, kp1, des1, kp2, des2, flann_match_pairs):
    """Draw the first 8 mathces between the left and right images."""
    # https://docs.opencv.org/4.2.0/d4/d5d/group__features2d__draw.html
    # https://docs.opencv.org/2.4/modules/features2d/doc/common_interfaces_of_descriptor_matchers.html
    img = cv2.drawMatches(
        imgL,
        kp1,
        imgR,
        kp2,
        flann_match_pairs[:8],
        None,
        flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS,
    )
    cv2.imshow("Matches", img)
    cv2.imwrite("ORB_FLANN_Matches.png", img)
    cv2.waitKey(0)


def compute_fundamental_matrix(matches, kp1, kp2, method=cv2.FM_RANSAC):
    """Use the set of good mathces to estimate the Fundamental Matrix.

    See  https://en.wikipedia.org/wiki/Eight-point_algorithm#The_normalized_eight-point_algorithm
    for more info.
    """
    pts1, pts2 = [], []
    fundamental_matrix, inliers = None, None
    for m in matches[:8]:
        pts1.append(kp1[m.queryIdx].pt)
        pts2.append(kp2[m.trainIdx].pt)
    if pts1 and pts2:
        # You can play with the Threshold and confidence values here
        # until you get something that gives you reasonable results. I
        # used the defaults
        fundamental_matrix, inliers = cv2.findFundamentalMat(
            np.float32(pts1),
            np.float32(pts2),
            method=method,
            # ransacReprojThreshold=3,
            # confidence=0.99,
        )
    return fundamental_matrix, inliers, pts1, pts2


############## Find good keypoints to use ##############
kp1, des1, kp2, des2, flann_match_pairs = get_keypoints_and_descriptors(imgL, imgR)
good_matches = lowes_ratio_test(flann_match_pairs, 0.2)
draw_matches(imgL, imgR, kp1, des1, kp2, des2, good_matches)


############## Compute Fundamental Matrix ##############
F, I, points1, points2 = compute_fundamental_matrix(good_matches, kp1, kp2)


############## Stereo rectify uncalibrated ##############
h1, w1 = imgL.shape
h2, w2 = imgR.shape
thresh = 0
_, H1, H2 = cv2.stereoRectifyUncalibrated(
    np.float32(points1), np.float32(points2), F, imgSize=(w1, h1), threshold=thresh,
)

############## Undistort (Rectify) ##############
imgL_undistorted = cv2.warpPerspective(imgL, H1, (w1, h1))
imgR_undistorted = cv2.warpPerspective(imgR, H2, (w2, h2))
cv2.imwrite("undistorted_L.png", imgL_undistorted)
cv2.imwrite("undistorted_R.png", imgR_undistorted)

############## Calculate Disparity (Depth Map) ##############

# Using StereoBM
stereo = cv2.StereoBM_create(numDisparities=16, blockSize=15)
disparity_BM = stereo.compute(imgL_undistorted, imgR_undistorted)
plt.imshow(disparity_BM, "gray")
plt.colorbar()
plt.show()

# Using StereoSGBM
# Set disparity parameters. Note: disparity range is tuned according to
#  specific parameters obtained through trial and error.
win_size = 2
min_disp = -4
max_disp = 9
num_disp = max_disp - min_disp  # Needs to be divisible by 16
stereo = cv2.StereoSGBM_create(
    minDisparity=min_disp,
    numDisparities=num_disp,
    blockSize=5,
    uniquenessRatio=5,
    speckleWindowSize=5,
    speckleRange=5,
    disp12MaxDiff=2,
    P1=8 * 3 * win_size ** 2,
    P2=32 * 3 * win_size ** 2,
)
disparity_SGBM = stereo.compute(imgL_undistorted, imgR_undistorted)
plt.imshow(disparity_SGBM, "gray")
plt.colorbar()
plt.show()