[解決済み】NumPyのeinsumを理解する。

質問

を正確に理解するのに苦労しています。 einsum は動作します。ドキュメントやいくつかの例を見ましたが、定着しないようです。

授業で習った例です。

C = np.einsum("ij,jk->ki", A, B)

を2つの配列のために使用します。 A と B .

これなら A^T * B しかし、よくわかりません（1つの転置をとっているのですよね）。どなたか、ここで起こっていることを正確に説明していただけませんか？ einsum )?

解決方法は？

(注：この回答は、短い ブログ記事 について einsum 少し前に書いたものです)

はどのようなものですか？ einsum を行うか？

2つの多次元配列があるとします。 A と B . では、仮に・・・。

• 掛ける A と B を特定の方法で実行して、新しい製品の配列を作成します。
• 合計 この新しい配列は、特定の軸に沿ったものです。
• 転置 新しい配列の軸を特定の順序で表示します。

という可能性が高いです。 einsum のようなNumPy関数の組み合わせよりも、より速く、よりメモリ効率的にこれを行うことができます。 multiply , sum と transpose が許可されます。

どのように einsum はどのように機能するのでしょうか？

ここで簡単な（しかし完全に些細なことではない）例を挙げます。次の2つの配列を例にとります。

A = np.array([0, 1, 2])

B = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])

を掛けることになります。 A と B を要素ごとに並べ、新しい配列の行にそって合計します。通常のNumPyでは、次のように記述します。

>>> (A[:, np.newaxis] * B).sum(axis=1)
array([ 0, 22, 76])

つまりここでは、インデックス作成操作で A 2つの配列の最初の軸を並べることで、乗算を放送することができます。そして、積の配列の行が合計されて答えが返されます。

ここで、もし einsum の代わりに、こう書くことができます。

>>> np.einsum('i,ij->i', A, B)
array([ 0, 22, 76])

は 署名 文字列 'i,ij->i' がここでのキーポイントで、少し説明が必要です。2つに分けて考えることができます。左側（の -> ) 2つの入力配列にラベルを付けました。の右側には -> そして、最終的に完成させたい配列にラベルを付けました。

以下は、その続きです。

• A は1つの軸を持っています。 i . そして B は2つの軸を持ち、軸0を i とし、軸1を j .

• By リピーター ラベル i を両方の入力配列に入力しています。 einsum この2つの軸は 乗算 を一緒にします。言い換えれば 配列を掛け合わせるのです A の各列と、配列 B と同じように A[:, np.newaxis] * B がそうである。

• に注目してください。 j はラベルとして出力されません。 i (最終的に1次元の配列にしたい). では 省略 というラベルを貼ることで einsum になります。 合計 をこの軸に沿わせています。つまり、商品の行を合計しているのです、まるで .sum(axis=1) が行います。

を使うために必要な知識は、基本的にこれだけです。 einsum . 少し遊んでみると、両方のラベルを出力に残しておくと便利です。 'i,ij->ij' と同じ）、製品の2次元配列が返されます。 A[:, np.newaxis] * B ). 出力ラベルなしとすると 'i,ij-> を実行すると、1つの数字が返されます。 (A[:, np.newaxis] * B).sum() ).

の素晴らしいところは einsum しかし、この方法では最初に商品の一時的な配列を作成することはなく、そのまま商品を合計していくだけです。これは、メモリの使用量を大幅に削減することにつながります。

少し大きな例

ドットプロダクトを説明するために、2つの新しい配列を紹介します。

A = array([[1, 1, 1],
           [2, 2, 2],
           [5, 5, 5]])

B = array([[0, 1, 0],
           [1, 1, 0],
           [1, 1, 1]])

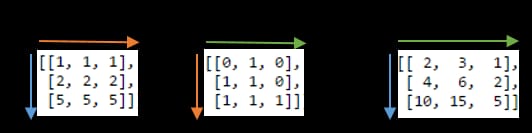
を使って内積を計算します。 np.einsum('ij,jk->ik', A, B) . のラベル付けを示す図です。 A と B と、この関数から得られる出力配列です。

そのラベルを見ると j の行が繰り返されています。 A の列と B . さらに、ラベル j は出力に含まれません - これらの製品を合計しているのです。ラベル i と k は出力用に保持されるので、2次元の配列が返されます。

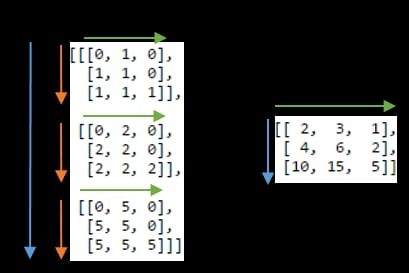
この結果を、ラベルが "H "の配列と比較すると、さらに分かりやすいかもしれません。 j は ない が合計されます。下の左側には、次のように記述した結果の3次元配列が表示されます。 np.einsum('ij,jk->ijk', A, B) (つまり、ラベルの j ):

和算軸 j は、右図のように期待通りの内積が得られます。

練習問題

をより実感していただくために einsum NumPyの配列操作でおなじみの、添え字記法を用いて実装すると便利です。軸の乗算と和算の組み合わせを含むものはすべて、以下のように書くことができます。 einsum .

AとBを同じ長さの2つの1次元配列とする。例えば A = np.arange(10) と B = np.arange(5, 15) .

• の合計が A は書くことができる。

  np.einsum('i->', A)
  
  

• 要素ごとの乗算。 A * B と書くことができる。

  np.einsum('i,i->i', A, B)
  
  

• 内積またはドットプロダクト。 np.inner(A, B) または np.dot(A, B) と書くことができる。

  np.einsum('i,i->', A, B) # or just use 'i,i'
  
  

• 外装品です。 np.outer(A, B) と書くことができる。

  np.einsum('i,j->ij', A, B)
  
  

2次元配列の場合。 C と D の場合、軸の長さは互換性がある（両方とも同じ長さ、または片方の長さが1）ので、以下にいくつかの例を示します。

• のトレースは C (主対角の和)。 np.trace(C) と書くことができる。

  np.einsum('ii', C)
  
  

• の要素ごとの乗算 C の転置と D , C * D.T と書くことができる。

  np.einsum('ij,ji->ij', C, D)
  
  

• の各要素に乗算します。 C という配列で D (4次元配列にするため)です。 C[:, :, None, None] * D と書くことができる。

  np.einsum('ij,kl->ijkl', C, D)