風力制御におけるKS原理を深く理解するためのpythonアルゴリズム

I. 事業背景

金融リスクコントロールの分野では、評価モデルの判別性を測るためにKS指標が用いられることが多く、リスクコントロールモデルの指標として最も求められているものの一つである。以下、判別概念、KS算出方法、経営指導の意味、幾何学的分析、数学的発想の観点から、KSを詳細に分析する。

II. 微分法の概念を直感的に理解する

データ探索において、独立変数xが従属変数yを判別しているかどうかを大まかに判断したい場合、サンプルをプラスとマイナスに分けて、変数の分布の違いを見ることが多いです。では、独立変数が有用であることをどのように判断するのでしょうか。直感的に理解すると、2つの分布の重なりが小さいほど、正のサンプルと負のサンプルの差が大きいことを表していれば、独立変数は正のサンプルと負のサンプルをより良く識別することができます。これを図1に示します。

例えるなら、この変数は、この分布を左右に引き離す一対の手であると想像してください。この手が強力であればあるほど、2つの確率分布は離れ、この変数がより分化していることを示している。

図1 - 正負のサンプル分布の違いの比較

Since the browser must execute the event handler before it knows if preventDefault() has been used, this results in a slight delay in the browser's response to scrolling.

So to make page scrolling silky smooth, starting with chrome56, the touchstart and touchmove event handlers registered on window, document, and body will default to passive: true. browsers ignore preventDefault() to scroll first. The browser ignores preventDefault() to scroll first.

Example.
wnidow.addEventListener('touchmove', func) has the same effect as the following sentence
wnidow.addEventListener('touchmove', func, { passive: true })

III. KS統計量の定義

KS (Kolmogorov-Smirnov) 統計は、A.N. Kolmogorov と N.V. Smirnov というソ連の二人の科学者によって提案されました。

リスクコントロールでは、KSは通常モデルの識別性を評価するために使用され、識別性が高いほどモデルのリスクランキング能力が高いことを意味する。

KSは、Emporical Cumulative Distribution Function (ecdf) に基づいています。

IV. KSの計算過程と業務分析

KSのよく使われる計算方法

step1: 等周波数、等尺性、カスタム距離のいずれかの変数をビンニングする。

step2: 各ビニング区間について、良いサンプルと悪いサンプルの数（goods）を計算する。

step3: 各ビン区間について、総良顧客に対する累積良顧客率（cum_good_rate）と総悪顧客に対する累積悪顧客率（cum_bad_rate）を計算する。

step4: 各サブボックス区間について、累積優良顧客に対する累積不良顧客の比率の絶対値を計算し、KS曲線を求める、である。

step5: これらの絶対値のうち最大値をとり、この変数の最終的なKS値を得る。

わかりやすくするために、上記のプロセスを具体的なデータで示す。

表1 KS算出工程表

上付きインジケーターの計算ロジック。

を取得することができます。

1. モデルスコアが高いほど延滞率が低くなるので、スコアの低いbad_rateはスコアの高いものに比べて相対的に高くなり、cum_bad_rate曲線はcum_good_rateよりも速い速度で成長する。cum_bad_rate曲線はcum_good_rate曲線よりも上にある。

2. 2. 各ビンのサンプル数は基本的に同じであり、周波数が等しいビンを示しています。

3. カットオフを0.65に制限した場合、そのcum_bad_rateは82.75%で、悪い顧客の82.75%が拒否されることを示すが、同時にcum_good_rateは29.69%で、良い顧客の29.69%が同時に拒否されることを示す。

4. bad_rateの傾向から、モデルはうまくソートされている。Aカードの場合、リスクレベルに応じてユーザーリスクを値付けする必要があるため、ソート性の要件は高くなると思われる。

5. モデルのKSは53.1%に達し、強い差別化ができており、これは理想的な状態である。実際の業務アプリケーションでは、合格率とbad_rateの関係をあらかじめ設定した条件に従って重み付けする必要があり、一般にカットオフは理想値で選ばれないので、KSは微分法の上限値であることがわかる。

6. Aカードの場合、通常KS52%に達することは難しいので、上の表のデータがAカードの結果であれば、モデルがオーバーフィットしていないかさらに確認する必要があります。

さらに注意しなければならないのは、KSは貸出サンプルで評価され、貸出サンプルは常にフルサンプルに対してバイアスがかかるということです。裸の風力制御システムの場合、バイアスは小さくなり、逆に風力制御システムがより良い仕事をすれば、バイアスは大きくなります。つまり、KSは単なる数字ではなく、その背景には多くの理由があり、ビジネスの文脈で具体的に分析する必要があるのです。

KSが悪い場合、以下のようなチェックを行うことで、目的を達成することができます。

1. 入力される変数が戦略によって使用されていることを確認する。重複した変数を使用すると、ヒットすべき不良顧客にヒットしないことがあり、モデルの効果が低下する。

2. 学習用サンプルと検証用サンプルの間に、時間的分布、特定の特徴の分布、特別な特徴のヒットなど、客層に大きな違いがあるかどうかをチェックする。

3. 税務シナリオなど、対象シナリオに特化した新しい特徴を開発し、特徴導出を行う際に税務指標をより重視する。例えば、長期リスクの特定には強い財務属性変数を使用し、不正リスクにはいくつかの短期的な負の変数を使用するなどである。

4.サブグループモデリングだが、オーバーフィッティングを防ぐため、安定性と変動性を条件とする。

5. 個性で共通性を押し通そうとする、悪しき顧客分析。

表1のデータを可視化すると、主に最後の3列のデータ、すなわちcum_good_rate、cum_bad_rate、KSを用いて、以下のコードと画像でKS曲線が得られます。

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
cum_good_rate = np.array([0.00,0.05,0.12,0.20,0.30,0.41,0.53,0.71,0.86,1.00])
cum_bad_rate = np.array([0.26,0.45,0.59,0.72,0.83,0.90,0.97,0.99,1.00,1.00])
x = np.linspace(0, 1, 10)
plt.plot(x, cum_good_rate, label = 'cum_good_rate')
plt.plot(x, cum_bad_rate, label = 'cum_bad_rate')
plt.plot(x, cum_bad_rate - cum_good_rate, label = 'KS')
plt.title('KS Curve', fontsize = 16)
plt.grid(True,linestyle = ':', color = 'r', alpha = 0.7)
plt.axhline(y = 0.53, c = 'r', ls = '--', lw = 3) # Draw a horizontal reference line parallel to the x-axis
plt.axvline(x = 0.43, c = 'r', ls = '--', lw = 3) #plot a vertical reference line parallel to the y-axis
plt.legend()
plt.show()

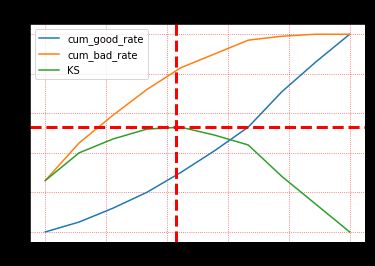
図2 KSカーブ

ここまでで、KS算出の基本プロセス、評価基準、経営指導の意味合い、最適化の考え方は理解できたので、次にいくつかの質問をします。

1. リスクコントロールにおいて、精度や再現性などではなく、モデルの有効性を評価するためにKSがよく使われるのはなぜか？

2. max KSはあくまでマクロの結果であり、異なるカットオフ値でmaxにした場合のモデル効果の違いは何でしょうか？

3. 一般的にKSは大きければ大きいほど良いとされていますが、通常75％以上のKSは信頼性が低いとされているのはなぜですか？

V. リスクコントロールでKSを選択する理由

風管理モデリングでは、サンプルラベルをGBIXの4つに分けることが多く、G=Good（良い人、0と表記）、B=Bad（悪い人、1と表記）、I=Indeterminate（不定、実績期間外）、X=Exclusion（除外、異常サンプル）の4つに分けています。

ここで重要なのは、GoodとBadの間の定義は、実際のビジネス要件によって曖昧で連続的であることが多いということである。以下、理解を助けるために2つの例を挙げる。

例1：漠然としている

12期間のクレジット商品において、パフォーマンス期間を最初の6期間に設定した場合、S6D15（最初の6期間のうち、15日以上延滞した期間）は1、それ以外は0となる。しかしその後、履行期間を3期間に調整すると、**"最初の3期間は正常に支払われるが、4~6期間だけが15日を超えて延滞している"**この部分のサンプルでは、当初定義したラベルが1から0に変わる。したがってビジネスニーズが異なり、ラベルの定義が絶対的でない結果となる。 したがって、良いサンプルと悪いサンプルの定義は、実際のビジネスニーズに基づき、頭でっかちではなく、ビジネスを十分に理解し分析した上で決定する必要があります。

例2：コンティニュイティ

しかし、29日経過したユーザーと31日経過したユーザーの間には、実際にはハード的に交差しない区間があり、29日経過したユーザーはさらに悪化して31日経過する可能性があります。

期限切れ深刻度の定義は本来、やや主観的なものなので、期限切れ日数の数日の差がどの程度本質的な差になるかはわからないので、分類問題に置き換える目的で1と0の境界のハードな定義をやっても、ビジネス上の理解は連続した問題であることに変わりはないのです。

したがって、リスクコントロールにおいて、yは白か黒か（離散）で定義されるのではなく、おそらく確率分布（連続）で測られるのがより合理的です。

では、なぜ確率の観点から正と負のサンプルの差を測る傾向にあるKSという指標を選んだかというと、まさに正と負のサンプルの間に曖昧さと連続性があるからで、KSも連続曲線になるのです。しかし、最終的に最大値をとるのは、KS曲線の大きな特徴を抽出して、互いに比較しやすいようにするのが主な理由です。

以上、風力制御におけるKSの原理を理解するためのpythonアルゴリズムの詳細を紹介しました。