[解決済み] すべての島をつなぐために必要な最低限のコストは？

質問

大きさ N×M . いくつかのセルは 島 で示され、他のセルは 水 . 各水マスには、そのマスに橋をかけたときのコストを表す数字が書かれています。あなたは、すべての島が接続できる最小のコストを見つけなければならない。あるセルと他のセルが辺または頂点を共有している場合、そのセルは接続されています。

この問題を解くために、どのようなアルゴリズムが使えるか？N、Mの値が非常に小さい場合、例えばNxM <= 100の場合、ブルートフォースアプローチとして何が使えるか？

例 : 与えられた画像において、緑色のセルは島、青色のセルは水、水色のセルは橋をかけるべきセルを示している。したがって、次の画像に対する答えは次のようになる。 17 .

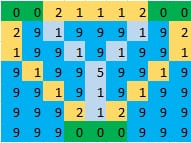
当初は、すべての島をノードとし、すべての島のペアを最短距離の橋で結ぶことを考えました。しかし、この方法では、エッジが重なり合っている場合を見逃してしまいます。 例えば の場合、任意の2つの島々の最短距離は 7 (黄色で表示)であるから、最小スパニングツリーを用いると、その答えは 14 となりますが、本来は 11 (水色でマーク)でなければなりません。

どのように解決するのですか？

この問題にアプローチするために、私は整数計画法の枠組みを使い、3組の決定変数を定義します。

• x_ij : 水域の位置(i, j)に橋を架けるかどうかの2値指標変数。
• y_ijbcn : 水域(i, j)が島bと島cを結ぶn^番目の地点であるかどうかの二値指標である。
• l_bc : 島bと島cが直接つながっているかどうか（bからcへの橋のマス目だけを歩けるかどうか）の2値指標変数。

橋の建設コストについて c_ij とすると、最小化すべき目的値は sum_ij c_ij * x_ij . このモデルに以下の制約を追加する必要がある．

• 私たちは y_ijbcn 変数が有効であることを確認する必要があります。水の広場には常に橋をかけないと行けないので y_ijbcn <= x_ij はすべての水の場所(i, j)に対して成り立つ。さらに y_ijbc1 は(i, j)が島bに接していなければ0でなければならない。最後に、n > 1について y_ijbcn は、ステップn-1で隣接する水の位置が使用された場合のみ使用できる。定義 N(i, j) を(i, j)に隣接する水のマスであると定義すると、これは次のようになる。 y_ijbcn <= sum_{(l, m) in N(i, j)} y_lmbc(n-1) .
• を確保する必要があります。 l_bc 変数が設定されるのは、b と c がリンクされている場合のみであることを確認する必要があります。もし私たちが I(c) を島cに接する場所と定義すると、これは l_bc <= sum_{(i, j) in I(c), n} y_ijbcn .
• 我々は、すべての島が直接または間接的にリンクされていることを保証する必要があります。これは次の方法で達成できます。島の空でない適切な部分集合Sごとに、S内の少なくとも1つの島がSの補集合（ここではS'と呼ぶ）内の少なくとも1つの島にリンクされていることを要求します。制約では、サイズ <= K/2（Kは島の数）の空でない集合Sごとに制約を追加することでこれを実装できます。 sum_{b in S} sum_{c in S'} l_bc >= 1 .

K個の島、W個の水広場、指定された最大経路長Nを持つ問題インスタンスに対して、次のような混合整数計画モデルである。 O(K^2WN) 変数と O(K^2WN + 2^K) の制約に従います。もちろん、問題のサイズが大きくなれば難解になりますが、気になるサイズであれば解けるかもしれません。スケーラビリティを実感するために、pulpパッケージを使ってpythonで実装してみます。まず、問題の下に3つの島がある7×9の小さい地図から始めてみましょう。

import itertools
import pulp
water = {(0, 2): 2.0, (0, 3): 1.0, (0, 4): 1.0, (0, 5): 1.0, (0, 6): 2.0,
         (1, 0): 2.0, (1, 1): 9.0, (1, 2): 1.0, (1, 3): 9.0, (1, 4): 9.0,
         (1, 5): 9.0, (1, 6): 1.0, (1, 7): 9.0, (1, 8): 2.0,
         (2, 0): 1.0, (2, 1): 9.0, (2, 2): 9.0, (2, 3): 1.0, (2, 4): 9.0,
         (2, 5): 1.0, (2, 6): 9.0, (2, 7): 9.0, (2, 8): 1.0,
         (3, 0): 9.0, (3, 1): 1.0, (3, 2): 9.0, (3, 3): 9.0, (3, 4): 5.0,
         (3, 5): 9.0, (3, 6): 9.0, (3, 7): 1.0, (3, 8): 9.0,
         (4, 0): 9.0, (4, 1): 9.0, (4, 2): 1.0, (4, 3): 9.0, (4, 4): 1.0,
         (4, 5): 9.0, (4, 6): 1.0, (4, 7): 9.0, (4, 8): 9.0,
         (5, 0): 9.0, (5, 1): 9.0, (5, 2): 9.0, (5, 3): 2.0, (5, 4): 1.0,
         (5, 5): 2.0, (5, 6): 9.0, (5, 7): 9.0, (5, 8): 9.0,
         (6, 0): 9.0, (6, 1): 9.0, (6, 2): 9.0, (6, 6): 9.0, (6, 7): 9.0,
         (6, 8): 9.0}
islands = {0: [(0, 0), (0, 1)], 1: [(0, 7), (0, 8)], 2: [(6, 3), (6, 4), (6, 5)]}
N = 6

# Island borders
iborders = {}
for k in islands:
    iborders[k] = {}
    for i, j in islands[k]:
        for dx in [-1, 0, 1]:
            for dy in [-1, 0, 1]:
                if (i+dx, j+dy) in water:
                    iborders[k][(i+dx, j+dy)] = True

# Create models with specified variables
x = pulp.LpVariable.dicts("x", water.keys(), lowBound=0, upBound=1, cat=pulp.LpInteger)
pairs = [(b, c) for b in islands for c in islands if b < c]
yvals = []
for i, j in water:
    for b, c in pairs:
        for n in range(N):
            yvals.append((i, j, b, c, n))

y = pulp.LpVariable.dicts("y", yvals, lowBound=0, upBound=1)
l = pulp.LpVariable.dicts("l", pairs, lowBound=0, upBound=1)
mod = pulp.LpProblem("Islands", pulp.LpMinimize)

# Objective
mod += sum([water[k] * x[k] for k in water])

# Valid y
for k in yvals:
    i, j, b, c, n = k
    mod += y[k] <= x[(i, j)]
    if n == 0 and not (i, j) in iborders[b]:
        mod += y[k] == 0
    elif n > 0:
        mod += y[k] <= sum([y[(i+dx, j+dy, b, c, n-1)] for dx in [-1, 0, 1] for dy in [-1, 0, 1] if (i+dx, j+dy) in water])

# Valid l
for b, c in pairs:
    mod += l[(b, c)] <= sum([y[(i, j, B, C, n)] for i, j, B, C, n in yvals if (i, j) in iborders[c] and B==b and C==c])

# All islands connected (directly or indirectly)
ikeys = islands.keys()
for size in range(1, len(ikeys)/2+1):
    for S in itertools.combinations(ikeys, size):
        thisSubset = {m: True for m in S}
        Sprime = [m for m in ikeys if not m in thisSubset]
        mod += sum([l[(min(b, c), max(b, c))] for b in S for c in Sprime]) >= 1

# Solve and output
mod.solve()
for row in range(min([m[0] for m in water]), max([m[0] for m in water])+1):
    for col in range(min([m[1] for m in water]), max([m[1] for m in water])+1):
        if (row, col) in water:
            if x[(row, col)].value() > 0.999:
                print "B",
            else:
                print "-",
        else:
            print "I",
    print ""

pulpパッケージのデフォルトソルバ（CBCソルバ）を使って実行すると1.4秒かかり、正しい解が出力されます。

I I - - - - - I I 
- - B - - - B - - 
- - - B - B - - - 
- - - - B - - - - 
- - - - B - - - - 
- - - - B - - - - 
- - - I I I - - - 

次に、問題の一番上にある、13×14のグリッドに7つの島がある完全な問題を考えてみましょう。

water = {(i, j): 1.0 for i in range(13) for j in range(14)}
islands = {0: [(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)],
           1: [(9, 0), (9, 1), (10, 0), (10, 1), (10, 2), (11, 0), (11, 1),
               (11, 2), (12, 0)],
           2: [(0, 7), (0, 8), (1, 7), (1, 8), (2, 7)],
           3: [(7, 7), (8, 6), (8, 7), (8, 8), (9, 7)],
           4: [(0, 11), (0, 12), (0, 13), (1, 12)],
           5: [(4, 10), (4, 11), (5, 10), (5, 11)],
           6: [(11, 8), (11, 9), (11, 13), (12, 8), (12, 9), (12, 10), (12, 11),
               (12, 12), (12, 13)]}
for k in islands:
    for i, j in islands[k]:
        del water[(i, j)]

for i, j in [(10, 7), (10, 8), (10, 9), (10, 10), (10, 11), (10, 12),
             (11, 7), (12, 7)]:
    water[(i, j)] = 20.0

N = 7

MIPソルバーはしばしば比較的早く良い解を得、その後その解の最適性を証明するために膨大な時間を費やします。上記と同じソルバー・コードを使用しても、プログラムは30分以内に完了しません。しかし、ソルバーにタイムアウトを与えることで、近似解を得ることができます。

mod.solve(pulp.solvers.PULP_CBC_CMD(maxSeconds=120))

この結果、目的値17の解が得られます。

I I - - - - - I I - - I I I 
I I - - - - - I I - - - I - 
I I - - - - - I - B - B - - 
- - B - - - B - - - B - - - 
- - - B - B - - - - I I - - 
- - - - B - - - - - I I - - 
- - - - - B - - - - - B - - 
- - - - - B - I - - - - B - 
- - - - B - I I I - - B - - 
I I - B - - - I - - - - B - 
I I I - - - - - - - - - - B 
I I I - - - - - I I - - - I 
I - - - - - - - I I I I I I 

得られた解の質を向上させるために、商用のMIPソルバー（学術機関であれば無料ですが、そうでない場合は無料ではない可能性があります）を使用することができます。たとえば、Gurobi 6.0.4のパフォーマンスです。やはり2分の時間制限があります（ただし、解答ログから、ソルバーは現在の最適解を7秒以内に見つけたと読み取れます）。

mod.solve(pulp.solvers.GUROBI(timeLimit=120))

これは実際に目的値16の解を見つけ、OPが手作業で見つけたものより良いものです!

I I - - - - - I I - - I I I 
I I - - - - - I I - - - I - 
I I - - - - - I - B - B - - 
- - B - - - - - - - B - - - 
- - - B - - - - - - I I - - 
- - - - B - - - - - I I - - 
- - - - - B - - B B - - - - 
- - - - - B - I - - B - - - 
- - - - B - I I I - - B - - 
I I - B - - - I - - - - B - 
I I I - - - - - - - - - - B 
I I I - - - - - I I - - - I 
I - - - - - - - I I I I I I