[解決済み] Dijkstraのアルゴリズムによる負の重み付け

質問

Dijkstraのアルゴリズムが負の重みで動作しない理由を理解しようとしています。上の例を読むと 最短経路 の例を読んで、私は次のシナリオを理解しようとしています。

    2
A-------B
 \     /
3 \   / -2
   \ /
    C

ホームページから

辺がすべて左から右へ向けられていると仮定すると Aから始めると、Dijkstraのアルゴリズムは、最小のエッジ(A,x)を選択することになります。 d(A,A)+length(edge)、すなわち(A,B)を選択する。次に、d(A,B)=2に設定し、次のように選択する。 d(A,y)+d(y,C) を最小化する別の辺 (y,C) を選択する． であり，d(A,C)=3 とする．しかし、AからBへの最短経路を見つけることはできない。 B、C を経由して、全長 1 の最短経路を見つけることはできません。

以下のDijkstraの実装を使うと、d[B]はなぜ更新されないのか理解できません。 1 (アルゴリズムが頂点Cに到達したとき、それはB上でrelaxを実行し、d[B]がに等しいことを確認します。 2 に等しいことを確認し、したがって、その値を 1 ).

Dijkstra(G, w, s)  {
   Initialize-Single-Source(G, s)
   S ← Ø
   Q ← V[G]//priority queue by d[v]
   while Q ≠ Ø do
      u ← Extract-Min(Q)
      S ← S U {u}
      for each vertex v in Adj[u] do
         Relax(u, v)
}

Initialize-Single-Source(G, s) {
   for each vertex v  V(G)
      d[v] ← ∞
      π[v] ← NIL
   d[s] ← 0
}

Relax(u, v) {
   //update only if we found a strictly shortest path
   if d[v] > d[u] + w(u,v) 
      d[v] ← d[u] + w(u,v)
      π[v] ← u
      Update(Q, v)
}

ありがとうございます。

ミール

どのように解決するのですか？

あなたが提案したアルゴリズムは、確かにこのグラフの最短経路を見つけることができますが、一般的にすべてのグラフを見つけることはできません。例えば、このようなグラフを考えてみましょう。

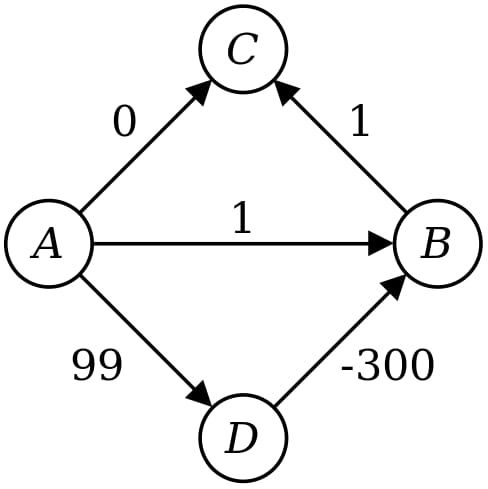
あなたのアルゴリズムの実行をトレースしてみましょう。

1. まず、d( A ) を 0 に、その他の距離を ∞ に設定します。
2. 次に、ノードを展開し A を設定し、d( B ) を 1 に、d( C )を0に、そしてd( D ) を 99 に設定します。
3. 次に、展開した C を、正味の変更なしに展開します。
4. 次に B を展開しますが、これは何の効果もありません。
5. 最後に D を展開し、d( B ) を -201 に変更します。

この最後に、しかし、そのd( C への最短経路はまだ0であることに注意してください。 C への最短パスは長さ -200 であるにもかかわらず、0 のままです。これは、あなたのアルゴリズムがすべてのノードへの正しい距離を計算していないことを意味する。さらに、各ノードから開始ノードへの行き方を示すバックポインタを保存していたとしても A から間違った経路で戻ってくることになる。 C から A .

この理由は、Dijkstraのアルゴリズム（とあなたのアルゴリズム）は 貪欲なアルゴリズム は、一度あるノードまでの距離を計算したら、見つかった距離は最適な距離でなければならないと仮定しています。言い換えれば、アルゴリズムは、拡張したノードの距離を取り、その距離が何であるかを変更することを自分自身に許さないのです。負のエッジの場合、あなたのアルゴリズム、およびダイクストラのアルゴリズムは、出発ノードから他のノードへの最適なパスのコストを実際に減少させる負のコストのエッジを見ることによって、"surprise"することができます。

これが役に立つことを願っています。