[解決済み】｜｜と！｜｜の演算子で、あらゆる論理式が可能か？

質問

論理式 ( a && b ) (両方とも a と b はブーリアン値を持つ) は次のように書くことができます。 !(!a || !b) , 例えば これは、次のような意味ではないでしょうか？ && は、"noneccesary"ですか？これは すべて を使用してのみ論理式を作成することができます。 || と ! ?

解決方法は？

はい、他の回答でも指摘されているように || と ! は 機能的に完全 . それを証明するために、論理変数間の16個の論理接続詞をすべて表現する方法を紹介します。 A と B :

• 真 : A || !A
• A NAND B : !A || !B
• BはAを意味する : !B || A
• AはBを意味する : !A || B
• A OR B : A || B
• Bではない : !B
• Aではない : !A
• A XOR B : !(!A || B) || !(A || !B)
• A XNOR B : !(!A || !B) || !(A || B)
• A : A
• B : B
• A NOR B : !(A || B)
• AはBを意味しない : !(!A || B)
• BはAを意味しない : !(!B || A)
• A AND B : !(!A || !B)
• 偽 : !(A || !A)

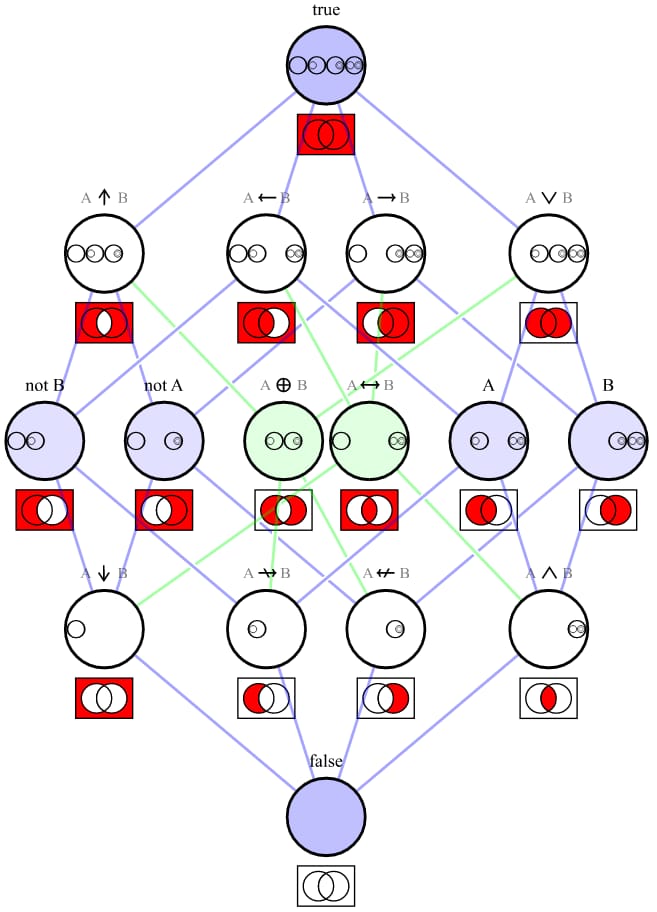
なお、NANDもNORもそれ自体で関数的に完全である（これは上記と同じ方法で証明できる）ので、ある演算子の集合が関数的に完全であることを検証したい場合は、その集合でNANDかNORのどちらかを表現できることを示せば十分である。

を示したグラフがこちらです。 ベン図 は、上記の各接続語について

[ ソース ]