[機械学習] ランダムフォレスト

2022-02-24 02:20:12

1 ランダムフォレストとは？

　　ランダムフォレスト（RF）は、新興の柔軟性の高い機械学習アルゴリズムとして、マーケティングから医療保険まで、マーケティングシミュレーションのモデル化、顧客源、保持、解約のカウント、患者の疾病リスクや感受性予測まで、幅広い用途に利用されています。当初、私は学外のコンペティションに参加する中で、ランダムフォレストのアルゴリズムに出会いました。近年の国内外のコンペティションでは、「2013 Baidu Campus Movie Recommendation System Competition」や「2014 Alibaba Tianchi Big Data Competition」、「The カグル・データサイエンス・コンペティション参加者のランダムフォレストの使用率はかなり高いです。また、個人的な知識ですが、防衛戦に進出したチームの多くも、ランダムフォレストやGBDTのアルゴリズムを選択しています。ということは、やはり精度の面ではランダムフォレストがかなり優れていることが分かります。

　　では、最後に「Random Forest」とはどのようなアルゴリズムなのでしょうか？

　　決定木に触れたことのある読者なら、ランダムフォレストがどんなものか理解するのは簡単だ。決定木を基本単位として、統合学習の考え方で複数の木を統合するアルゴリズムであり、本来はアンサンブル学習という機械学習の一分野である。ランダムフォレストという名前には2つのキーワードがあり、1つは「ランダム」、もう1つは「フォレスト」です。この例えは適切で、実はこれこそがランダムフォレストのメインアイデアであり、統合の具現化なのです。ランダム（random）の意味については、次章で説明します。

　　実際、直感的には、それぞれの決定木は分類器であり（分類の話をするとして）、1つの入力サンプルに対して、N本の木がN個の分類を持つことになる。そして、ランダムフォレストはすべての分類票を統合し、最も票を集めたカテゴリーを最終出力として指定するのですが、これがBaggingの最も単純な考え方の一つです。

2 ランダムフォレストの特徴

　　先に述べたように、ランダムフォレストは以下のような特徴を持つ、非常に柔軟で実用的な手法である。

現在のすべてのアルゴリズムの中で、精度の高さでは群を抜いている。
大規模なデータベースで効率的に実行できる／大規模なデータベースで効率的に実行できる。
数千の入力変数を変数削除なしで扱えます。
分類問題においてどの変数が重要であるかを推定することができる。
フォレスト構築の進行に伴い、汎化誤差の内部不偏推定値を生成する。
欠損データの推定に有効な方法を持ち、欠損データの割合が多い場合でも精度を維持できる。

　　実は、ランダムフォレストはこの6つの特徴だけでなく、機械学習におけるレザーマン（多芸者）に相当するもので、ほとんど何でも放り込むことができ、基本的に利用可能なのです。特に推論的なマッピングの推定に有効で、SVMほどパラメータのデバッグをする必要がないほどです。ランダムフォレストの詳細な紹介は、以下のランダムフォレストのホームページで見ることができます。ランダムフォレスト .

3 ランダムフォレストに関連する基礎知識

　　ランダムフォレストはよく理解されているように見えますが、その仕組みを完全に理解するには、機械学習に関連する多くの基礎知識が必要です。この記事では、一つ一つを確認するのではなく、簡単にお話しますので、あまり知らない方は、関連するブログ記事や他のブロガーの文献を参考にしてください。

1）情報、エントロピー、情報利得の概念

　　この3つの基本概念は、決定木の基本であり、分類に用いる特徴量を選択する際の順序を決定するための基礎となるものである。これらを理解すれば、決定木の概要を理解することができる。

　　シャノンの言葉を借りれば、情報とはランダムな不確実性を除去するために使われるものである。もちろんこれは古典的なものですが、それがどのようなものかはまだわかりにくいし、場所によって意味も違うかもしれません。機械学習における決定木の場合、カテゴリを持つものの集合が複数のクラスに分けられるとすると、あるクラス（xi）の情報は次のように定義できる。

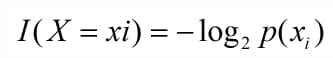
　　I(x)は確率変数の情報を表し、p(xi)はxiが発生する確率を表します。

　　エントロピーは不確実性の尺度として使われ、エントロピーが大きくなるほどx＝xiの不確実性は大きくなり、その逆もまた然りである。機械学習における分類問題では、エントロピーが大きいほど、カテゴリの不確実性が高くなり、その逆もまた然りである。

　　情報利得が大きい程、特徴の選択性が高い。

　　この点については、詳細が不明なので、興味のある学生は、以下を参照してください。情報量とエントロピーと情報利得このブログの記事

2) 決定木

　　決定木は、各内部ノードが属性のテスト、各ブランチがテスト出力、各リーフノードがカテゴリを表す木構造である。一般的な決定木アルゴリズムはC4.5, ID3, CARTである。

3）統合学習

　　統合学習は、複数のモデルを組み合わせて構築することで、一つの予測問題を解決するものである。これは、それぞれが独立して学習し、予測を行う複数の分類器／モデルを生成することで機能する。これらの予測は最終的に1つの予測に統合されるため、予測を行う単一の分類よりも優れた性能を発揮する。

　　ランダムフォレストは統合学習のサブクラスで、最終的な分類結果を決定するために決定木における投票選択に依存している。pythonで統合学習を実装するためのドキュメントはこちらで見ることができます。 Scikit学習ドキュメント .

4 ランダムフォレストの生成

　　前述したように、ランダムフォレストには多くの分類木が存在する。入力サンプルを分類するためには、それぞれの木に入力サンプルを入力して分類する必要がある。例えるなら，森の中である動物がネズミなのかリスなのかを議論する会議が開かれ，各木が独立して意見を表明する，つまり投票する必要がある．その投票によって、その動物がネズミなのかリスなのかが決められ、最も多くの票を集めた分類が森の分類の結果となる。森の中の木はそれぞれ独立しており、99.9％の無関係な木がすべてのシナリオをカバーする予測をし、その予測は互いに相殺される。少数の良い木の予測は、"noise"を超えて、良い予測になる。これがランダムフォレストのバギングという考え方です（バギングの重要なポイント：バギングのコストは、単一の決定木を使って予測をしないことであり、どの変数が重要な役割を果たしているかが不明となるため、バギングでは予測精度は向上しますが（The explanatory power is lost.）、損失が生じます。(従って、バギングは予測精度を向上させるが、説明力を失う。)。下図はその状況をグラフ化したものである。

　　木は並べ替えることができますが、森の中のそれぞれの木はどのように生成されるのでしょうか？

　　それぞれの木は、以下のルールに従って生成されます。

　　1) 訓練セットのサイズがNの場合，各木について，訓練セットからN個の訓練サンプルをランダムに，かつ解放して取り出し（このサンプリング方法をブートストラップサンプル法と呼ぶ），その木の訓練セットとする．

　　このことから、学習セットは木ごとに異なり、重複した学習サンプルが含まれていることがわかります（この点を理解することが重要です）。

なぜトレーニングセットをランダムにサンプリングするのか？(追記 @2016.05.28)

　　もし、ランダムサンプリングを行わず、すべてのツリーでトレーニングセットが同じであれば、最終的な学習済みツリーの分類結果はまったく同じになり、その場合はバギングの必要はまったくありません。

なぜプットバックサンプリングが必要なのか？ (追記 @2016.05.28)

　　私の理解では、こうです。もしプットバックサンプリングがなければ，各ツリーはすべて交差のない異なるサンプルで訓練され，各ツリーが "bias"，すべて絶対に "one-sided"になるようにします（もちろん，これは正しくないかもしれませんが）．ランダムフォレストの最終的な分類ランダムフォレストの最終的な分類は、複数の木（弱い分類器）の投票に依存し、それは「均質」であるべきなので、それぞれの木を訓練するために全く異なる訓練セットを使用しても、最終的な分類結果には役立たない。

　　2) 各サンプルが特徴次元Mを持つ場合、定数m<<Mを指定し、M個の特徴からm個の特徴のサブセットをランダムに選択し、木が分裂するたびに、このm個の特徴から最適なものを選択する。

　　3) 各木は可能な限り最大に成長し、枝刈り工程はない。

　　冒頭で述べたランダムフォレストのquot;random"は、ここでいう2つのランダム性のことです。この2つのランダム性の導入は、ランダムフォレストの分類性能にとって非常に重要である。これらはランダムフォレストをオーバーフィットさせにくくし、ノイズに非常に強い（例えば、デフォルト値に対して鈍感である）ものにします。

ランダムフォレストの分類効果（エラー率）には、2つの要素が関係しています。

フォレスト内の任意の2本の木の相関：相関が大きいほどエラーレートは大きくなる。
Forestの各木の分類力：各木の分類力が強いほど、Forest全体のエラーレートが低くなる。

　　選択する特徴の数mを減らすと、それに応じて木の関連性と分類力が低下し、mを増やすと両方が向上します。つまり、ランダムフォレストの唯一のパラメータである最適なm（または範囲）をどのように選択するかが重要なのです。

5 袋小路外エラー率(oobエラー)

　　前述したように、ランダムフォレストを構築する際の重要な問題は、最適なmをどのように選択するかである。この問題を解決するために、我々は主にバッグ外誤差（oob error）を計算することに依存している。

　　ランダムフォレストの重要な利点の1つは、誤差の不偏推定値を得るために交差検証や独立したテストセットを使用する必要がないことである。つまり、誤差の不偏推定値を生成プロセス中に作成することができ、内部で評価することができるのである。

　　各ツリーを構築する際に、トレーニングセットに対して異なるブートストラップサンプルを使用することが分かっています（ランダムサンプリングとプットバックサンプリング）。つまり、各木（k番目の木について仮定）において、学習インスタンスの約1/3はk番目の木の生成に関与しておらず、それらはk番目の木のoobサンプルと呼ばれます。

　　そして、このようなサンプリング特性により、oob推定を行うことができ、それは以下のように計算される。

(注)サンプル単位

　　1) 各サンプルについて、それがoobサンプルであるツリーでどの程度分類されるかを計算する（ツリーの約1/3）。

　　2) 次に、そのサンプルの分類結果として単純多数決を使用します。

　　3) 最後に、サンプル総数に対する誤分類数の比率をランダムフォレストのoob誤分類率として使用する。

　　(原著論文 k番目の木の構築で取り残された各ケースをk番目の木に落とし込んで分類を得る。このようにして、テストセットの分類を得る実行終了時に、事例nがoobされるたびに最も多くの票を得たクラスをjとする。j が n の真のクラスと等しくない回数の割合を全ケースで平均したものが oob エラー推定値である。(これは多くのテストで不偏であることが証明されている)。

　　oobミススペシフィケーション率はランダムフォレストの汎化誤差の不偏推定値であり、その結果は膨大な計算を必要とするk-foldクロスバリデーションに近似している。

6 ランダムフォレストの仕組みの簡単な説明例

　　説明年齢、性別、最高学歴、産業、居住地という5つのフィールドから、ランダムフォレストがどのようにその人の所得水準を予測するのか。

　　所得水準:

　　　　バンド1：40,000ドル以下

　　　　バンド2：40,000ドル～150,000ドル

　　　　バンド3：150,000ドル以上

　　ランダムフォレストの各ツリーは、CART（カテゴリ回帰木）と考えることができます。ここでは、フォレスト内に5つのCARTツリーがあり、特徴の総数N=5、m=1とします（ここでは、各CARTツリーが異なる特徴に対応すると仮定します）。

　　CART 1 : 変数 Age

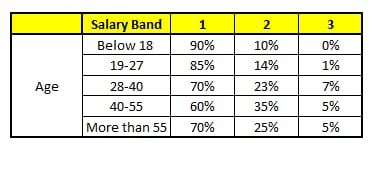
　　CART 2 : 変数 Gender

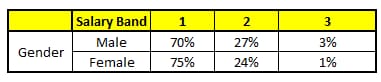
　　CART 3 : バリアブル教育

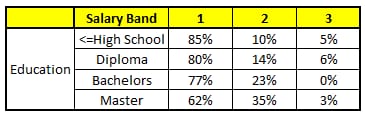
　　CART 4 : バリアブル・レジデンス

　　CART 5 : バリアブル産業

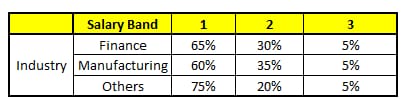
　　ある人物について予測したい情報は次の通りである。

　　1. 年齢 : 35歳 ; 2.性別: 男性; 3.最高学歴: 業種：製造業; 5.居住地：地下鉄。

　　これら5つのCARTツリーの分類結果をもとに、この人の情報の所得レベルの分布を作成することができます。

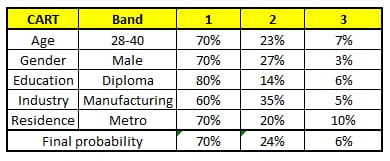
　　最終的に、この人は第1所得層が70％、第2所得層が約24％、第3所得層が6％という結論になり、この人は第1所得層（4万ドル未満）であるという判定になる。

7 PythonによるRandom Forestの実装

　　ランダムフォレストの実装には、pandasとscikit-learnという2つのPythonモジュールが使用されています。

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
import numpy as np

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['is_train'] = np.random.uniform(0, 1, len(df)) <= .75
df['species'] = pd.Factor(iris.target, iris.target_names)
df.head()

train, test = df[df['is_train']==True], df[df['is_train']==False]

features = df.columns[:4]
clf = RandomForestClassifier(n_jobs=2)
y, _ = pd.factorize(train['species'])
clf.fit(train[features], y)

preds = iris.target_names[clf.predict(test[features])]
pd.crosstab(test['species'], preds, rownames=['actual'], colnames=['preds'])

<イグ

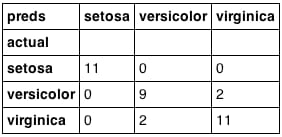
　　分類結果です。

　　他の機械学習分類アルゴリズムとの比較。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.lda import LDA
from sklearn.qda import QDA

h = .02 # step size in the mesh

names = ["Nearest Neighbors", "Linear SVM", "RBF SVM", "Decision Tree",
         "Random Forest", "AdaBoost", "Naive Bayes", "LDA", "QDA"]
classifiers = [
    KNeighborsClassifier(3),
    SVC(kernel="linear", C=0.025),
    SVC(gamma=2, C=1),
    DecisionTreeClassifier(max_depth=5),
    RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
    AdaBoostClassifier(),
    GaussianNB(),
    LDA(),
    QDA()]

X, y = make_classification(n_features=2, n_redundant=0, n_informative=2,
                           random_state=1, n_clusters_per_class=1)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)

datasets = [make_moons(noise=0.3, random_state=0),
            make_circles(noise=0.2, factor=0.5, random_state=1),
            linearly_separable
            figure]

figure = plt.figure(figuresize=(27, 9))
i = 1
# iterate over datasets
for ds in datasets:
    # preprocess dataset, split into training and test part
    X, y = ds
    X = StandardScaler().fit_transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4)

    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    xx, yy = np.meshgrid(np.range(x_min, x_max, h),
                         np.range(y_min, y_max, h))

    # just plot the dataset first
    cm = plt.cm.RdBu
    cm_bright = ListedColormap(['#FF0000', '#0000FF'])
    ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
    # Plot the training points
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
    # and testing points
    ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xticks(())
    ax.set_yticks(())
    i += 1

    # iterate over classifiers
    for name, clf in zip(names, classifiers):
        ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
        clf.fit(x_train, y_train)
        score = clf.score(X_test, y_test)

        # Plot the d

<イグ