ロジスティック回帰のエラー問題：警告メッセージ。1: glm.fit: アルゴリズムが集約されていない 2: glm.fit: 適合率が0か1の値で計算されている

ロジスティック回帰では、次の2種類の問題が報告されています。

警告: glm.fit: アルゴリズムが収束しませんでした。

警告: glm.fit: フィットした確率が数値的に0か1が発生しました。

警告メッセージ

1: glm.fit: アルゴリズムに集計がない 

2: glm.fit: 適合確率は0か1の値として計算される 

これはロジスティック回帰を行う際に比較的よくある問題で、なぜこのようなことが起こるのか、いくつか例を挙げてみましょう。

まず、glm関数の紹介です。

glm(formula, family=family.generator, data,control = list(...))

ファミリーを使用します。各応答分布（指数分布のファミリー）は、平均と線形予測器を関連付けるために様々な相関関数を可能にします。

 よく使われるファミリ

binomal(link='logit') ---- 応答変数は二項分布から提供され、リンク関数はlogit、すなわちロジスティック回帰。

binomal(link='probit') ---- 応答変数が二項分布、リンク関数がprobit

poisson(link='identity') ---- 応答変数がポアソン分布に従う、すなわち、ポアソン回帰

control:制御アルゴリズムの誤差と最大反復回数

glm.control(epsilon = 1e-8, maxit = 25, trace = FALSE)  

     -----maxit:アルゴリズムの最大反復回数、最大反復回数を変更する: control=list(maxit=100)

 glm関数を使用します。

library("ggplot2")
data<-iris[1:100,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata)
## Warning: glm.fit: algorithm did not converge
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -2.202e-05 -2.100e-08 -2.100e-08 2.100e-08 3.233e-05  
## Coefficients: -2.202e-05 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -97.30 87955.20 -0.001 0.999
## pl 39.56 34756.04 0.001 0.999
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1045e+02 on 79 degrees of freedom
## Residual deviance: 2.0152e-09 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 25

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata, control = list(maxit = 100))
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -8.134e-06 -2.110e-08 -2.110e-08 2.110e-08 1.204e-05  
## Coefficients: -8.134e-06 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -106.14 237658.98 0 1
## pl 43.16 93735.01 0 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1070e+02 on 79 degrees of freedom
## Residual deviance: 2.7741e-10 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 27

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col='predict')

testdata$y <- c(1:80)
qplot(pl,y,data =testdata,colour =factor(species))

data<-iris[51:150,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~sw+pw,binomial(link='logit'),data=testdata)
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ sw + pw, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -1.68123 -0.12839 -0.01807 0.07783 2.24191  
 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -12.792 5.828 -2.195 0.028168 *  
## sw -4.214 1.970 -2.139 0.032432 *  
## pw 15.229 3.984 3.823 0.000132 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## (Dispersion parameter for binomial family taken to be 1) 
## Null deviance: 110.854 on 79 degrees of freedom
## Residual deviance: 21.382 on 77 degrees of freedom
## AIC: 27.382
## Number of Fisher Scoring it ## 
## Number of Fisher Scoring iterations: 7

なお、glm関数でロジスティック回帰を行った場合、警告が表示されます。

警告メッセージ
1: glm.fit: アルゴリズムに集計を行わない 
2: glm.fit:適合確率は0または1の値として計算される

また、両係数のp値は0.999であり、回帰係数は有意でないことがわかる。

最初の注意点は、アルゴリズムが収束しないことです。
     glm関数の最大反復回数maxit=25。データが良くない場合、25回繰り返してもアルゴリズムが収束しないことがあるので、繰り返し回数を増やして収束しない問題を解決しようとします。しかし、反復回数を増やしてもアルゴリズムが収束しない場合は、本当にデータが悪いので、特異値チェックなどのさらなる処理が必要です。

p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col="response")

x3<-seq(1.5,4,length=80)
y3<-(4.284/15.656)*x3+13.447/15.656
aaa<-data.frame(x3,y3)

p <- ggplot()
p+geom_point(data = testdata,aes(x=sw,y=pw,colour=factor(species)))+
geom_line(data = aaa,aes(x = x3,y = y3,colour="line"))

summary(lgst)

## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata, control = list(maxit = 100))
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -8.134e-06 -2.110e-08 -2.110e-08 2.110e-08 1.204e-05  
## Coefficients: -8.134e-06 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -106.14 237658.98 0 1
## pl 43.16 93735.01 0 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1070e+02 on 79 degrees of freedom
## Residual deviance: 2.7741e-10 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 27

上記と同様に、最初の警告は反復回数を増やすことで解決し、その時点でアルゴリズムは収束する。

しかし、2つ目の警告が残り、回帰係数P = 1はまだ有意ではありません。

2つ目の警告：適合確率は0または1として計算される

まず、この警告は何を意味するのでしょうか？
まず、学習サンプルのロジスト回帰の結果を見てみましょう。提案された各サンプルが「セトサ」クラスに属する確率は何％でしょうか？

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

p<-predict(lgst,type='response')
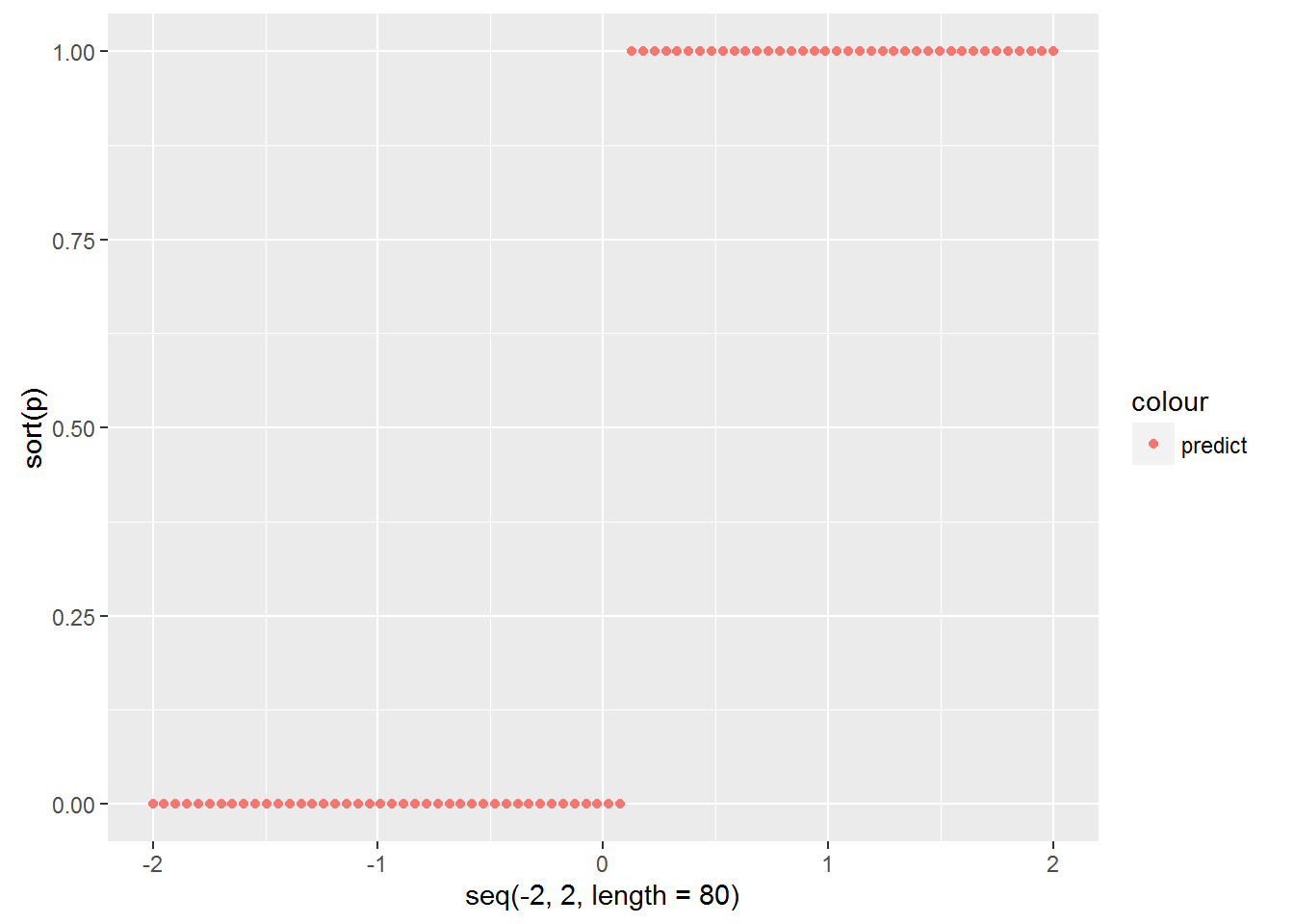
qplot(seq(-2,2,length=80),sort(p),col='predict')

<イグ

学習サンプルが「セトーサ」クラスである確率はほぼ0かほぼ1であり、ロジスティックモデルに期待されるS字カーブではないことがおわかりいただけると思います。これが2つ目の注意点です。

  では、なぜこのようなことが起こるのか、ということです。
 (以下は、高麗人参検定の説明の一部を個人的に理解したに過ぎない)

  これは一種のオーバーフィットと解釈でき、回帰係数の最適化探索過程で、あるクラスに属するカテゴリ（y=1）の線形適合度が大きくなり、別のクラスに属するカテゴリ（y=0）の線形適合度はデータにより小さくなる傾向がある。

回帰係数を解く、つまり回帰係数が探索過程で尤度関数を極限化するため、極限尤度推定の原理が使われる。

つまり、探索過程のバイアスは、h(x)がy=1では大きく、y=0では小さくなる傾向があるということですね。

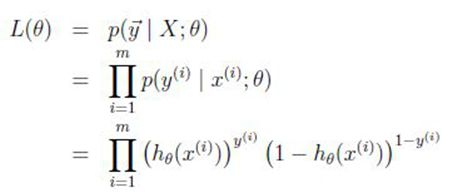
つまり、係数Θは、Y=1クラスでは-ΘTXが大きくなり、Y=0クラスでは-ΘTXが小さくなる傾向がある。この結果、P(y=1|x;Θ)-->1; P(y=0|x;Θ)-->0 ...となる。

そこでまた疑問なのですが、どのようなデータであれば、このようなオーバーフィッティングが起こるのでしょうか？

 まず、上のロジスティック回帰を、setosaとversicolorという種のpl値のサンプルについて見てみましょう（横軸はpl値で、plのサンプルデータ点が重ならないように、無関係なy値を加えてサンプル点を拡張しています）。

testdata$y <- c(1:80)
qplot(pl,y,data =testdata,colour =factor(species))

<イグ

2種類のデータが明らかに完全に線形分離可能であることがわかります。

したがって、回帰係数探索の過程で一変量線形関数h(x)の傾きの絶対値を大きくすることで、h(x)がy=1クラスでは大きく、y=0クラスでは小さくなる傾向を実現することができるのです。

つまり、サンプルデータが完全に分割可能な場合、ロジスティック回帰はしばしばオーバーフィッティングの問題、すなわち、適合した確率が0か1になるように働くという第2の警告を引き起こすのです。

ロジスティックモデルは、2回目の警告以降の予測には適さないことが多い。このような線形分離可能なサンプルデータに対しては、直接的なルールベースの判定（例えば、pl<2.5ならセトーサクラス、pl>2.5ならバーシカロールクラス）を用いることがシンプルで好適であると言えます。

以下では、不完全に分離可能な2次元の学習データに対するロジスティック回帰の処理について示す。

data<-iris[51:150,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~sw+pw,binomial(link='logit'),data=testdata)
summary(lgst)

## 
## Call:
## glm(formula = testdata$species ~ sw + pw, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -1.68123 -0.12839 -0.01807 0.07783 2.24191  
 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -12.792 5.828 -2.195 0.028168 *  
## sw -4.214 1.970 -2.139 0.032432 *  
## pw 15.229 3.984 3.823 0.000132 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## (Dispersion parameter for binomial family taken to be 1) 
## Null deviance: 110.854 on 79 degrees of freedom
## Residual deviance: 21.382 on 77 degrees of freedom
## AIC: 27.382
## Number of Fisher Scoring it ## 
## Number of Fisher Scoring iterations: 7

提案された確率曲線。(基本的にロジスティックモデルのS字カーブに合致します。）

p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col="response")

<イグ

トレーニングサンプルの散布図と分類の境界線。

(ロジスティック回帰の分類境界を描く、つまり曲線h(x)=0.5を描く)

x3<-seq(1.5,4,length=80)
y3<-(4.284/15.656)*x3+13.447/15.656
aaa<-data.frame(x3,y3)

p <- ggplot()
p+geom_point(data = testdata,aes(x=sw,y=pw,colour=factor(species)))+
geom_line(data = aaa,aes(x = x3,y = y3,colour="line"))

<イグ

 内容は、元のブロガーが参照したものですが、印象を深めるために、自分でもう一度、図をggplot2に置き換えてやってみました、元の参照先は以下のリンクです。