[解決済み] 再帰的関数の空間複雑性

質問

以下のような関数がある。

int f(int n) {
  if (n <= 1) {
    return 1;
  }
  return f(n - 1) + f(n - 1);
} 

私は、ビッグ・オー時間複雑性が O(2^N) というのも、それぞれの呼び出しが関数を2回呼び出すからです。

私が理解できないのは、なぜスペース/メモリの複雑さが O(N) ?

解決方法は？

この種の問題へのアプローチとして有効なのは 再帰木 . 見極めるべき再帰関数の特徴は、次の2つです。

1. ツリーの深さ 戻り値 は基本ケースまで実行されます)
2. ツリーの幅 再帰的な関数呼び出し される)

この場合の再帰関係式は T(n) = 2T(n-1) . あなたが正しく指摘したように、時間の複雑さは O(2^n) が、再帰木との関係で見てみましょう。

      C
     / \         
    /   \      
T(n-1)  T(n-1)

            C
       ____/ \____
      /           \
    C              C   
   /  \           /  \
  /    \         /    \
T(n-2) T(n-2) T(n-2)  T(n-2)

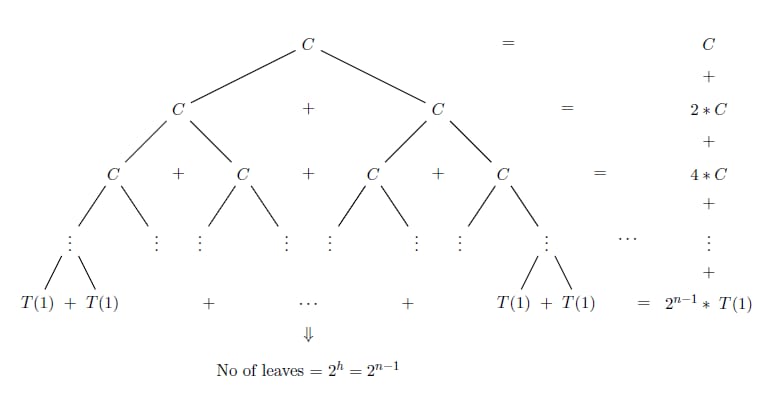
このパターンは、次の画像のようなベースケースになるまで続きます。

ツリーのレベルが上がるごとに、nは1ずつ減少します。 nの深さ 基本ケースに到達する前に 各ノードには2つの分岐があり、レベルの総数はn個なので、ノードの総数は次のようになります。 2^n となり、時間計算量は O(2^n) .

各関数呼び出しはプログラムスタックに格納されるため、我々のメモリの複雑さは return 文の数で決まります。一般化すると、再帰的な関数のメモリ複雑度は O(recursion depth) . ツリーの深さが示すように、合計で n 個の return 文を持つことになるので、メモリの複雑度は O(n) .