[解決済み] gluSphere()を使用せずにOpenGLで球体を描画する？

質問

を使わずにOpenGLで球体を描画する方法を説明したチュートリアルはありますか？ gluSphere() ?

OpenGLの3Dチュートリアルの多くは、立方体に関することだけです。私は検索しましたが、球を描くための解決策のほとんどは、球を描画するために gluSphere() . また、球体を描くためのコードを掲載しているサイトもあります。 このサイト しかし、球体を描くための数学的な説明はない。また、そのリンク先には4角形ではなくポリゴンで球体を描く方法の他のバージョンもあります。しかし、やはり、そのコードで球体がどのように描かれるのか理解できません。必要であれば、球体を修正できるように視覚化できるようにしたいのです。

どのように解決するのですか？

一つの方法として、三角形の辺を持つプラトニックな立体、つまり 八面体 例えば そして、それぞれの三角形を、再帰的に小さな三角形に分割していきます。

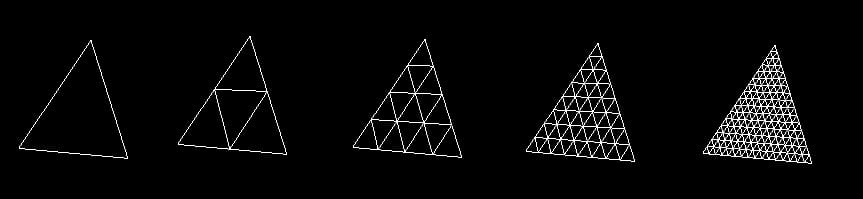
十分な数の点が得られたら、それらの点のベクトルを正規化し、ソリッドの中心からの距離がすべて一定になるようにする。そうすると、点の数が増えるにつれて、側面が球体のように膨らみ、滑らかさが増す。

ここでいう正規化とは、ある点を移動させ、他の点との角度を同じにし、その間の距離を異ならせることである。 2次元の例です。

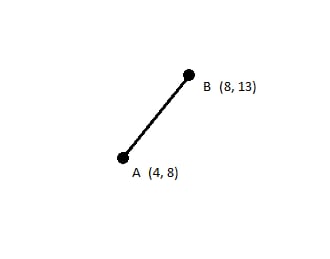
AとBは6単位離れている。しかし、Aから12ユニット離れた線分AB上の点を見つけたいとする。

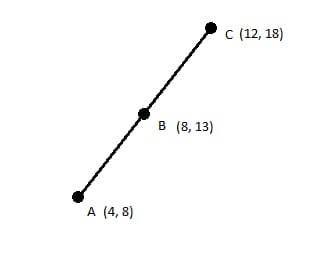
CはAを基準にしてBを距離12で正規化した形と言える。Cは次のようなコードで得ることができる。

#returns a point collinear to A and B, a given distance away from A. 
function normalize(a, b, length):
    #get the distance between a and b along the x and y axes
    dx = b.x - a.x
    dy = b.y - a.y
    #right now, sqrt(dx^2 + dy^2) = distance(a,b).
    #we want to modify them so that sqrt(dx^2 + dy^2) = the given length.
    dx = dx * length / distance(a,b)
    dy = dy * length / distance(a,b)
    point c =  new point
    c.x = a.x + dx
    c.y = a.y + dy
    return c

この正規化処理を、同じ点Aを基準にして、同じ距離Rのたくさんの点に対して行うと、正規化された点はすべて中心A、半径Rの円の弧上に位置することになります。

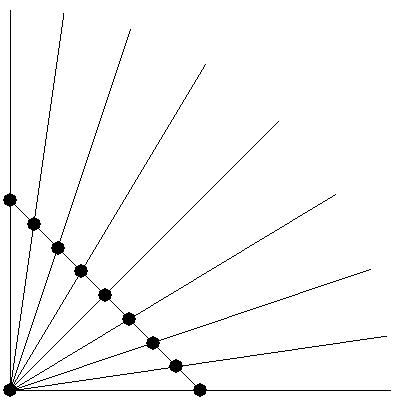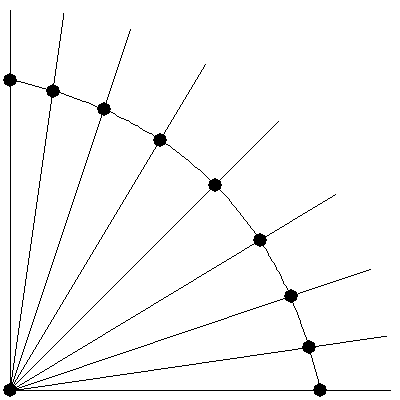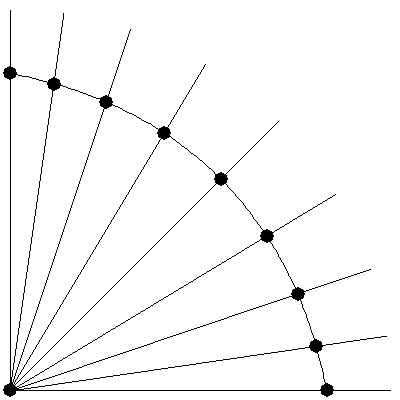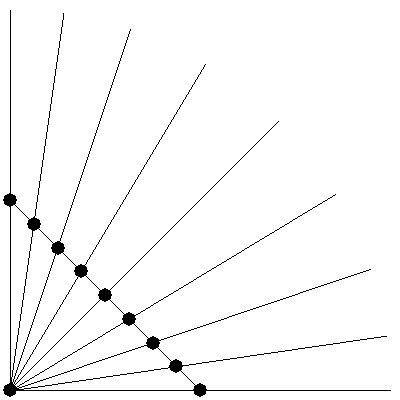
ここでは、黒い点は直線から始まり、円弧に膨らんでいます。

この処理は3次元に拡張することができ、その場合は円ではなく球になる。正規化関数にdz成分を追加するだけです。

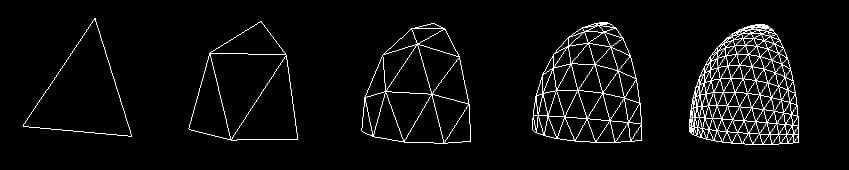
で球体を見ると エプコット これは正12面体で、丸く見せるために面が膨らんでいるのです。