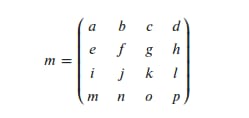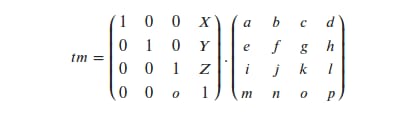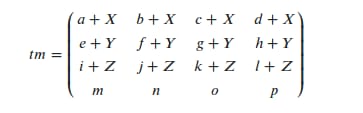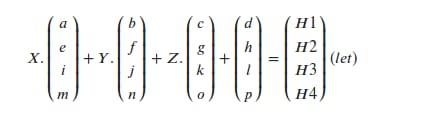[解決済み] GLMは翻訳をどのように扱うか

質問

OpenGLの数学ライブラリ(GLM)は、以下のアルゴリズムで並進行列を計算します。

//taken from source code
template<typename T, qualifier Q>
GLM_FUNC_QUALIFIER mat<4, 4, T, Q> translate(mat<4, 4, T, Q> const& m, vec<3, T, Q> const& v)
{
    mat<4, 4, T, Q> Result(m);
    Result[3] = m[0] * v[0] + m[1] * v[1] + m[2] * v[2] + m[3];
    return Result;
}

(ここでは、ベクトル v は 3 次元ベクトル、行列 m は 4X4 の行列で、同次座標を使用しているので、ベクトル v も4次元である）。

以下は、「線形代数理論」からの引用です。

とする。 m には項目があります。

ここで、行列 m は何らかの線形変換を与えるもので、変換行列でもある。そして、X、Y、Zの次元にそれぞれX、Y、Zの並進を加えたい。私の記憶が間違っていなければ、その方法は合成行列を作ることである。

のようなものが得られます。

さて、このGLMのtranslateという関数が何をするものなのか、よくわかりません。

そして、並進の変換を加えた行列、すなわちmは次のようになる。

さて、この2つの行列は等しくないので、異なる変換になります。そこで、どちらの行列が実際の変換を行うのか、どちらが正しいのか、あるいは、アルゴリズムの背後に他のアイデアが隠されているのか、混乱しています。

注意：答えを読む前に、行列の列メジャー表現では、次のように行列のエントリにアクセスすることに注意してください：行列[列インデックス][行インデックス]。 .

編集

変換を行うソースコードです。

#include <iostream>
#include <GL/glew.h>
#include <GLFW/glfw3.h>
#include <cmath>
#include <string.h>

#include "glm/glm.hpp"
#include "glm/gtc/matrix_transform.hpp"
#include "glm/gtc/type_ptr.hpp"


// Window Dimensions
const GLint WIDTH=800, HEIGHT=600;
GLuint VAO, VBO, shader;
GLint uniformModel {};
GLint uniformModelRot {};
GLfloat triOffset {};
float triMaxOffset = 0.7f;
bool direction = true;
const float toRadians =  3.14159265f/180.0f;


// vertex shader
static const char* vShader = 
"#version 330\n"
"layout (location = 0) in vec3 pos;\n"
"uniform mat4 model;\n"
"void main(){\n"
"   gl_Position = model * vec4(0.5*pos, 1.0);\n"
"}\n";

// fragment shader
static const char* fShader = ""
"#version 330\n"
"out vec4 color;\n"
"uniform mat4 model;\n"
"void main(){\n"
"   color = model *vec4(1.0, 1.0, 0.0, 1.0);\n"
"}\n";

void AddShader(GLuint theProgram, const char* ShaderCode, GLenum shaderType, std::string info){
    std::cerr <<"INFO: Adding "<<info<<" Shader"<<std::endl;
    GLuint theShader = glCreateShader(shaderType);

    const GLchar* theCode[1];
    theCode[0] = ShaderCode;

    GLint codeLength[1];
    codeLength[0] = strlen(ShaderCode);

    glShaderSource(theShader, 1, theCode, codeLength);
    glCompileShader(theShader);

    GLint result =0;
    GLchar eLog[1024] ={0};

    glGetShaderiv(theShader, GL_COMPILE_STATUS, &result);
    if(!result){
        glGetShaderInfoLog(shader, sizeof(eLog), NULL, eLog);
        std::cerr<<"Error compiling program"<<std::endl;
        return;
    }
    glAttachShader(theProgram, theShader);

}

void CompileShader(){
    shader = glCreateProgram();
    if(!shader){
        std::cerr<<"Error creating shader"<<std::endl;
        return;
    }

    AddShader(shader, vShader, GL_VERTEX_SHADER, "vertex");
    AddShader(shader, fShader, GL_FRAGMENT_SHADER, "fragment");

    GLint result =0;
    GLchar eLog[1024] ={0};

    glLinkProgram(shader);
    glGetProgramiv(shader, GL_LINK_STATUS, &result);
    if(!result){
        glGetProgramInfoLog(shader, sizeof(eLog), NULL, eLog);
        std::cerr<<"Error linking program"<<std::endl;
        return;
    }

    glValidateProgram(shader);
    glGetProgramiv(shader, GL_VALIDATE_STATUS, &result);
    if(!result){
        glGetProgramInfoLog(shader, sizeof(eLog), NULL, eLog);
        std::cerr<<"Error Validating program"<<std::endl;
        return;
    }

    uniformModel = glGetUniformLocation(shader,"model");

}

void CreateTriangles(){
    GLfloat vertices[]={
        -1.0f, -1.0f, 0.0f,
        1.0f, -1.0f, 0.0f,
        0.0f, 1.0f, 0.0f
    };

    glGenVertexArrays(1, &VAO);
    glBindVertexArray(VAO);

        glGenBuffers(1, &VBO);
        glBindBuffer(GL_ARRAY_BUFFER, VBO);
        glBufferData(GL_ARRAY_BUFFER, sizeof(GLfloat)*9,vertices, GL_STATIC_DRAW);
        glVertexAttribPointer(0,3,GL_FLOAT,GL_FALSE,0,0);
        glEnableVertexAttribArray(0);

    glBindBuffer(GL_ARRAY_BUFFER, 0);
    glBindVertexArray(0);
}


int main(){
    //initialize GLFW
    if(!glfwInit()){
        std::cerr << "GLFW initialization failed!" << std::endl;
        glfwTerminate();
        return 1;
    }

    //Setup GLFW window properties
    //openGL version
    glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
    glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
    // core profile = no backward compatibility
    glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
    //allow forward compatibility
    glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);

    GLFWwindow *mainWindow = glfwCreateWindow(WIDTH, HEIGHT, "TEST WINDOW", NULL, NULL);

    if(!mainWindow){
        std::cerr << "GLFW Window creation failed" << std::endl;
        glfwTerminate();
        return 1;
    }

    // get Buffer size information
    int bufferWidth, bufferHeight;
    glfwGetFramebufferSize(mainWindow, &bufferWidth, &bufferHeight);
    // set context for GLEW to use
    glfwMakeContextCurrent(mainWindow);

    // allow modern extension features

    if(glewInit()!=GLEW_OK){
        std::cerr << "GLEW initialization failed" << std::endl;
        glfwDestroyWindow(mainWindow);
        glfwTerminate();
        return 1;
    }

    // setup viewport size
    glViewport(0, 0, bufferWidth, bufferHeight);
    CreateTriangles();
    CompileShader();




    while(!glfwWindowShouldClose(mainWindow)){
        // get and handle user input events
        glfwPollEvents();

        glClearColor(1.0f, 0.0f, 0.0f, 1.0);
        glClear(GL_COLOR_BUFFER_BIT);

        if(direction){
            triOffset += 0.05f;
        }else{
            triOffset -= 0.05f;
        }

        if(abs(triOffset) >= triMaxOffset){
            direction = !direction;
        }

        glUseProgram(shader);

        glm::mat4 modelMatrix(1.0f); 
        modelMatrix = glm::translate(modelMatrix, glm::vec3(triOffset, 0.0f, 0.0f));

        glUniformMatrix4fv(uniformModel, 1, GL_FALSE,glm::value_ptr(modelMatrix));
            glBindVertexArray(VAO);
                glDrawArrays(GL_TRIANGLES,0,3);
            glBindVertexArray(0);
        glUseProgram(0);
        // swap buffers
        glfwSwapBuffers(mainWindow);
    }

    return 0;
}

解決方法は？

OpenGL数学(GLM) がベースになっています。 OpenGLシェーディング言語(GLSL) . 何 glm::translate 実際に行うのは、翻訳行列を設定し、入力行列に翻訳を乗じることです。これは m*t の意味で GLSL ベクトルおよびマトリックス演算 :

mat<4, 4, T, Q> Result(m);
Result[3] = m[0] * v[0] + m[1] * v[1] + m[2] * v[2] + m[3];

(以下では Result で代用されます。 R )

注 m[0] * v[0] の各要素を乗算します。 m[0] をスカラー v[0] . その結果、ベクトル (m[0][0]*v[0], m[0][1]*v[0], m[0][2]*v[0], m[0][3]*v[0]) .

だから R[3] = m[0]*v[0] + m[1]*v[1] + m[2]*v[2] + m[3] と同じです。

R[3][0] = m[0][0] * v[0] + m[1][0] * v[1] + m[2][0] * v[2] + m[3][0]
R[3][1] = m[0][1] * v[0] + m[1][1] * v[1] + m[2][1] * v[2] + m[3][1]
R[3][2] = m[0][2] * v[0] + m[1][2] * v[1] + m[2][2] * v[2] + m[3][2]
R[3][3] = m[0][3] * v[0] + m[1][3] * v[1] + m[2][3] * v[2] + m[3][3]

glm::translate を実際に計算します。

vh = (v[0], v[1], v[2], 1)
R = m
R[3][0] = dot( (m[0][0], m[1][0], m[2][0], m[3][0]), vh )
R[3][1] = dot( (m[0][1], m[1][1], m[2][1], m[3][1]), vh )
R[3][2] = dot( (m[0][2], m[1][2], m[2][2], m[3][2]), vh )
R[3][3] = dot( (m[0][3], m[1][3], m[2][3], m[3][3]), vh )

上記のコードでは ドット積 の行の m による vh . vh は翻訳文の4段目 t . 翻訳行列に注目 t は次のように定義される。

     c0  c1  c2  c3 
---------------------  
r0:   1   0   0  v[0]  
r1:   0   1   0  v[1]
r2:   0   0   0  v[2]
r3:   0   0   0  1  

4x4 の行列を連結したもの ( R = m*t )は ドット積 の行の m の列と t と表現することができる。 (参照 OpenGL Shading Language 4.60 仕様 - 5.10. ベクトルと行列の操作 )

for i from 0 to 3
    for j fro 0 to 3
        R[i][j] = dot( (m[0][j], m[1][j], m[2][j], m[3][j]), t[i] )

ここで dot(a, b) == a[0]*b[0] + a[1]*b[1] + a[2]*b[2] + a[3]*b[3] ,
(m[0][j], m[1][j], m[2][j], m[3][j]) は j -の1行目 m と
t[i] は i -の第 1 列目。 t .

について glm::translate をコピーすれば十分です。 R[0] , R[1] と R[2] から m[0] , m[1] と m[2] .

例：( i=0 , j=0 ):

R[0][0] = dot( (m[0][0], m[1][0], m[2][0], m[3][0]), t[0] )
R[0][0] = dot( (m[0][0], m[1][0], m[2][0], m[3][0]), (1, 0, 0, 0) )
R[0][0] = m[0][0] * 1 + m[1][0] * 0 + m[2][0] * 0 + m[3][0]) * 0
R[0][0] = m[0][0]

GLM 行列は（OpenGL行列として）列の主要な順序で保存されます。デバッガで行列を調査する場合、それは混乱を招くかもしれません。

行列がある場合

     c0  c1  c2  c3 
-------------------  
r0:  Xx  Yx  Zx  Tx  
r1:  Xy  Yy  Zy  Ty 
r2:  Xz  Yz  Zz  Tz  
r3:   0   0   0   1  

とすると、4*4 の OpenGL マトリックスのメモリイメージは次のようになります。

Xx, Xy, Xz, 0, Yx, Yy, Yz, 0, Zx, Zy, Zz, 0, Tx, Ty, Tz, 1

デバッガで調べると、次のようになることがあります。

[ [ Xx, Xy, Xz, 0 ],
  [ Yx, Yy, Yz, 0 ],
  [ Zx, Zy, Zz, 0 ],
  [ Tx, Ty, Tz, 1 ] ]