スマートプログレスバー ETA計算

質問

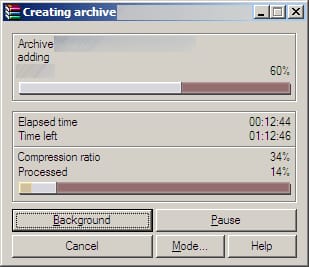
多くのアプリケーションで、ファイルのダウンロード、圧縮タスク、検索などのプログレス バーがあります。私たちは皆、何かが起こっていることをユーザーに知らせるために、しばしばプログレス バーを使用します。そして、どれだけの作業が行われたか、どれだけの作業が残っているかなどの詳細を知っていれば、現在の進捗レベルに到達するまでにかかった時間から外挿することで、時間の見積もりを行うこともできます。

_{(ソース jameslao.com )}

しかし、この Time Left "ETA" 表示が滑稽なほど悪いプログラムも見てきました。ファイル コピーが 20 秒で完了すると主張し、1 秒後に 4 日かかると表示され、その後また 20 分と表示されます。 役に立たないだけでなく、混乱しますよ。 ETA がこれほど変化する理由は、進行速度自体が変化し、プログラマーの計算が過敏になる可能性があるからです。

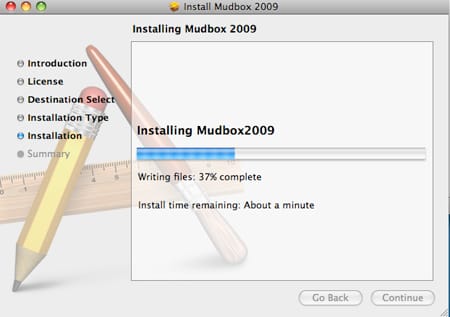
Apple は、正確な予測を避け、漠然とした見積もりを出すだけで、これを回避しています!

_{(ソース autodesk.com )}

それも困る、ちょっと休憩する時間はあるのか、それともあと2秒でタスクが終わるのか。予測があやふやだと、予測をすること自体が無意味になってしまいます。

簡単だけど間違った方法

ETA計算の第一段階として、おそらく誰もが、すでに終わった割合をp、これまでにかかった時間をtとすると、終了までにかかる時間の推定値としてt*(1-p)/pを出力するという関数を作るだけでしょう。 この単純な比率は "OK"動作しますが、特に計算の終盤では恐ろしいことになります。遅いダウンロード速度で一晩中コピーがゆっくりと進み、最終的に朝になって何かが作動してコピーが 100 倍の速度でフル回転し始めた場合、90% 完了時の ETA は 1 時間と表示され、10 秒後に 95% に到達して ETA は 30 分と表示されますが、これは明らかに恥ずかしくなるほどの推測です... この場合、10 秒というのははるかに、はるかに、優れた推測です。

このような場合、計算を変更することができます。 最近の を使用するように計算を変更するとよいでしょう。過去 10 秒間の平均ダウンロード レートまたは完了レートを取り、そのレートを使用して完了までの時間を予測するのです。この方法は、先ほどの一晩でダウンロードが完了し、最後にスピードアップした例では、最後に非常に良い完了予測が得られるので、非常に良いパフォーマンスです。 しかし、これにはまだ大きな問題があります。それは、レートが短時間で急激に変化すると、ETA が乱高下し、「20 秒で完了、2 時間で完了、2 秒で完了、30 分で完了」 というプログラミングの恥をさらすような急激な表示が行われることです。

実際の質問です。

計算の時間履歴がある場合、タスクの完了の推定時間を計算する最良の方法は何ですか？ 私は、GUI ツールキットや Qt ライブラリへのリンクを探しているわけではありません。 私が尋ねているのは アルゴリズム について尋ねているのです。

数学の公式で成功したことがありますか。 ある種の平均化、たとえば、10 秒間のレートと 1 分間のレートと 1 時間間のレートの平均を使用するとか? 新しい推定値が前の推定値から大きく変動した場合、それを調整し、あまりバウンドさせないようにする、といった人工的なフィルタリング？進捗と時間経過を統合して、完了時の統計的エラーメトリクスを与えるためにレートの標準偏差を見つけるような、ある種の空想的な履歴分析？

何を試して、何が一番効果的でしたか？

どのように解決しましたか？

オリジナルの回答

このサイトを作成した会社 を作っているようです。 というスケジューリングシステムを作っているそうです。その仕組みは、過去に基づく未来のモンテカルロ・シミュレーションです。

付録 モンテカルロ法の説明

このアルゴリズムがあなたの状況でどのように機能するかです。

あなたは、タスクを一連のマイクロタスク、たとえば1000個としてモデル化します。1 時間後、あなたはそのうちの 100 個を完了したとします。ここで、完了した 90 個のマイクロタスクをランダムに選択し、それらの時間を加算して 10 を乗じることで、残りの 900 ステップについてシミュレーションを実行します。これをN回繰り返すと、残り時間の推定値がN個得られます。これらの見積もり時間の平均は約9時間です。しかし、結果として得られる分布をユーザーに提示することで、「90%の確率で、あと3～15時間かかる」など、確率を正直に伝えることができます。

このアルゴリズムは、定義上、問題のタスクが一連の 独立した、ランダムな マイクロタスクの束としてモデル化できる場合、このアルゴリズムは完全な結果を生成します。たとえば、インストーラーには通常、ダウンロード/解凍/インストールというタスクリストがあり、一方の速度は他方を予測できません。

付録 モンテカルロの簡略化

私は統計学の第一人者ではありませんが、この方法でのシミュレーションをよく見てみると、独立した多数の確率変数の和として必ず正規分布が返されると思います。したがって、それを実行する必要は全くありません。実際、完了した回数をすべて記憶しておく必要もなく、その合計と二乗の合計だけが必要だからです。

あまり標準的な表記ではないかもしれませんが

sigma = sqrt ( sum_of_times_squared-sum_of_times^2 )
scaling = 900/100          // that is (totalSteps - elapsedSteps) / elapsedSteps
lowerBound = sum_of_times*scaling - 3*sigma*sqrt(scaling)
upperBound = sum_of_times*scaling + 3*sigma*sqrt(scaling)

これで、今から[lowerBound, upperBound]の間に、ある一定の確率（95%程度のはずですが、おそらく何かの定数要素を見落としたのでしょう）で終了する、というメッセージを出力することができます。