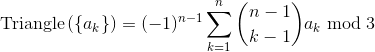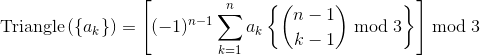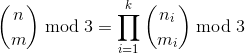[解決済み] 3色の三角形

質問

この問題に対するコードを作ろうとしています。

(出典 https://www.codewars.com/kata/insane-coloured-triangles/train/c )

色の三角形は、それぞれの色の列から作成されます。 赤、緑、青のいずれかになります。連続した行は、それぞれ1つ少ない色で構成されています。 最後に触れた2色を考慮して生成されます。 を、前の行の これらの色が同じであれば、同じ色 が新しい行に使われます。異なる場合は、欠落した色が新しい行に使用されます。 新しい行で使用されます。これを、最後の行が完成するまで続けます。 が1色で生成される。

例えば、異なる可能性としては

Colour here:            G G        B G        R G        B R 
Becomes colour here:     G          R          B          G 

With a bigger example:
   R R G B R G B B  
    R B R G B R B
     G G B R G G
      G R G B G
       B B R R
        B G R
         R B
          G

三角形の最初の行が文字列として与えられ、下の行に表示される最終的な色を文字列として返すのがあなたの仕事である。上の例では、次のように与えられる。 'RRGBRGBB' を返さなければなりません。 'G' .

制約事項です。

1 <= length(row) <= 10 ** 5

入力文字列には、大文字の ' B', 'G' or 'R' .

正確なテストケースの数は以下のようになります。

100 tests of 100 <= length(row) <= 1000 
100 tests of 1000 <= length(row) <= 10000 
100 tests of 10000 <= length(row) <= 100000

例

triangle('B') == 'B'
triangle('GB') == 'R'
triangle('RRR') == 'R'
triangle('RGBG') == 'B'
triangle('RBRGBRB') == 'G'
triangle('RBRGBRBGGRRRBGBBBGG') == 'G'

このコードを作成し、すべてのサンプルテイストで動作するようになりましたが length of row > 25 の長さになる場合があり、失敗します。 100,000 この問題を解決するために何か提案があれば、少なくとも問題を解決できる数学的な公式や小さなヒントがあれば教えてください。

ちなみにこのコードは、このサイトで問題を解決する数学的な方法を見つけた後に作りました。

https://math.stackexchange.com/questions/2257158/three-color-triangle-challenge

long long factorial(long long num)     
{
    long long fact = num;

    if (fact == 0)
        fact = 1;

    while (num > 1)
    {
        num--;
        fact *= num;
    }
    return (fact);
}

long long combination(long long n, long long k, long long fact_n)
{
    long long fact_k = factorial(k);
    long long comb = ( fact_n / (fact_k * factorial(n - k)) );
    return (comb);
}

char triangle(const char *row)
{
    long long len = strlen(row);
    long long n = len - 1;
    long long k = 0;
    int sign = pow(-1,n);
    long long sum = 0;
    char *result = "RGB";
    int a;
    long long fact_n = factorial(n);

    while (k < len)                 //This while calculate Segma (∑). 
    {
        if (row[k] == 'R')
            a = 0;
        else if (row[k] == 'G')
            a = 1;
        else if (row[k] == 'B')
            a = 2;

        if (a != 0)
            sum = sum + (combination(n,k,fact_n) * a); 
        k++;
    }

    sum = sign * (sum % 3);

    if (sum == -1 || sum == -2)
        sum += 3;

  return (result[sum]);
}

解決方法は？

ご提示いただいたリンク先の計算式が正しいものとします。

整数のオーバーフローを回避するために、以下を適用する必要があります。 モジュロ演算規則 :

(a * b) mod c = ((a mod c) * (b mod c)) mod c

(a ± b) mod c = ((a mod c) ± (b mod c)) mod c

数式に適用する。

しかし、どのように計算するのでしょうか？

... 係数そのものを直接計算することなく（オーバーフローを引き起こす可能性がある）？

3は素数なので、これを実現するためには ルーカスの定理 :

... ここで n_i, m_i は i -の第 n, m で ベース3 .

Base-3への変換は、整数の割り算で簡単にできます。

// convert a number to base 3
// and returns the number of digits
unsigned conv_base_3(unsigned n, unsigned max, unsigned* out)
{
    unsigned i = 0;
    while (i < max && n > 0)
    {
        out[i] = n % 3;
        n /= 3;
        i++;
    }
    return i;
}

ただし n_i, m_i は常に範囲内の [0, 2] (基本3桁なので)。 C(n_i, m_i) は非常に計算しやすい。

// calculate the binomial coefficient for n < 3
unsigned binom_max_2(unsigned n, unsigned k)
{
    if (n < k)
        return 0;
    switch (n)
    {
        case 0:
        case 1:
            return 1;
        case 2:
            return 1 + (k == 1);

        // shouldn't happen
        default:
            return 0;
    }
}

そして、今度は定理そのものです。

// Lucas's theorem for p = 3
unsigned lucas_3(
    unsigned len_n, const unsigned * dig_n,
    unsigned len_k, const unsigned * dig_k
)
{
    // use modulo product rule:
    // prod[i] % 3 = ((prod[i - 1] % 3) * value[i])      
    unsigned prod = 1;
    for (unsigned i = 0; i < len_n; i++) {
        unsigned n_i = dig_n[i];
        unsigned k_i = (i < len_k) ? dig_k[i] : 0;
        prod = (prod * binom_max_2(n_i, k_i)) % 3;
    }
    return prod % 3;
}

文字変換を行います。

// convert from 012 to RGB
char int_2_char(int i)
{
    switch (i) {
        case 0: return 'R';
        case 1: return 'G';
        case 2: return 'B';

        // shouldn't happen
        default:
            return '\0';
    }
}

// convert from RGB to 012
unsigned char_2_int(char c)
{
    switch (c) {
        case 'R': return 0;
        case 'G': return 1;
        case 'B': return 2;

        // shouldn't happen
        default:
            return 3;
    }
}

最後に、三角形のアルゴリズムです。

// the problem constraints state that n <= 10 ** 5
// max number of base-3 digits
#define MAX_N_LOG_3 11

// main algorithm function
char triangle(const char * input)
{
    unsigned sum = 0;
    const int n = strlen(input);

    // calculate digits of n - 1
    unsigned dig_n[MAX_N_LOG_3];
    unsigned len_n = conv_base_3(n - 1, MAX_N_LOG_3, dig_n);

    for (unsigned km1 = 0; km1 < n; km1++)
    {
        // calculate digits of k - 1
        unsigned dig_k[MAX_N_LOG_3];
        unsigned len_k = conv_base_3(km1, MAX_N_LOG_3, dig_k);

        // calculate C(n - 1, k - 1) mod 3
        unsigned Cnk_mod3 = lucas_3(len_n, dig_n, len_k, dig_k);

        // add using the modulo rule
        sum = (sum + Cnk_mod3 * char_2_int(input[km1])) % 3;
    }

    // value of (-1) ** (n - 1)
    // (no need for pow; just need to know if n is odd or even)
    int sign = (n % 2) * 2 - 1;

    // for negative numbers, must resolve the difference
    // between C's % operator and mathematical mod
    int sum_mod3 = (3 + (sign * (int)(sum % 3)) % 3;
    return int_2_char(sum_mod3);
}

上記のコードはすべてのテストに合格しています。パフォーマンスではなく、わかりやすさを優先して書かれていることに注意してください。

では、なぜこのコードは割り当てられた時間内にすべてのテストに合格することができたのでしょうか。一方、単純なテーブルベースのアプローチでは合格できなかったのです。それは、その 時間の複雑さ :

• テーブルベースのアプローチでは、三角形のすべてのレベルを処理するため、次のようになります。 O(n^2) (参照 三角形の数字 ).

• もちろん、ルーカスのアルゴリズムを使えば、トップレベルのみを処理すればよいのですが、アルゴリズム自体は O(log n) のすべての桁をループするので n (基数は関係なく)です。全体の複雑さは O(n log n) それでも大幅な改善です。