[解決済み】2次元の点がポリゴン内にあるかどうかを判断するにはどうしたらいいですか？

質問

を作成しようとしています。 速い 2Dポイントインサイドポリゴンアルゴリズム。 Polygon.contains(p:Point) ). 効果的なテクニックの提案をお願いします。

解決方法は？

グラフィックの場合、むしろ整数の方が好ましくないですね。多くのシステムはUIペイントに整数を使いますが（結局ピクセルはint）、たとえばmacOSはすべてにfloatを使います。macOSはポイントしか知らないので、ポイントは1ピクセルに変換できますが、モニターの解像度によっては別のものに変換されるかもしれません。Retinaスクリーンでは、半分のポイント（0.5/0.5）がピクセルになります。それでも、macOSのUIが他のUIに比べて著しく遅いということには気づかなかった。結局のところ、3D API (OpenGL または Direct3D) も float で動作し、最新のグラフィック ライブラリは GPU アクセラレーションを利用することが非常に多いのです。

今、スピードが一番の関心事とおっしゃいましたが、よし、スピードを追求しましょう。高度なアルゴリズムを実行する前に、まず簡単なテストをしてみましょう。まず 軸合わせされたバウンディングボックス ポリゴンの周りに これは非常に簡単で速く、すでに多くの計算を節約することができます。 どのように動作するのでしょうか？ポリゴンのすべての点を反復処理し、XとYの最小値/最大値を求めます。

例えば、次のような点があるとします。 (9/1), (4/3), (2/7), (8/2), (3/6) . これは、Xmin が 2、Xmax が 9、Ymin が 1、Ymax が 7 であることを意味します。 2 つの辺 (2/1) と (9/7) を持つ長方形の外側の点は、ポリゴン内に存在することはできません。

// p is your point, p.x is the x coord, p.y is the y coord
if (p.x < Xmin || p.x > Xmax || p.y < Ymin || p.y > Ymax) {
    // Definitely not within the polygon!
}

これは、どの点に対しても最初に実行されるテストです。見ての通り、このテストは超高速ですが、非常に粗いものでもあります。境界矩形内にある点を処理するためには、より洗練されたアルゴリズムが必要です。これを計算する方法はいくつかあります。どの方法が有効かは、ポリゴンが穴を持つか、常にソリッドであるかに依存します。以下は立体の例である（凸と凹）。

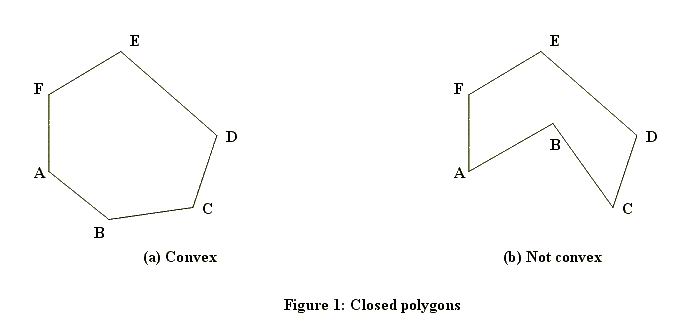
そして、こちらは穴の開いたもの。

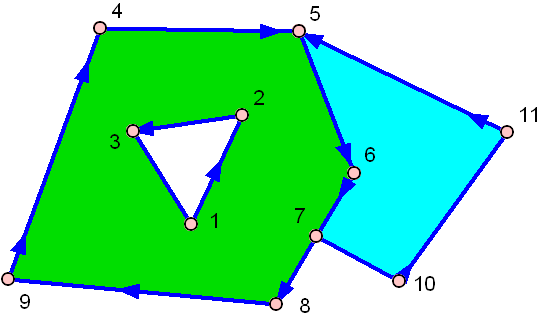
緑色のものは、真ん中に穴が開いているのです

上記の3つのケースをすべて処理でき、なおかつかなり高速な最も簡単なアルゴリズムは、次のように名付けられました。 レイキャスティング . このアルゴリズムの考え方はとてもシンプルです。ポリゴンの外側の任意の場所から自分のポイントまで仮想光線を引き、それがポリゴンの辺に当たる回数を数えます。ヒットした回数が偶数ならポリゴンの外側、奇数なら内側です。

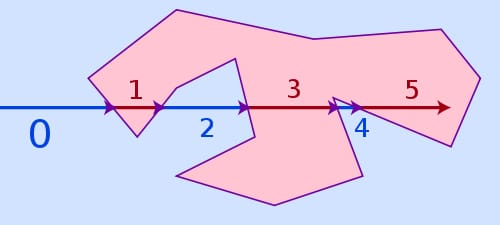
は 巻数アルゴリズム これはポリゴンラインに非常に近い点に対してより正確ですが、速度もかなり遅くなります。ポリゴンの辺に近すぎる点は、浮動小数点数の精度と丸めの問題でレイキャストに失敗するかもしれませんが、実際にはほとんど問題にはなりません。

上のバウンディングボックスはまだあるでしょ？バウンディングボックスの外側にある点を選んで、それをレイの始点にすればいいのです。例えば、点 (Xmin - e/p.y) は確実にポリゴンの外側です。

しかし e ? まあね。 e (実際にはイプシロン) はバウンディングボックスにいくつかの パディング . 先ほど言ったように、レイトレーシングはポリゴンの線に近づきすぎると失敗します。バウンディングボックスはポリゴンと等しいかもしれないので（ポリゴンが軸合わせされた矩形であれば、バウンディングボックスはポリゴンそのものと等しい！）、これを安全にするためにいくつかのパディングが必要だ、それだけである。どの程度の大きさを選べばよいのでしょうか e ? あまり大きくしないでください。描画に使用する座標系の縮尺に依存します。ピクセルステップ幅が1.0なら、1.0を選べばいい（0.1でもいいんだけどね）。

レイの始点と終点の座標がわかったので、問題は「quot」から「quot」に移ります。 はポリゴン内の点 から「" ポリゴンの辺と交差するレイの頻度 "です。したがって、以前のようにポリゴンの点を扱うだけではだめで、今度は実際の辺が必要です。辺は常に2つの点によって定義されます。

side 1: (X1/Y1)-(X2/Y2)
side 2: (X2/Y2)-(X3/Y3)
side 3: (X3/Y3)-(X4/Y4)
:

レイをすべての側面に対してテストする必要があります。レイをベクトル、各辺をベクトルと考えます。光線は各辺に一度だけ当たるか、全く当たらないかでなければなりません。同じ辺に2回当たることはありません。2次元空間の2本の線は、平行でない限り、必ず一度だけ交差します（この場合、交差することはありません）。しかし、ベクトルの長さには限りがあるので、2つのベクトルは平行でなくても、短すぎて決して交わることはないでしょう。

// Test the ray against all sides
int intersections = 0;
for (side = 0; side < numberOfSides; side++) {
    // Test if current side intersects with ray.
    // If yes, intersections++;
}
if ((intersections & 1) == 1) {
    // Inside of polygon
} else {
    // Outside of polygon
}

ここまではいいとして、2つのベクトルが交差しているかどうかをテストするにはどうしたらいいのでしょうか？ここにC言語のコードがあります（テストはしていません）ので、これでうまくいくはずです。

#define NO 0
#define YES 1
#define COLLINEAR 2

int areIntersecting(
    float v1x1, float v1y1, float v1x2, float v1y2,
    float v2x1, float v2y1, float v2x2, float v2y2
) {
    float d1, d2;
    float a1, a2, b1, b2, c1, c2;

    // Convert vector 1 to a line (line 1) of infinite length.
    // We want the line in linear equation standard form: A*x + B*y + C = 0
    // See: http://en.wikipedia.org/wiki/Linear_equation
    a1 = v1y2 - v1y1;
    b1 = v1x1 - v1x2;
    c1 = (v1x2 * v1y1) - (v1x1 * v1y2);

    // Every point (x,y), that solves the equation above, is on the line,
    // every point that does not solve it, is not. The equation will have a
    // positive result if it is on one side of the line and a negative one 
    // if is on the other side of it. We insert (x1,y1) and (x2,y2) of vector
    // 2 into the equation above.
    d1 = (a1 * v2x1) + (b1 * v2y1) + c1;
    d2 = (a1 * v2x2) + (b1 * v2y2) + c1;

    // If d1 and d2 both have the same sign, they are both on the same side
    // of our line 1 and in that case no intersection is possible. Careful, 
    // 0 is a special case, that's why we don't test ">=" and "<=", 
    // but "<" and ">".
    if (d1 > 0 && d2 > 0) return NO;
    if (d1 < 0 && d2 < 0) return NO;

    // The fact that vector 2 intersected the infinite line 1 above doesn't 
    // mean it also intersects the vector 1. Vector 1 is only a subset of that
    // infinite line 1, so it may have intersected that line before the vector
    // started or after it ended. To know for sure, we have to repeat the
    // the same test the other way round. We start by calculating the 
    // infinite line 2 in linear equation standard form.
    a2 = v2y2 - v2y1;
    b2 = v2x1 - v2x2;
    c2 = (v2x2 * v2y1) - (v2x1 * v2y2);

    // Calculate d1 and d2 again, this time using points of vector 1.
    d1 = (a2 * v1x1) + (b2 * v1y1) + c2;
    d2 = (a2 * v1x2) + (b2 * v1y2) + c2;

    // Again, if both have the same sign (and neither one is 0),
    // no intersection is possible.
    if (d1 > 0 && d2 > 0) return NO;
    if (d1 < 0 && d2 < 0) return NO;

    // If we get here, only two possibilities are left. Either the two
    // vectors intersect in exactly one point or they are collinear, which
    // means they intersect in any number of points from zero to infinite.
    if ((a1 * b2) - (a2 * b1) == 0.0f) return COLLINEAR;

    // If they are not collinear, they must intersect in exactly one point.
    return YES;
}

入力値は 2つのエンドポイント のベクトル1( v1x1/v1y1 と v1x2/v1y2 )とベクトル2( v2x1/v2y1 と v2x2/v2y2 ). つまり、2つのベクトル、4つの点、8つの座標があるわけです。 YES と NO はクリアです。 YES は交差点を増やします。 NO は何もしません。

COLLINEARはどうでしょうか？両方のベクトルが同じ無限直線上にあることを意味します。位置と長さによって、全く交差しないか、無限の点で交差することになります。このケースをどう扱うかは絶対的なものではなく、私ならどちらにしても交点としてカウントしない。まあ、浮動小数点数の丸め誤差があるので、このケースは実際にはかなり稀です。 == 0.0f の代わりに、次のようなものがあります。 < epsilon ここで、εはかなり小さな数字です。

より多くの点をテストする必要がある場合、多角形の辺の線形方程式標準形をメモリに保持し、これらを毎回再計算する必要がないようにすれば、確かに全体を少し高速化することができます。これは、ポリゴンの辺ごとに3つの浮動小数点値をメモリに保存する代わりに、テストのたびに2つの浮動小数点数の乗算と3つの浮動小数点数の減算を節約することができます。これは、典型的なメモリと計算時間のトレードオフです。

最後になりますが、いかがでしょうか。もし、3Dハードウェアを使って問題を解決する可能性があるなら、面白い選択肢があります。GPUにすべての仕事をさせればいいのです。画面外に絵の具を塗る面を作ります。それを完全に黒で塗りつぶします。次に、OpenGLまたはDirect3Dに、あなたのポリゴン（あるいは、点がどれかのポリゴンの中にあるかどうかをテストしたいだけで、どのポリゴンにあるかは気にしない場合は、すべてのポリゴン）を描かせ、ポリゴンを別の色、例えば白で塗りつぶします。ある点がポリゴン内にあるかどうかを調べるには、描画面からその点の色を取得します。これは単なる O(1) メモリフェッチである。

もちろんこの方法は、描画面が巨大である必要がない場合にのみ使用可能です。GPU のメモリに収まらない場合、この方法は CPU で行うより遅くなります。もし描画面が巨大になる必要があり、GPU が最新のシェーダをサポートしているなら、上に示したレイキャスティングを GPU シェーダとして実装すれば GPU を使うことができますし、もちろんそれは可能です。ポリゴン数が多い場合や、テストするポイントの数が多い場合は、この方法が有効で、いくつかのGPUは64から256のポイントを並行してテストすることができると考えてください。しかし、CPU から GPU へのデータ転送には常にコストがかかるので、2、3 の単純なポリゴンに対して 2、3 のポイントをテストするだけなら、ポイントまたはポリゴンが動的で頻繁に変更される場合、GPU アプローチはほとんど利益を上げないことに注意 してください。