第1章 ニューラルネットを用いた手書き数字の認識

人間の視覚システムは、世界でも不思議な存在です。次のような手書きの数字の列を考えてみましょう。

<センター

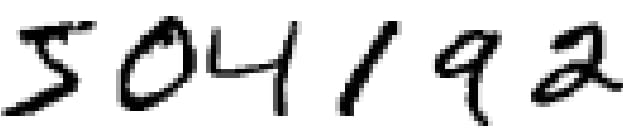
多くの人は、この数字が504192であることを容易に認識する。その容易さは欺瞞に満ちている。人間は、脳の各半球に一次視覚野（V1）を持っており、そこには1億4千万個の神経細胞と、その間にある数百億個の神経接続が存在する。しかし、人間の視覚には、V1だけでなく、V2、V3、V4、V5という一連の視覚野があり、段階的により複雑な画像処理を行っているのです。私たちは、何億年もの進化によって調整され、視覚世界を理解するために見事に適応したスーパーコンピューターを頭の中に搭載しているのです。手書きの数字を認識するのは簡単なことではありません。むしろ、私たち人間は、目で見たものを理解するのが驚くほど得意なのです。そのため、私たちは通常、視覚システムがいかに難しい問題を解決しているかを理解していません。

視覚的なパターン認識の難しさは、上のような数字を認識するプログラムをコンピュータに書こうとするとよくわかる。9は上部に輪っかがあり、右下に縦線がある」というような、図形を認識する際の単純な直感は、アルゴリズムで表現するにはそれほど単純ではないことがわかる。このようなルールを正確に作ろうとすると、例外や注意点、特殊なケースなど、すぐに迷宮入りしてしまうのです。

ニューラルネットワークは、この問題に別の方法でアプローチしています。それは、学習例と呼ばれる手書きの数字を大量に取り込むというものです。

<センター

つまり、ニューラルネットワークは、例文から手書きの数字を認識するためのルールを自動的に推論しているのだ。さらに、学習例の数を増やすことで、ネットワークは手書き文字についてより多くを学ぶことができます。ですから、上記では100桁の学習例を示しましたが、おそらく数千、あるいは数百万、数十億の学習例を使用すれば、より優れた手書き文字認識装置を構築することができるでしょう。

この章では、手書きの数字を認識することを学習するニューラルネットワークを実装したコンピュータプログラムを書きます。さらに、この後の章では、精度を99％以上に向上させるためのアイデアを紹介します。実際、市販されている最高のニューラルネットワークは、現在、銀行が小切手を処理したり、郵便局が住所を認識したりするのに使われているほどです。

私たちが手書き文字認識に注目しているのは、ニューラルネットワーク全般について学ぶための優れたプロトタイプ問題だからです。手書きの数字を認識するのは並大抵のことではありませんが、非常に複雑な技術を必要とするほど難しくなく、ディープラーニングなどのより高度な技術を開発するには最適なプロトタイプなのです。本書の後半では、これらのアイデアをコンピュータビジョンの他の問題や、音声、自然言語処理、その他の領域の問題にどのように適用できるかを説明します。

もちろん、この章のポイントが手書きの数字を認識するコンピュータ・プログラムを書くことだけであれば、この章はもっと短くなるはずです。この章では、2種類の重要な人工ニューロン（パーセプトロンとシグモイド・ニューロン）や、確率勾配降下法と呼ばれるニューラルネットワークの標準学習アルゴリズムなど、ニューラルネットワークに関する多くの重要なアイデアを展開することになります。ここでは、特に  なぜ  そのため、この章の終わりには、ディープラーニングとは何かを理解することができるようになりますが、その分、より深い理解を得ることができます。この章の終わりには、深層学習とは何か、そしてなぜそれが重要なのかを理解できるようになるでしょう。

パーセプトロン

ニューラルネットワークとは？まず始めに、人工ニューロンの一種である「ニューラルネットワーク」について説明します。  パーセプトロン . パーセプトロンは  開発された  1950年代から1960年代にかけて、科学者である  フランク・ローゼンブラット に触発され  作品  によって  ウォーレン・マッカロク  と  ウォルター・ピッツ . 今日、人工ニューロンの他のモデルを使用することがより一般的になっています。本書、そしてニューラルネットワークに関する最近の研究の多くでは、主なニューロンモデルとして  シグモイド・ニューロン . シグモイド・ニューロンについては、まもなく紹介する。しかし、なぜシグモイドニューロンがこのように定義されているのかを理解するためには、まずパーセプトロンについて理解する時間を取る価値があります。

では、パーセプトロンの仕組みはどうなっているのでしょうか。パーセプトロンは、いくつかの2進数の入力を受け取ります。  <スパン <スパン <スパン x 1 <スパン , <スパン x 2 <スパン , ... x 1 , x 2 , ... であり、1つのバイナリ出力を生成する。

<センター この例では、パーセプトロンは3つの入力を持ちます。  <スパン <スパン <スパン <スパン <スパン <スパン <スパン x 1 <スパン , <スパン x 2 <スパン , <スパン x 3 <スパン x 1 , x 2 , x 3 . 一般に、入力は多くても少なくてもよい。ローゼンブラットは、出力を計算するための簡単なルールを提案した。と紹介されました。  <ウェイト 重さ ,  w 1 , w 2 , ... w 1 , w 2 , ... は、それぞれの入力が出力に与える重要度を表す実数である。  0 0  または  1 1 は、加重和があるかどうかで決まります。  ∑ j w j x j ∑ j w j x j  は、ある値より小さいか大きい  閾値 . 重みと同様に、閾値も実数であり、ニューロンのパラメータとなる。より正確な代数的用語で言えば