Yolov3のベゼル予測について、これまでで最も詳細な分析を行いました。

更新：この記事の最新版はZhihuで更新されました、csdnの記事はロジックがめちゃくちゃな古いバージョンです、リンク先をご覧ください。 <スパン Yolo検出フレーム予測の超詳細解析 - Zhihu 我々は、すべての国境予測の式を知っているyolov3紙を読んで、しかし、それは著者がそうしたい理由を正確に理解することは困難である、ここで私は私の個人的な洞察を要約して説明するために提供する、疑問を学ぶときに発生するのは簡単の文字列をまとめ、あなたを助けるために楽しみにしています。1、ネットワーク入力ボリューム分析は、まずネットワークにする必要があります... https://zhuanlan.zhihu.com/p/49995236

---

我々は、yolov3論文を読んでボーダー予測式を知っている、しかし、それは著者がそうしたい理由を正確に理解することは困難である、ここで私は私の個人的な洞察を要約して説明するために提供し、混乱に遭遇することを学ぶのは簡単の文字列をまとめて、あなたを助けるために楽しみにして、間違った場所を理解すると、私を批判して修正してください、私はちょうど少し白ああ、あなたともっと通信するためにも発行、私は正しいかどうかはわからないの理解を参照してください。

論文中のボーダー予測式は以下の通りです。

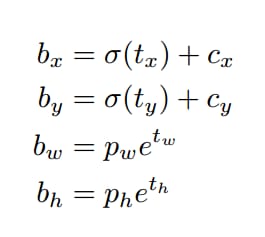
yolov3では、特徴マップの各グリッドセルの幅と高さは1である。下の図1の場合、このbbox bounding boxの中心は2行2列目のグリッドセルに属し、その左上隅座標は（1,1）なので、Cx=1,Cy=1である。式中のPwとPhは、特徴マップにマッピングされた定義済みアンカーボックスの幅と高さである( アンカーボックスはもともとyolov3.cfgに書かれている416*416座標系に対する相対座標で設定されており、コードはcfgから読み込んだ座標をストライドを32で割ってフィーチャーマップ座標系にマッピングしています。 ).

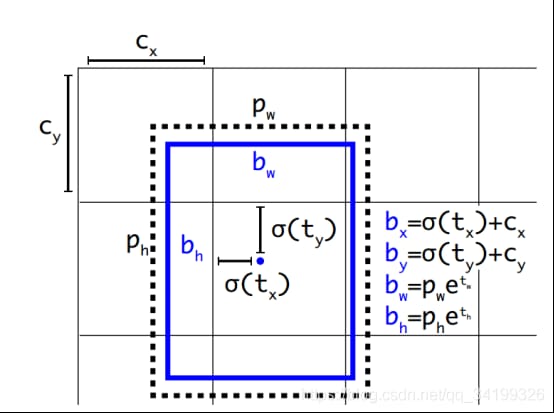
                                                          図1

       最終的に得られた境界座標値はbx,by,bw,bh、すなわち特徴マップに対するバウンディングボックスbboxの位置と大きさで、これが我々が必要とする予測出力座標である。 しかし、このネットワークの学習目標は、実際には4つのオフセット tx,ty,tw,th です。 ここで tx,ty は予測された座標のオフセットで tw,th はスケールのスケーリングである。この4つのオフセットがあれば、先の式により本当に必要なbx,by,bw,bhの4つの座標が自然に求まります。では、なぜbx,by,bw,bhを直接学習しないのか？YOLOの出力は畳み込み特徴マップであり、特徴マップの深さに沿ったバウンディングボックス属性を含んでいるからです。バウンディングボックス属性は、セルを重ねたときの予測値から導かれる。したがって、もし (5,6) にあるそのセルの2番目のバウンディングボックス bbox にアクセスする必要があれば、map[5,6, (5+C): 2*(5+C)] でインデックスを作る必要がある。この形式は出力処理（目標信頼度による閾値、中心へのグリッドオフセットの追加、アンカーポイントの適用など）には不便なので、オフセットを求めるだけにしている。そうすると、この方法ではオフセットを求めるだけでよく、どうせ等価である bx,by,bw,bh を上記の式で求めることも可能である。また、オフセットを学習することで、元々与えられているネットワークのアンカーボックス座標を線形回帰で微調整（平行移動＋拡大縮小）していくことで徐々に真実に近づけていくことも可能です。

なお、入力サイズは416×416ですが、元画像はどちらの面でも416×416に拡大縮小されていることに注意してください。 長辺が目的の入力サイズ416に、短辺が歪みなくスケーリングされるように、スケールmin(w/img_w, h/img_h)を取る。 図2に示すように、スケーリングされた寸法はnew_w, new_h=416,312で、必要な入力サイズはw,h=416*416となる。

                                                                図2

残りのグレーの部分は(128,128,128)で埋められ、416*416を構成します。これはトレーニング、テストともに元のグラフを操作するために必要です。pytorchのコードはこれを理解するのに優れています。以下の関数は、元のグラフの変換を実装しています。

def letterbox_image(img, inp_dim):
    """
    lteerbox_image() scales the image to the aspect ratio, fills the empty space with (128,128,128), and resizes the image
    Specifically, at this point, one side is exactly equal to the target length, and the other side is less than or equal to the target length
    Copy the scaled data to the center of the canvas, and return to finish scaling
    """
    img_w, img_h = img.shape[1], img.shape[0]
    w, h = inp_dim # inp_dim is the size that needs to be resized (e.g. 416*416)
    # take min(w/img_w, h/img_h) this ratio to scale, scaling the size of new_w, new_h, that is, to ensure that the longer side scaled exactly equal to the target length (the required size), the other side of the size after scaling has not been filled.
    new_w = int(img_w * min(w/img_w, h/img_h))
    new_h = int(img_h * min(w/img_w, h/img_h))
    resized_image = cv2.resize(img, (new_w,new_h), interpolation = cv2.INTER_CUBIC) # scale the image to new_w x new_h by constant aspect ratio, 768 x 576 image scaled to 416x312., using double triple interpolation
    # Create a canvas, copy the resized_image data to the center of the canvas.
    canvas = np.full((inp_dim[1], inp_dim[0], 3), 128) # generate an array of the final image size we need hxwx3, here we generate an array of 416x416x3, with each element valued at 128
    # assign the part of the array corresponding to new_wxnew_hx3 (the centers of these two parts should be aligned) to the array just obtained by scaling the original image, to get the final scaled image
    canvas[(h-new_h)//2:(h-new_h)//2 + new_h,(w-new_w)//2:(w-new_w)//2 + new_w, :] = resized_image
    
    return canvas

そして、次のことに注意しましょう。 yolov3が学習データに必要とするラベルは、元の画像サイズに正規化されています。これは、大きな縁取りの影響が小さな縁取りの影響よりも大きいために行われるものです これは、大枠の影響が小枠の影響より大きいため、大枠も小枠も同等に扱い、学習が収束しやすいように正規化したものである。ラベルは元の図の大きさに応じて正規化されているので、自分でデータセットを作る際には正規化する必要があり、yolov3が必要とするラベルに変換する方法についてはネット上に多くのチュートリアルがあります。 インスタンスのセグメンテーションデータセットをターゲット検出用データセットに変換する_プログレッシブ王のブログ - CSDNブログ_セグメンテーションデータセットをyoloに変換する方法 は、ここでは繰り返さない。

        アンカーボックスについて説明します。YOLO3は、FPN予測特徴マップ（13*13,26*26,52*52）ごとに3つのアンカーボックスを設定し、様々な大きさの合計9つのアンカーボックスをクラスタリングしています。(30x61), (62x45), (59x119), (116x90), (156x198), (373x326)である。最小の13*13特徴量マップでは、知覚野が最大であるため、最大のアンカーボックス（116x90）、（156x198）、（373x326）を適用し（これらの座標は416*416のもので、もちろん、13*13に縮小するには32で割らなければならない）、大きなターゲットを検出することに適している。中位の26*26の特徴マップは、知覚野が中位であるため中位のターゲットを検出するのに適しており、中位のアンカーボックス（30x61）、（62x45）、（59x119）が適用される。52*52の大きな特徴マップは、受容野が小さいので、小さなターゲットの検出に適した最小のアンカーボックス（10x13）、（16x30）、（33x23）が適用される。Faster-Rcnnと同様に、特徴マップの各画素（つまり各グリッド）には3つの対応するアンカーボックスがあり、例えば13*13特徴マップの各グリッドには3つのアンカーボックス (116x90), (156x198), (373x326) があります（これらの座標は32スケーリングサイズで割る必要があるのです）。

では、4つの座標tx,ty,tw,thはどのようにして求められるのでしょうか？学習用サンプルの場合、多くの論文では、この4つの座標を求めるために、真実のフレームであるグランドトゥルースを使用する必要があります。

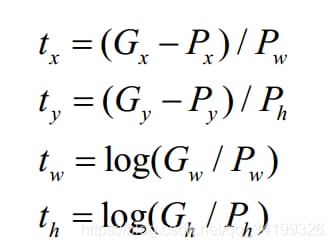
上の式は、faster-rcnnシリーズで使用されている式です。fast-rcnn シリーズの Px,Py は、あらかじめ設定されているアンカーボックスの中心点座標である。Pw と Ph は、特徴地図上のアンカーボックスの幅と高さである。Gx、Gy、Gw、Ghは当然4つの座標のこの特徴マップのグランドトゥルースです（実際には、上記は、プロセスを説明している、最初に416 * 312などの小領域の下に416 * 416座標の元の地図のアスペクト比一定のマッピングによると、min（w/img_w、h/img_h）を取る この比が416 * 312に拡大し、416 * 416、座標変換だけy1下416 * 312で真実を聞かせて必要記入します。 y2（つまり、左上と右下の垂直座標）プラス図2の灰色の部分の半分、y1 = y1 +（416-416/768*576）/2 = y1 +（416-312）/2, y2同じ操作、x1の座標系の変換。 x2,y1,y2は、座標系（416*312）の実際の赤いボックスから416*416の下に、bboxが歪まないようにし、その後ストライドで割って特徴マップに対する相対座標を取得します）。

アンカーボックスのx,y座標からオフセットを引くとわかりやすい。 なぜフィーチャーマップ上のアンカーボックスの幅と高さで割るのか？ 絶対尺を相対尺に変えることでしょうね、やはりオフセットとして、あまり大きくはできないですよね？また、アンカーボックスのスケールによってGx-Pxを使い分けるのは明らかにおかしいですし、アンカーボックスには大きいものもあれば小さいものもあります。

       しかし、yolov3では、faster-rcnnシリーズで使われている方程式が最初の2行で異なっています。yolov3 では、Px,Py の代わりに、特徴地図上のグリッドセルの左上隅の Cx,Cy 、つまり Gx,Gy から Cx,Cy を引いたものが使われています。 x,y座標はアンコンボックスに対してオフセットされていないため、Pw,Phで割る必要はない。

つまり、tx = Gx - Cxです。

                  ty = Gy - Cy

これは、グリッドセルの左上隅の座標から、bboxの中心のオフセットを直接求めるものです。

tw と th yolov3 の計算式は、Faster-RCNN シリーズと同じで、オブジェクトがあるバウンディングボックスの長さと幅、アンカーボックスの長さと幅の比率で、Faster-RCNN でも YOLO でも、バウンディングボックスの長さと幅を直接回帰させるのではなく 学習によって不安定な勾配がもたらされることを懸念して、スケールは対数空間にスケーリングされている . なぜなら、変換を行わず、相対変形量twを直接予測する場合、ボックスの幅と高さが負になることはありえないので、tw>0が必要になるからです。このように、SGDでは直接できない、不等式条件制約のある最適化問題をやっていることになります。ですから、まず対数変換を行い、その不等式制約を取り除けば、問題ありません。

ここで重要な問題があります。スケールフィーチャーマップには3つのアンカーがありますが、あるグランドトゥルースボックスに対して、どのアンカーがマッチングを担当するのでしょうか？YOLOv1と同様に、学習画像中のグランドトゥルースに対して、そのセントロイドがセル内にある場合、そのセル内の3つのアンカーボックスが予測する役割を担っています。 つまり、グランドトゥルースに対して最大のIOUを持つアンカーボックスがそれを予測し、残りの2つのアンカーボックスはグランドトゥルースにマッチしない、というように、予測するアンカーボックスを学習中に正確に決定する必要があります。 YOLOv3では、各セルに最大1つの地上真理が含まれていると仮定する必要があり、実際には基本的に1つ以上はありません。地上真理と一致するアンカーボックスは、座標誤差、信頼誤差（目標値は1）、分類誤差を計算し、その他のアンカーボックスは信頼誤差（目標値は0）のみを計算します。

アンカーボックスは平行移動(tx,ty)と拡大縮小(tw,th)により、グランドトゥルースに合うように微調整が可能である。図3では、赤いボックスがアンカーボックス、緑のボックスがグランドトゥルースで、トランスレーションとスケーリングにより、赤い実線のボックスを赤い破線のボックスまでパンし、緑のボックスまでスケーリングすることができます。 ボーダーの戻りは、パンとスケーリングで微調整するのが一番シンプルな考え方です。

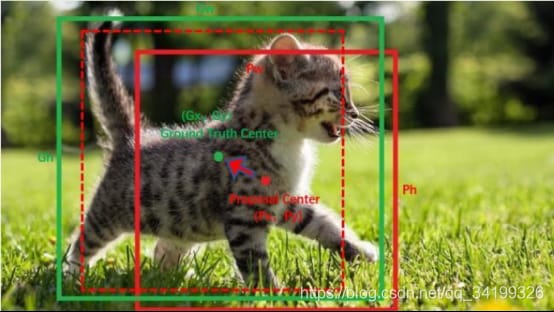
                                                                                図3

なぜボーダーリグレッションは微調整しかできないのか？入力ProposalとGround Truthの差が小さい場合、つまりIOUが大きい場合（RCNNはIoU>0.6に設定）、変換は 一次変換 次に そして、線形回帰を使うことができます (線形回帰とは、入力固有ベクトルXが与えられたとき、線形回帰後の値が真値Y（Ground Truth）に非常に近くなるように、パラメータWのセットを学習することである）。すなわち、Y≈WX ) 窓の微調整をモデル化するために そうでなければ、学習した回帰モデルは機能しません（ProposalがGTから遠い場合、複雑な非線形問題となり、線形回帰でモデル化するのは明らかに合理的ではありません）。

その後、tx,ty,tw,thを得るために差と比を行うために訓練で使用groundtruthの4座標は、テストは予測bboxが良いですが、式を変更するには簡単です、GxとGyは予測X、Y、Gw、Ghは予測W、Hにすることができますに変更してください。

ネットワークは学習を続けることができる tx,ty,tw,thのオフセットと予測時のスケールのスケーリング この4つのオフセットを使ってbx,by,bw,bhを求めれば十分で、次に問題なのは

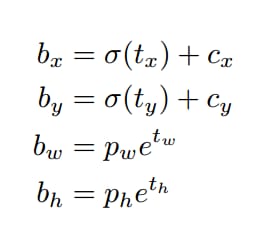
この式tx,tyはなぜシグモイドである必要があるのでしょうか？前述したように、yolov3ではGx - CxをPwで割ってtxを求めるのではなく、Gx - Cxから直接txを求めますが、txが大きくなり、>1.になる可能性が高いという問題があります（Pwで割ってスケールを正規化していないため）。 シグモイドを使用して tx,ty を [0,1] 区間に圧縮することで、ターゲットの中心が予測を行うグリッドセルにあることを効果的に保証し、過度のシフトを防ぎます。 . 例えば、ネットワークはバウンディングボックスの中心の正確な座標を予測するのではなく、予測されたターゲットのグリッドセルの左上隅に関連するオフセットtx,tyを予測することを学んだばかりである。特徴マップにおけるオブジェクトの中心の実際の座標は明らかに(6.4,6.7)である。この状況は問題ないが、tx,ty が 1 より大きい場合、例えば (1.2,0.7) のように、特徴マップにおける物体の中心の実際の座標は (7.2,6.) となる。 7）であり、物体の中心は物体が属するグリッドセルの外側にあるが、（6,6）グリッドセルはこのセルに物体の中心があると検出する（ヨーロはどのグリッドセルに物体全体の中心を取ること）ので矛盾していることに注意してください。(6,6)のグリッドセルの左上隅がオブジェクトの予測を担当しているため、オブジェクトの中心はこのグリッドセルに現れなければならず、その隣のグリッドに現れることはできないため、一旦計算したtx,tyが1より大きくなると矛盾が生じるため、正規化する必要があります。

 式の最後の2行を見てください。なぜtwが指数関数的である必要があるのでしょうか？これは理解できます。tw,thは対数空間に対数スケールでスケーリングされているので、当然指数的に戻す必要があり、これにより0より大きいことが保証されます。左辺にPwまたはPhを乗じることについては、tw=log(Gw/Pw)なので、当然戻し、真の幅と高さを得る必要があります。

特徴マップのサイズをW, Hと書くことで（例：13*13）、画像全体に対するbboxの位置と大きさが計算できる（4つの値すべてが[0,1]の間隔になるように）。 bboxの位置予測を[0,1]に拘束することで、モデルを安定的に学習させやすくなる (0,1]区間でない場合、yoloの各bboxは85次元、最初の5属性は(Cx,Cy,w,h,confidence)、最後の80はカテゴリ確率、座標を正規化しないと、この確率値での学習では収束しません ah)

先に計算したbx,bwをWで、by,bhをHで割ればいいだけです。

box get_yolo_box(float *x, float *biases, int n, int index, int i, int j, int lw, int lh, int w, int h, int stride)
{
    box b;
    b.x = (i + x[index + 0*stride]) / lw;
    // This is equivalent to knowing the index of x, to find the index of y, offset l.w*l.h by an index
    b.y = (j + x[index + 1*stride]) / lh;
    b.w = exp(x[index + 2*stride]) * biases[2*n] / w;
    b.h = exp(x[index + 3*stride]) * biases[2*n+1] / h;
    return b;
}
float delta_yolo_box(box truth, float *x, float *biases, int n, int index, int i, int j, int lw, int lh, int w, int h, float *delta, float scale, int stride)
{
    box pred = get_yolo_box(x, biases, n, index, i, j, lw, lh, w, h, stride);
    float iou = box_iou(pred, truth); 
    float tx = (truth.x*lw - i); 
    float ty = (truth.y*lh - j); 
    float tw = log(truth.w*w / biases[2*n]); 
    float th = log(truth.h*h / biases[2*n + 1]);
    scale = 2 - groundtruth.w * groundtruth.h 
    delta[index + 0*stride] = scale * (tx - x[index + 0*stride]); 
    delta[index + 1*stride] = scale * (tty - x[index + 1*stride]);
    delta[index + 2*stride] = scale * (tw - x[index + 2*stride]);
    delta[index + 3*stride] = scale * (th - x[index + 3*stride]);
    return iou;
}

        上の2つの関数は、yolov3のdarknetフレームワークのsrc/yolo_layer.cのコードからきており、関数パラメータfloat* xは、前の畳み込み層の出力からきています。まず、関数 get_region_box() のパラメータを見ましょう。バイアスはあらかじめ定義されたアンカーボックスの幅と高さを格納し、（lw,lh）はヨーロ層の入力特徴マップの幅と高さ（13*13）、（w,h）はネットワーク全体の入力マップスケール 416*416 を表します。get_yolo_box() 関数は、論文にある式を利用し、特徴マップの幅と高さ、入力マップの幅と高さをそれぞれ使って結果を正規化しており、先ほどの式に相当する（b.w と b.h が 416 で割られているが、これは以下の関数で tw と th に w,h=416 、 x,y に特徴マップサイズを用いているためである）。なお、ここでの truth.x は、学習用ラベルの txt ファイルの元の正規化座標ではなく、補正後の座標である（元の画像のアスペクト比座標系（416*312）からネットワーク入力 416*416 座標系へのラベルの変更だけでなく、データ拡張後のラベルの変更も考慮されている）。 そしてこの仕組みは、非常に遠いターゲットを予測しないように回帰を制限するために、その では、この予測範囲はどのくらいなのでしょうか？(b.x,b.y) の最小値は (i,j) で最大値は (i+1,x+1) であり、すなわちセントロイドは特徴マップ上で最大1ピクセルだけ移動する（入力マップをn倍ダウンサンプリングして特徴マップを得、特徴マップの1ピクセルが入力マップのnピクセルに対応すると仮定） (b.x,b.y) は、入力マップの1ピクセルの移動に対応し、入力マップの1ピクセルの移動に対応している (i,j,x)である。 w,b.h) は最大でも (2.7 * anchor.w, 2.7 * anchor.h) であり，最小値は (anchor.w, anchor.h) で，これは入力マップのサイズにおける値である．2番目の関数 delta_yolo_box は tx,ty,tw,th がどのように得られるかを詳細に示しており、前の文が基本的に正しいことを検証しています。

また、コードの中にscale = 2 - groundtruth.w * groundtruth.h というコメントがありますが、これはどういう意味でしょうか？実は、yolov1 の作者が の損失は、ボーダーの大きさの違いを小さくするために、幅と高さのオープンルートです。 bbox予測の異なるサイズについては、大きなbbox予測偏差よりも小さなbbox予測偏差の同じサイズは、IOUに多くの影響を与えると思うので、平均二乗誤差は、同じ偏差の損失は、ルート記号を取るようにしながら。例えば、100×100のターゲットと10×10のターゲットは、どちらも10ピクセル大きく予測され、予測ボックスは110×110と20×20の比較となります。明らかに最初のケースは受け入れられるが、2番目のケースはバウンディングボックスを1倍大きく予測することに相当するが、ルート関数を使用しない場合、損失は同じだが、ルート記号で幅と高さを増やす場合である。

ルート記号の追加により、10ピクセルという小さなボックスの予測偏差に大きな損失が生じるのは明らかです。また yolov2 と v3 では、単純にルート記号を追加するだけでなく、scale = 2 - groundtruth.w * groundtruth.h で小さなフレームに対する損失を大きくすることで損失関数を改善しました。 .

　　この4つの値に入力ネットワーク画像の幅と高さ（例えば416*416）を掛け合わせると、座標系に対するbboxの位置と大きさ（416*416）が得られます。しかし、入力ネットワーク画像（416x416）に対するborderプロパティを、元の画像を同じ縦横比（416*312）に従ってスケーリングした後の領域の座標に変換することもできます。 ボックスの座標は、元画像を含む塗りつぶし画像の領域に対して計算されるように変換する必要があります。

以下のpytorchのコードをご覧ください。このコードでは scaling_factor = torch.min(416/im_dim_list,1)[0].view(-1,1) すなわち 416/longest edge で scaling_factor をスケーリング比として得ています。

#scaling_factor*img_w and scaling_factor*img_h are the image scaled by the same aspect ratio, i.e. the original image is 768x576 scaled to 416*372 by the same aspect ratio on the longest side.
#After the coordinate conversion, the coordinates are still the absolute coordinates of the image in the input network (416x416) coordinate system, but they are already relative to the coordinates of the 416*372 area, and no longer relative to the (0,0) origin.
output[:,[1,3]] -= (inp_dim - scaling_factor*im_dim_list[:,0].view(-1,1))/2#x1=x1-(416-scaling_factor*img_w)/2 ,x2=x2-(416-scaling_factor*img_w)/2
output[:,[2,4]] -= (inp_dim - scaling_factor*im_dim_list[:,1].view(-1,1))/2#y1=y1-(416-scaling_factor*img_h)/2,y2=y2-(416 -scaling_factor*img_h)/2

実際には、このコードは、図2のグレー部分からy1,y2を半分ずつ引いて、y1=y1-(416-416/768*576)/2=y1-(416-312)/2として、x1,x2,y1,y2の座標系を実際の赤いボックス用の座標系（416*312）へ変換することを意味しているのだそうです。これによって、bboxが歪まないようにし

これは、作者のdarknet用cソースコードsrc/yolo_layer.cでも同様に処理されます。

void correct_yolo_boxes(section *dets, int n, int w, int h, int netw, int neth, int relative)
{
    int i;
	// where new_w is the width of the input image in the letter_box of the network input size after compression, and new_h is the height in the letter_box,
	// Take 1280*720 input image as an example, in the process of letter_box, the width of the original image after resize is 416, then the corresponding height after resize is 720*416/1280,
	// so the height is 234, and the empty part above and below the 234 is filled with 128 before it is used as network input, new_h=234
    int new_w=0;
    int new_h=0;
	// If w>h means that the resize is based on the width/image width as the resize ratio, first get the width of the middle figure, and then get the height according to the ratio
    if (((float)netw/w) < ((float)neth/h)) {
        new_w = netw;
        new_h = (h * netw)/w;
    } else {
        new_h = neth;
        new_w = (w * neth)/h;
    }
    for (i = 0; i < n; ++i){
        box b = dets[i].bbox;
		// The formula here is hard to understand or follow the example above, existing new_w=416,new_h=234, because the resize is compressed with w as the long side
		// so the ratio of x to width remains the same, while b.y represents the ratio of y to image height, before this step of the transformation, b.y represents
		// is the ratio of the y coordinate of the prediction box relative to the height of the network, and to transform it to the ratio relative to the height of the image in the letter_box, it is necessary to first
		// calculate the relative coordinates of y in the letter_box, i.e. (b.y - (neth - new_h)/2./neth), and then divide by the ratio
        b.x = (b.x - (netw - new_w)/2./netw) / ((float)new_w/netw); 
        b.y = (b.y - (neth - new_h)/2./neth) / ((float)new_h/neth); 
        b.w *= (float)netw/new_w;
        b.h *= (float)neth/new_h;
        if(!relative){
            b.x *= w;
            b.w *= w;
            b.y *= h;
            b.h *= h;
        }
        dets[i].bbox = b;
    }
}

座標が得られたので、scaling_factorで割って、真のテスト画像サイズでのbboxの実際の座標にスケーリングすれば完了です。　　

!!!まとめると、元のネットワークで特徴マップが学習した位置情報は、オフセット tx,ty,tw,th であることを知ることができ、これは最終的なフェッチャーマップである Yolo 検出層で、次元（batch_size, num_anchors*bbox_attrs, grid_size , grid_size）、各マップはcocoの80クラスに対して、bbox_attrsは80+5，5で、ネットワークで学習したパラメータtx, ty, tw, thと目標スコアがあるかどうかを示している。また、3つの予測層について、最深層は255*13*13、255はチャンネル、物理的意味はbbox_attrs×3、3はアンカー数であることを特徴としている。損失を計算するために、出力特徴マップは（batch_size, grid_size*grid_size*num_anchors, 5+number of categories）のテンソルに変換する必要があり、ここで5は既に先に精緻化した境界予測式による変換完了結果、すなわちbx,by,bw,bhである。416画像は、3つの検出層による検出後、[(52*52)+(26*26)+(13*13)]*3=10647予測ボックスがあり、その後、x1、y1、x2、y2に変換してイウをカウントし、スコアでフィルタリングしてredundantボックスのほとんどを除去するためにnmsを実行し、損失を計算するなど今操作しますすることができます。

最後に豆知識。確信度とは何か、Pr(Object) ∗ IOU(pred&groundtruth) の説明です。

グリッドセルにオブジェクトがない場合はPr(Object)=0、それ以外はPr(Object)=1、この時点の信頼度は=? 予測されたbboxとground truthのIOU値が信頼度として使われる。したがって、この確信度は、グリッドセルがオブジェクトを含むかどうかを反映するだけでなく、このbbox座標の予測がどの程度正確であるかを予測するものである。予測フェーズでは、カテゴリの確率は、カテゴリ条件付き確率と信頼度を掛け合わせたものとなる。

Pr(Classi|Object) ∗ Pr(Object) ∗ IOU(pred&groundtruth) = Pr(Classi) ∗ IOU(pred&groundtruth)

これにより、各bbox固有のクラスに対するスコアが得られ、その積には、bboxに予測されたクラスが含まれる確率と、bboxにターゲットが含まれるかどうかの精度とbbox座標の両方が含まれます。

このブログはいくつかの良質なブログを参考にしていますが、どこから見たのか思い出せませんので、ここでお礼を申し上げるとともに、このブログでもお世話になることを楽しみにしています。