[解決済み] Viola-Jonesの顔検出は180kの特徴を主張する

質問

私は Viola-Jonesの顔検出アルゴリズム . この技術は、画像内に 24x24 ピクセルのサブフレームを配置し、その後、その中に長方形の特徴をあらゆる位置、あらゆるサイズに配置することに依存しています。

これらの特徴は、2つ、3つ、または4つの矩形で構成されます。次のような例があります。

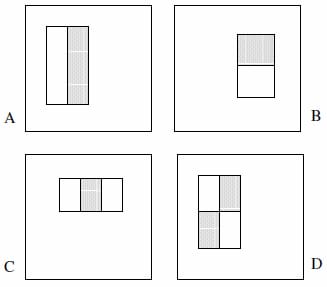
彼らは、網羅的なセットは180k以上であると主張しています（セクション2）。

検出器の基本解像度が24x24であることを考えると、矩形特徴の網羅的な集合は180,000以上と非常に大きいことがわかります。Haar基底とは異なり、矩形特徴のセットは過完了であることに注意してください。 とは異なり，矩形特徴のセットは過完了であることに注意してください．

以下の記述は、論文に明示されていないため、私の思い込みです。

1. 2角形の特徴が2つ、3角形の特徴が2つ、4角形の特徴が1つだけある。という論理で観測しています。 差分 を観察しているのであって、色や輝度やその種の何かを明示的に観察しているのではないということです。
2. 特徴タイプ A を 1x1 ピクセルのブロックとして定義することはできず、少なくとも 1x2 ピクセル以上でなければなりません。また、タイプ D は少なくとも 2x2 ピクセルでなければならず、このルールは他の特徴についても同様に適用されます。
3. 特徴量タイプAは、中央のピクセルが分割できないため、1x3ピクセルのブロックとして定義できず、それを自分から引くと1x2ピクセルのブロックと同じになる。この特徴量タイプは、偶数幅でのみ定義される。また、特徴量タイプCの幅は3で割り切れるものでなければならず、このルールは他の特徴量にも適用される。
4. 幅と高さの両方が0の素性は定義できないので、繰り返し x と y を24から機能の大きさを引いた値にします。

これらの仮定に基づき、網羅的なセットを数えてみました。

const int frameSize = 24;
const int features = 5;
// All five feature types:
const int feature[features][2] = {{2,1}, {1,2}, {3,1}, {1,3}, {2,2}};

int count = 0;
// Each feature:
for (int i = 0; i < features; i++) {
    int sizeX = feature[i][0];
    int sizeY = feature[i][1];
    // Each position:
    for (int x = 0; x <= frameSize-sizeX; x++) {
        for (int y = 0; y <= frameSize-sizeY; y++) {
            // Each size fitting within the frameSize:
            for (int width = sizeX; width <= frameSize-x; width+=sizeX) {
                for (int height = sizeY; height <= frameSize-y; height+=sizeY) {
                    count++;
                }
            }
        }
    }
}

結果は 162,336 .

Viola & Jones が話す「180,000 以上」の値を近似するために私が見つけた唯一の方法は、仮定 #4 を削除することと、コードにバグを導入することです。これは、4 つの行をそれぞれ次のように変更することを含みます。

for (int width = 0; width < frameSize-x; width+=sizeX)
for (int height = 0; height < frameSize-y; height+=sizeY)

その結果 180,625 . (これは、機能がサブフレームの右側および/または下側に接触するのを効果的に防ぐことになることに注意してください)。

ここでもちろん疑問があります。彼らは実装で間違いを犯したのでしょうか。サーフェスが 0 のフィーチャーを考慮することは意味があるのでしょうか。それとも、私の見方が間違っているのでしょうか?

どのように解決するのですか?

よく見ると、あなたのコードは私には正しく見えます。これは、オリジナルの作者が1つ違いのバグを持っていたかどうかを疑わせます。誰かが OpenCV がそれをどのように実装しているかを見るべきだと思います!

それにもかかわらず、理解しやすくするための一つの提案は に対して ループの順番を入れ替え、まずすべてのサイズを調べ、次にサイズが与えられた可能な場所をループすることです。

#include <stdio.h>
int main()
{
    int i, x, y, sizeX, sizeY, width, height, count, c;

    /* All five shape types */
    const int features = 5;
    const int feature[][2] = {{2,1}, {1,2}, {3,1}, {1,3}, {2,2}};
    const int frameSize = 24;

    count = 0;
    /* Each shape */
    for (i = 0; i < features; i++) {
        sizeX = feature[i][0];
        sizeY = feature[i][1];
        printf("%dx%d shapes:\n", sizeX, sizeY);

        /* each size (multiples of basic shapes) */
        for (width = sizeX; width <= frameSize; width+=sizeX) {
            for (height = sizeY; height <= frameSize; height+=sizeY) {
                printf("\tsize: %dx%d => ", width, height);
                c=count;

                /* each possible position given size */
                for (x = 0; x <= frameSize-width; x++) {
                    for (y = 0; y <= frameSize-height; y++) {
                        count++;
                    }
                }
                printf("count: %d\n", count-c);
            }
        }
    }
    printf("%d\n", count);

    return 0;
}

と同じ結果で、前の 162336

それを検証するために、4x4 のウィンドウの場合をテストし、すべての場合を手動でチェックしました (1x2/2x1 と 1x3/3x1 の形状は 90 度回転しただけで同じなので数えやすかったです)。

2x1 shapes:
        size: 2x1 => count: 12
        size: 2x2 => count: 9
        size: 2x3 => count: 6
        size: 2x4 => count: 3
        size: 4x1 => count: 4
        size: 4x2 => count: 3
        size: 4x3 => count: 2
        size: 4x4 => count: 1
1x2 shapes:
        size: 1x2 => count: 12             +-----------------------+
        size: 1x4 => count: 4              |     |     |     |     |
        size: 2x2 => count: 9              |     |     |     |     |
        size: 2x4 => count: 3              +-----+-----+-----+-----+
        size: 3x2 => count: 6              |     |     |     |     |
        size: 3x4 => count: 2              |     |     |     |     |
        size: 4x2 => count: 3              +-----+-----+-----+-----+
        size: 4x4 => count: 1              |     |     |     |     |
3x1 shapes:                                |     |     |     |     |
        size: 3x1 => count: 8              +-----+-----+-----+-----+
        size: 3x2 => count: 6              |     |     |     |     |
        size: 3x3 => count: 4              |     |     |     |     |
        size: 3x4 => count: 2              +-----------------------+
1x3 shapes:
        size: 1x3 => count: 8                  Total Count = 136
        size: 2x3 => count: 6
        size: 3x3 => count: 4
        size: 4x3 => count: 2
2x2 shapes:
        size: 2x2 => count: 9
        size: 2x4 => count: 3
        size: 4x2 => count: 3
        size: 4x4 => count: 1