TensorFlow入門学習(機械・アルゴリズムに選択を手伝ってもらう)
カタログ
0. Personal understanding
1. basic use
2. Introduction to MNIST (multiclass classification)
3. deeper into MNIST
4. convolutional neural network: classification of CIFAR-10 dataset
5. Vector Representations of Words (VOR)
6. Recurrent Neural Networks (RNN), LSTM (Long-Short Term Memory, LSTM)
7. building a chatbot with deep learning networks
<スパン 0.個人的な理解
学習開始時に、ディープリーンリングとニューラルネットワークの大まかな理解をここに書いておきます。
1. deep learning neural network is essentially in lean what, I think is in learn a set of parameters, or selection mode, which is often said to be a classifier, this classifier may be a high-dimensional classifier, composed of a set of parameters
2. take image captcha recognition, the parameters here means the distribution of weights in the image area (the distribution of weight pixel space is different for number 1 and number 2), if we select the pixel space of the image (e.g. 32 * 32) + RGB color channel (3) as input features (essentially this is feature engineering), these features will be treated as neurons by tensorflow and at each layer these neurons are combined and the results are calculated, while the neurons of the next layer of the neural network, the output of this layer will be combined again, the combination, according to the accuracy of the last prediction, will automatically give each combination a different weight (weight) by back propogation, this process will continue until the adjustment of a best-fit weight, which is often the pixel space weight that is closest to the real image
3. . All things in the world can be abstracted into a high-dimensional matrix, and this process will have different ways of extracting abstraction in different domains, i.e., feature engineering, and it is worth noting that having expertise in the corresponding domain is very helpful for the implementation of feature engineering
4. after we abstract the domain-specific, objects to be classified/recognized as a high-dimensional matrix, into the deep learn algorithm model becomes a neuron (node), the next thing to do in the deep learn model is called "fitting"
5. To complete the classification and recognition, the goal of deep learn is to find a fit matrix (figuratively speaking, "high-dimensional-1 classification cut "), to achieve this purpose, 3 elements are needed
1) the fit function (activation function): used to generate the fitted cut
2) error function (Loss Function): used in the process of network computation to calculate the distance of the fitted cut from the optimal value of the current fitted parameters, in order to adjust the parameters at any time
3) neural network structure: deep learn deep learning and ordinary neural networks is the difference between "layers ", deep neural networks often have more than 3 layers (input layer, hidden layer, output layer), when the number of layers increases, in each layer to choose how the combination of cross structure becomes a difficult thing, there is no sound theoretical support can accurately There is no sound theoretical support to precisely calculate what kind of network structure can output the best results, and the usual practice is to keep trying different network structures according to the business scenario that we do not agree with, until we "try out" a relatively good network structure, and then make parameter adjustments on top of this network structure
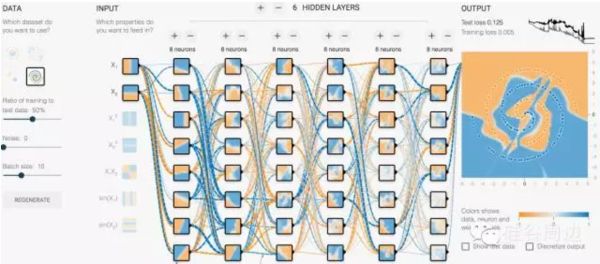
注目すべきは、ニューラルネットワークの大きな魔法は、多くの種類の特徴を正確に抽出できなくても、ニューラルネットワークとニューロンの十分な層があれば、ニューラルネットワーク自身が有用な特徴を組み立ててくれることです。これは、ある実験を見ればわかることです。
http://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=spiral®Dataset=reg-plane&learningRate=0.03® ularizationRate=0&noise=0&networkShape=8,8,8,8,8,8,8&seed=0.33671&showTestData=false&discretize=false& percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false& cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false
入力には2次元の特徴量x1,x2のみを与え、1層あたり8ニューロンの6層ニューラルネットワークを選択する。ネットワークの各層で、次元は8つに拡張される。ニューラルネットワークは、学習中に自動的に自分にとって価値のある次元を探し、ある重みを与え、最適なDLを見つけるまで損失関数に従って再帰的に下降し続けるので、特徴エンジニアリングの難易度を大幅に下げることができます。
<スパン <スパン 0x1: ニューラルネットワークが本当に理解していること
One, the neural network understands how to decouple the input space into a hierarchical set of convolutional filters
Second, the neural network understands the probabilistic mapping from a set of filters to a set of specific labels. What the neural network learns is not at all what it means to "see" in the human sense, and it certainly does not mean, in scientific terms, that we have solved the problem of computer vision
畳み込みニューラルネットワークが学習する入力空間の階層的切り離しは、人間の視覚野の振る舞いを模倣していると言う人がいる。この主張は正しいかもしれないし、正しくないかもしれない。しかし、それを認めるか否定するか、比較的強い証拠があることは今のところ不明である。もちろん、人間の視覚野が同じような方法で物事を学習し、何らかの形でこれは我々の視覚世界の自然なデカップリングであると期待する人もいるだろう(ちょうどフーリエ変換が周期的な音信号の自然なデカップリングであるように)[ここで、音信号のフーリエ変換が、異なる周波数の音信号があることを非常に自然かつ物理的に理解していることを示しているように、我々の 視覚情報の認識は層で行われる、丸いのが車輪、4輪あるのが自動車、かっこいいのがスポーツカー、こんな感じだ]。しかし、人間の視覚信号のフィルタリング、レイヤー化、処理の性質は、私たちの弱い鶏の畳み込みネットワークと全く同じものではない可能性が高いのです。視覚野は層状ではあるが畳み込み式ではなく、その層は皮質のカラムの構造を持っており、その構造の真の目的は現時点では不明で、我々の人工神経ネットワークにはまだない構造である(ジョー大王ことジェフ・ヒントンはその研究に取り組んでいるが)。さらに、人間には静止画像を分類する以外にも多くの視覚パーセプトロンがあり、これらのパーセプトロンは静的で受動的ではなく、連続的で能動的であり、これらの受容体も眼球運動などの複数のメカニズムによって複雑に制御されています
<スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン 関連リンク
https://groups.google.com/a/tensorflow.org/forum/#!forum/discuss
https://stackoverflow.com/questions/tagged/tensorflow
http://www.tensorfly.cn/tfdoc/resources/overview.html
https://www.zhihu.com/question/41667903
http://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=spiral®Dataset=reg-plane&learningRate=0.03® ularizationRate=0&noise=0&networkShape=8,8,8,8,8,8,8&seed=0.33671&showTestData=false&discretize=false& percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false& cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false
<スパン 1. 基本的な使用方法
<スパン <スパン 0x1: 概要
1. Use a graph to represent a computational task. 2.
2. Execute the graph in a context called a session. 3.
3. Use tensor to represent data. 4.
4. maintain state through variables. 5.
5. use feed and fetch to assign values to or retrieve data from arbitrary operations.
TensorFlowは、グラフを使って計算タスクを表現するプログラミングシステムである。グラフのノードはop(operationの略)と呼ばれる。opは0個以上のTensorを取得し、計算を実行し、0個以上のTensorを生成する。各Tensorは型付き多次元配列である。例えば、小さな画像の集合を、[batch, height, width, channels]という4次元の浮動小数点数の配列として表現することができる。
TensorFlowのグラフは、計算の過程を記述したものである。計算を実行するには、グラフをセッションで起動する必要がある。セッションはグラフのopをCPUやGPUなどのデバイスに分配し、opを実行するためのメソッドを提供する。これらのメソッドが実行された後、結果のテンソルが返される。Pythonではnumpyのndarrayオブジェクト、CやC++ではtensorflow::Tensorインスタンスとして返される。
0x2: 計算表
TensorFlowのプログラムは、通常、ビルドフェーズと実行フェーズに分かれて構成される。構築フェーズでは、opの実行ステップをグラフとして記述する。実行フェーズでは、実行グラフ内のopをセッションを用いて実行する。
例えば、構築フェーズでニューラルネットワークを表現・学習するためのグラフを作成し、実行フェーズでグラフ内の学習opを繰り返し実行するのが一般的である。
<スパン 1. グラフの構築(分類する対象を高次元行列に抽象化する)。
グラフを構成する最初のステップは、ソースオペを作成することである。ソースオペは、定数などの入力を必要としない。ソースオペの出力は、他のオペに渡されて計算される。
Pythonライブラリでは、opコンストラクタの戻り値は構築されたopの出力を表し、これらの戻り値は入力として他のopコンストラクタに渡すことができます。
# -*- coding:utf-8 -*-
import tensorflow as tf
if __name__ == "__main__":
# Create a constant op, producing a 1x2 matrix. This op is treated as a node
# Add to the default graph.
#The
# The return value of the constructor represents the return value of the constant op.
matrix1 = tf.constant([[3., 3.]])
# Create another constant op, producing a 2x1 matrix.
matrix2 = tf.constant([[2.], [2.]])
# Create a matrix multiplication matmul op , taking 'matrix1' and 'matrix2' as input.
# The return value 'product' represents the result of the matrix multiplication.
product = tf.matmul(matrix1, matrix2)
デフォルトのグラフは、3つのノード、2つのconstant() op、そしてmatmul() opを持つようになりました。実際に行列を掛け合わせてその結果を得るためには、グラフをセッションで起動する必要があります。
2. セッションでグラフを開始する
ダイアグラムは、構築段階が完了するまで開始されません。ダイアグラムを開始する最初のステップは、Session オブジェクトを作成することです。作成パラメータがない場合、セッション・コンストラクターは、デフォルトのダイアグラムを開始します。
# -*- coding:utf-8 -*-
import tensorflow as tf
if __name__ == "__main__":
# Create a constant op, producing a 1x2 matrix. This op is treated as a node
# Add to the default graph.
#The
# The return value of the constructor represents the return value of the constant op.
matrix1 = tf.constant([[3., 3.]])
# Create another constant op, producing a 2x1 matrix.
matrix2 = tf.constant([[2.], [2.]])
# Create a matrix multiplication matmul op , taking 'matrix1' and 'matrix2' as input.
# The return value 'product' represents the result of the matrix multiplication.
product = tf.matmul(matrix1, matrix2)
# The default graph now has three nodes, two constant() op, and one matmul() op. In order to actually multiply the matrices and get the result of the matrix multiplication, you must start the graph in a session.
# Start the default graph.
sess = tf.Session()
# Call the 'run()' method of sess to perform the matrix multiplication op, passing 'product' as an argument to the method.
# As mentioned above, 'product' represents the output of the matrix multiplication op, and passing it in indicates to the method that we want to retrieve
# The output of the matrix multiplication op.
# The entire execution is automated.
# The entire execution is automated, and the session is responsible for passing all the input needed for the op. The op is usually executed concurrently.
#
# The function call 'run(product)' triggers the execution of the three op's in the diagram (two constant op's and a matrix multiplication op).
#
# The return value 'result' is a numpy `ndarray` object.
result = sess.run(product)
print result
# ==> [[ 12.]]
# Task complete, close the session.
sess.close()
実装面では、TensorFlowはグラフの定義を、利用可能なコンピューティングリソース(CPUやGPUなど)を活用する分散実行操作に変換する。通常、CPUとGPUのどちらを使うかは明示的に指定する必要はなく、TensorFlowが自動的に検出することができます。GPUが検出された場合、TensorFlowは可能であれば最初に見つけたGPUを使用して処理を実行します

<スパン 0x3: テンソル
TensorFlowのプログラムでは、計算グラフのすべてのデータをテンソルデータ構造で表現し、演算と演算の間に渡されるデータもすべてテンソルである。TensorFlowのテンソルは、n次元の配列やリストと考えることができる。テンソルは静的な型であるrankと、形状を含む。
<スパン 0x4: 変数
変数とは、実行中のグラフの状態に関する情報を保持するものです。次の例は、変数を使って簡単なカウンターを実装する方法を示しています。
# -*- coding:utf-8 -*-
import tensorflow as tf
if __name__ == "__main__":
# Create a variable, initialize to scalar 0.
state = tf.Variable(0, name="counter")
# Create an op, which increments state by 1
one = tf.constant(1)
new_value = tf.add(state, one)
update = tf.assign(state, new_value)
# After starting the graph, the variables must first be initialized by the `initialize` (init) op,
# First an `initialize` op must be added to the graph.
init_op = tf.initialize_all_variables()
# Start the graph, run the op
with tf.Session() as sess:
# run 'init' op
sess.run(init_op)
# Print the initial value of 'state'
print sess.run(state)
# Run the op, update 'state', and print 'state'
for _ in range(3):
sess.run(update)
print sess.run(state)

コード中のassign()操作は、add()操作と同様に、図に描かれた式の一部です。したがって、run()が呼び出されて式が実行されるまで、実際にassign操作が行われるわけではありません。
統計モデルのパラメータは、変数の集合として表現するのが一般的である。例えば、ニューラルネットワークの重みをある変数としてテンソルに格納することができる。学習中、このテンソルは学習グラフを繰り返し実行することで更新される。
0x5: フェッチ
操作の出力を取得するために、Sessionオブジェクトのrun()呼び出しを使ってグラフを実行する際に、いくつかのテンソルを渡すことができ、これらのテンソル
を使用すると、結果を取得するのに役立ちます。前の例では、単一のノードの状態を取得しただけでしたが、複数のテンソルを取得することもできます。
# -*- coding:utf-8 -*-
import tensorflow as tf
if __name__ == "__main__":
# Start the default graph.
sess = tf.Session()
input1 = tf.constant(3.0)
input2 = tf.constant(2.0)
input3 = tf.constant(5.0)
intermed = tf.add(input2, input3)
mul = tf.multiply(input1, intermed)
with tf.Session():
result = sess.run([mul, intermed])
print result

<スパン 0x6: フィード
上記の例では、テンソルを定数または変数として格納し、計算グラフに導入している。TensorFlowはまた、グラフ内の任意の操作でテンソルを一時的に置き換えることができるフィード機構を提供する。
フィードは一時的に操作の出力をテンソル値で置き換える。run() 呼び出しの引数としてフィードデータを提供することができる。フィードはそれを呼び出したメソッドに対してのみ有効であり、メソッドが終了するとフィードは消滅する。最も一般的な使用例は、いくつかの特殊な操作を "フィード" 操作として指定することで、tf.placeholder() を使用してそれらの操作のプレースホルダを作成することでマークされる。
# -*- coding:utf-8 -*-
import tensorflow as tf
if __name__ == "__main__":
input1 = tf.placeholder(tf.types.float32)
input2 = tf.placeholder(tf.types.float32)
output = tf.multiply(input1, input2)
with tf.Session() as sess:
print sess.run([output])
print sess.run([output], feed_dict={input1:[7.], input2:[2.]})
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
<スパン
0x7: バッチ
<スパン ディープラーニングの最適化アルゴリズムは、ざっくり言うと「勾配降下法」です。毎回パラメータを更新する方法は2つあります。
1. the first, traverse the entire data set to calculate the loss function once, and then calculate the gradient of the function for each parameter, update the gradient. This method looks at all the samples in the dataset for each parameter update, which is computationally overhead, slow, and does not support online learning, which is called Batch gradient descent.
This is called stochastic gradient descent, which is faster, but the convergence performance is not so good, and it may wander around the optimal point and not hit the optimal point. The two parameter updates may also cancel each other out, causing the target function to oscillate more violently
両者の欠点を克服するために、現在では、データをバッチに分割し、バッチごとにパラメータを更新することで、バッチのデータセットが共同でこの勾配の方向を決定し、ディセントが暴走してランダム性を低下させることが少ない、ミニバッチ勾配ディセントという妥協策が一般に用いられている。一方、バッチのサンプルサイズはデータセット全体と比較して非常に小さいため、計算量はそれほど大きくはありません
基本的に最近の勾配降下はミニバッチが基本で、モジュールにもbatch_sizeがよく出てきますが、これはこれを指しています。
コードでよく目にするオプティマイザ、SGDはstochastic gradient descentの略ですが、1サンプルに1回更新されるということではなく、やはりミニバッチがベースになっています
<スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン 関連リンク
http://www.tensorfly.cn/tfdoc/get_started/os_setup.html
http://keras-cn.readthedocs.io/en/latest/getting_started/concepts/#batch
<スパン 2. MNIST(多クラス分類)を使ってみよう
<スパン <スパン 0x1: MNISTデータセット
https://tensorflow.googlesource.com/tensorflow/+/master/tensorflow/examples/tutorials/mnist/input_data.py#
ダウンロードしたデータセットは、6万行の学習用データセット(mnist.train)と1万行のテスト用データセット(mnist.test)に分割されています。このような切り分けは重要で、テスト用データセットは訓練用ではなく、機械学習モデル設計時にモデルの性能を評価するために使用する必要があり、設計したモデルを他のデータセットに汎化(generalization)しやすくするためだそうです。
前述したように、MNISTの各データユニットは、手書き数字を含む画像とそれに対応するラベル(正しくラベル付けされたサンプルは教師あり学習で特に重要)の2つの要素を持っている。これらの画像をquot;xs"、これらのラベルをquot;ys"とする。学習データセットとテストデータセットの両方がxsとysを含んでおり,例えば,学習データセットの画像はmnist.train.images,学習データセットのラベルはmnist.train.labelsである.
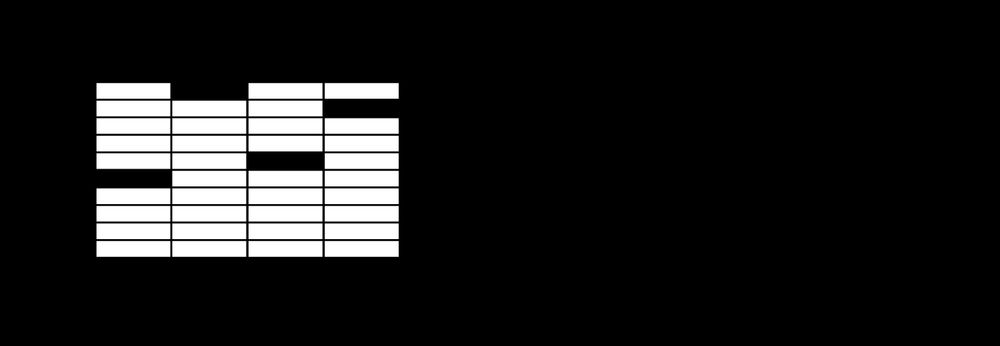
各画像は28ピクセル×28ピクセルで構成されています。でこの画像を数値の配列で表すことができる。

この配列を長さ28x28=784のベクトルに展開する。個々の画像が同じように展開されていれば、配列の展開方法(数字の並び順)は関係ありません。このように考えると、MNISTデータセットの画像は784次元のベクトル空間の点であり、比較的複雑な構造を持っていることがわかります(注意:このようなデータの可視化には計算量が必要です)。
画像の数値の配列を平坦化すると、画像の2次元構造に関する情報が失われる。これは明らかに望ましくないことであり、最良のコンピュータビジョン手法はこの構造情報を掘り起こして利用することになるが、現在のロック学習の単純な数学モデルであるソフトマックス回帰では、この構造情報を利用することはない。
このように、MNIST学習データセットにおいて、mnist.train.imagesは形状[60000, 784]のテンソルであり、1次元目の数値が画像のインデックスに、2次元目の数値が各画像の画素点のインデックスに使用されています。このテンソルの各要素は、特定の画像の画素の強度値を0から1までの値で表している(白黒画像)。

対応するMNISTデータセットのラベルは0から9までの数字で、与えられた画像に表された数字を表現するために使用される。このチュートリアルで使用するために、ラベル付きデータを"one-hot vectors"とすることにします。ワンホットベクトルとは、1次元を除くすべての次元で0であるため、このチュートリアルでは、数nは、(0から始まる)n次元にのみ数1を持つ10次元ベクトルとして表現されることになります。例えば、ラベル 0 は ([1,0,0,0,0,0,0,0,0,0,0]) のように表現されます。したがって,mnist.train.labels は [60000, 10] の数値行列である.
<スパン 0x2: ソフトマックスリグレッション
MNISTの各画像は0から9までの数字を表していることが分かっています。我々はある画像がそれぞれの数字を表す確率を求めたい。例えば、9を含む画像は80%の確率で9を表し、5%の確率で8と判断し(8も9も上半分に小さな丸があるため)、他の数字を表す確率はより小さい値を与えると推測します。
これは、ソフトマックス回帰モデルを使用した典型的な例です。ソフトマックスモデルは、異なるオブジェクトに確率を割り当てるために使用することができます。後に、より洗練されたモデルを学習する際にも、最後のステップで確率を割り当てるためにソフトマックスを必要とします。
softmax回帰には2つのステップがあります。
<スパン 1. 第 1 段階
ある画像が特定の数値クラスに属するという根拠を得るために、画像の画素値に重み付けをし、それらを合計します。もしその画素が、画像がそのクラスに属さないという強い証拠を持っていれば、対応する重みは負になり、逆にその画素が、画像がそのクラスに属するという有利な証拠を持っていれば、その重みは正になります。
下図は、ある数値クラスについて、画像上の各画素にモデルが学習する重みを示したものである。赤は負の重み、青は正の重みを表す。
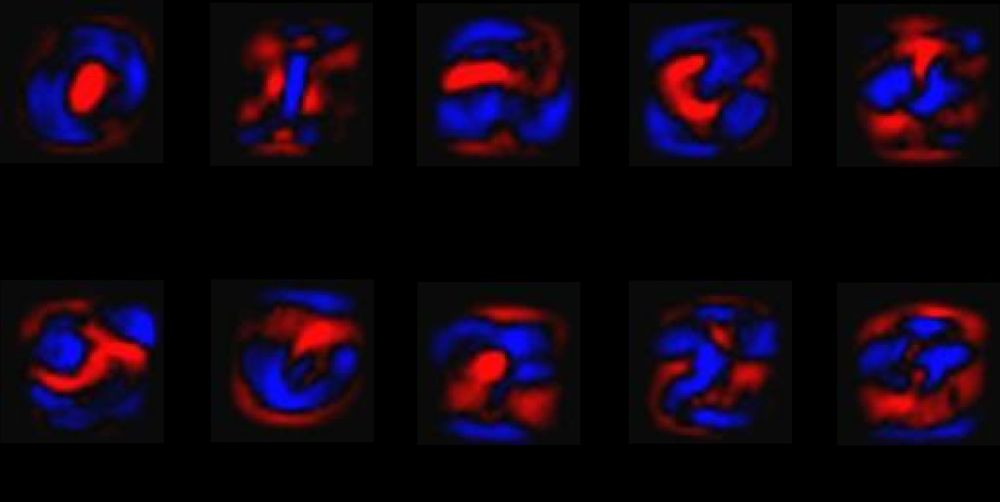
また、入力には余計な干渉が伴うことが多いので、バイアス(偏り)を追加する必要がある。そこで、与えられた入力画像xに対して、数iが次のように表せるという証拠を表します。
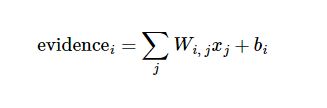
どこ はウェイトを表し は数を表します。 i クラスのオフセット j は、与えられた画像を表す <スパン x 画素のインデックスは画素の総和に使用される。この証拠は,ソフトマックス関数を用いて確率に変換することができます。 y :
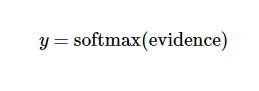
ここでソフトマックスは、定義した一次関数の出力を、10個の数字のクラスに対する確率分布という望む形式に変換する活性化またはリンク関数と考えることができる。したがって、画像があれば、各数値に対する適合度は、ソフトマックス関数によって確率値に変換することができます。
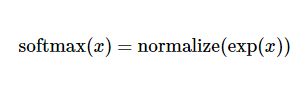
右辺の下式を展開すると、次のようになります。
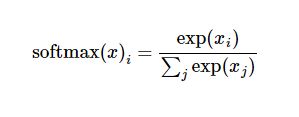
しかし、より多くの場合、ソフトマックスモデル関数は前者の形で定義される。入力値をべき乗指数で評価し、その結果得られた値を正則化するのである。このべき乗演算は、証拠が大きければ大きいほど、仮説モデル(仮説)内部の乗法重みの値が大きくなることを示す。逆に、エビデンスが少ないということは、仮説モデル内部の乗法係数が小さくなることを意味する。そして、Softmaxはこれらの重みの和が1になるように正則化し、有効な確率分布を構築する。
ソフトマックス回帰モデルは、以下のグラフで説明することができます。
xs
を加重加算し、それぞれにバイアスを加え、最後にソフトマックス関数に入力する。

これを方程式で書くと、次のようになります。

また、この計算過程をベクトルで表現することもできます。行列の乗算やベクトルの和を利用するのです。これは、計算をより効率的にするのに役立ちます。(また、より効率的に考えることができます)。

さらに一歩進んで、もっとコンパクトに書くこともできます。
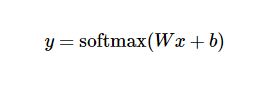
つまり、人間の言葉を認識するプロセスは、多くの人、様々な書き方、様々なフォントの言葉を見て、人間の脳の中で、ある言葉が「どのような」ものであるべきか、重みのある認知モデルが形成されるのである。この認知プロセスを数学的概念に抽象化すると、特定の画素領域に高い重みを与え、その画素の重みに応じて領域を分割し、その領域にほぼ入っている限り、その単語である確率が高くなるはずである。
0x3: 回帰モデルの実装
y = tf.nn.softmax(tf.matmul(x,W) + b)
TensorFlowは、ソフトマックス回帰モデルの計算を特に簡単にするだけでなく、機械学習モデルから物理シミュレーションモデルまで、他の様々な数値計算をこの非常に柔軟な方法で記述することができるのです。一度定義したモデルは、コンピュータのCPU、GPU、あるいは携帯電話など、さまざまなデバイスで実行することができます。
<スパン 0x4: 学習モデル
モデルを学習させるためには、まず、そのモデルが優れているかどうかを評価するための指標を定義する必要があります。実は、機械学習では、モデルが悪いことを示す指標(コストや損失と呼ばれる)を定義し、その指標を最小化しようとするのが一般的である。しかし、この2つのアプローチは同じである。
非常に一般的で素晴らしいコスト関数に、quot;cross-entropy"があります。クロスエントロピーは情報理論における情報圧縮符号化の技術から生まれたが、その後、ゲーム理論から機械学習まで他の分野でも重要な技術に発展している。以下のように定義されている。
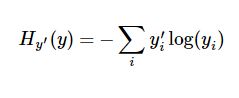
y は予測の確率分布です。 y' は実際の分布(入力した一発ベクトル)です。もっと単純に理解すると、クロスエントロピーは、真実を記述するための予測の非効率性を測定するために使われます。 . つまり、我々の記述が不正確であればあるほど、不確実性が高くなり、エントロピー値も高くなるのです
TensorFlow has a graph that describes your individual computational units, and it can automatically use the backpropagation algorithm to efficiently determine how your variables affect the value of that cost you want to minimize. TensorFlow then uses the optimization algorithm you choose to continuously modify the variables to reduce the cost.
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
ここでは、TensorFlowに勾配降下アルゴリズムを用いて、学習率0.01でクロスエントロピーを最小化するように依頼しています。勾配降下アルゴリズムは、TensorFlowが単純にコストを抑える方向に各変数を少しずつ動かしていくだけのシンプルな学習処理です
TensorFlowがここで実際に行っているのは、バックプロパゲーションアルゴリズムと勾配降下アルゴリズムを実装するために、計算を記述したグラフの背景に新しい計算ユニットの束を追加することです。そして、あなたに返すのは1つの演算で、その演算を実行すると、勾配降下アルゴリズムでモデルを訓練し、変数を微調整して、コストを下げ続けるのです。
<スパン 0x5: モデルの評価
tf.argmaxは、ある次元のあるテンソルオブジェクトのデータ(softmaxは[1,0,0,0,0,0,0,0]という行列を予測し、1に相当するものが最大確率で予測した数値)の最大値があるインデックス値を与える非常に便利な関数です(数に相当する部分)。ラベルベクトルは0,1から構成されるので、1の最大値が位置するインデックス位置がカテゴリラベルとなる。例えば、tf.argmax(y,1)は任意の入力xに対してモデルが予測したラベル値を返し、tf.argmax(y_,1)は正しいラベルを表すので、我々の予測が真のラベルマッチであるかどうか(インデックス位置が同じならマッチ)を確認するにはtf.equalを使うことができる。
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
このコードの行は、ブーリアン値のセットを提供します。正しく予測された項目の割合を求めるには、ブーリアン値を浮動小数点数に変換して、その平均をとればよい。たとえば
[True, False, True, True]
は次のようになります。
[1,0,1,1]
とし、平均化すると
0.75
.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
最後に、テストデータセットの上で学習したモデルの正しさを計算する。
print sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})
<スパン 0x6: mnist_softmax.py
# Copyright 2015 The TensorFlow Authors.
#All Rights Reserved.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for
関連
-
[解決済み】TensorFlowで*.pbファイルを使用する方法とその動作は?
-
[解決済み] tf.global_variables_initializerは何のためにあるのですか?
-
[解決済み] モジュール 'tensorflow' には 'logging' という属性がありません。
-
[解決済み] tensorboard: コマンドが見つかりません。
-
[解決済み] ImportError: libcudart.so.8.0: 共有オブジェクト・ファイルを開くことができません。そのようなファイルまたはディレクトリがありません
-
TensorFlow cnn-cifar10 サンプルコード詳細
-
AttributeError: モジュール tensorflow には属性プレースホルダーがありません。
-
Bishopの問題2: tf-pose-estimation-master, last ModuleNotFoundError: tensorflow.contrib'という名前のモジュールがありません(解決済み)。
-
テンソルフロー学習ノート(II): テンソル変換
-
tf.convert_to_tensorを使用したときの値のエラーの解決方法
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
[解決済み】ImportError: 名前 'abs' をインポートすることができません。
-
徹底的な解決。お使いのCPUは、このTensorFlowバイナリが使用するためにコンパイルされていない命令をサポートしています。AVX2
-
[解決済み] Tensorflowです。tf.expand_dimsはいつ使うの?
-
[解決済み] Tensorflowにおけるglobal_stepの意味とは?
-
[解決済み] tf.int64をtf.float32に変換する方法は?
-
[解決済み] 入力パイプラインは、keras.utils.Sequenceオブジェクトまたはtf.data.Datasetを使用しますか?
-
[解決済み] tf.nn.reluの "relu "とは何の略ですか?
-
[解決済み] tf.keras.Inputで形状を理解する?
-
AttributeError: モジュール 'tensorflow' には 'placeholder' という属性がないことを解決する。
-
Tensorflowの実行エラー。tensorflow.contrib'という名前のモジュールがありません。
















