[解決済み] scipyで2次元補間を行うには？

2022-09-05 15:30:13

質問

このQ&Aは、scipyを使った二次元（および多次元）補間に関する標準的な（っぽい）ものです。また、多次元補間法の基本的な構文に関する質問もよくありますので、これらも整理しておきたいと思います。

私は散在する2次元のデータ点のセットを持っており、それらを美しい曲面としてプロットしたいと思います。 contourf または plot_surface で matplotlib.pyplot . scipyを使って2次元や多次元のデータをメッシュに補間するにはどうしたらいいですか？

を見つけたのですが scipy.interpolate サブパッケージは見つけましたが interp2d または bisplrep または griddata または RBFInterpolator (または、より古い Rbf ). これらのメソッドの適切な構文は何ですか？

どのように解決するのですか？

免責事項: 私はほとんど構文上の考慮事項と一般的な動作を念頭に置いて、この記事を書いています。私は説明されている方法のメモリと CPU の側面には詳しくないので、この回答は、補間の品質が考慮すべき主な側面であるような、適度に小さいデータセットを持っている人を対象としています。非常に大きなデータセットを扱う場合、より性能の良い方法（すなわち griddata と RBFInterpolator がない場合 neighbors キーワード引数なし) は実行可能ではないかもしれません。

この回答では、新しい RBFInterpolator クラスで導入された SciPy 1.7.0 . レガシーの場合 Rbf クラスはこの回答の前のバージョン .

3種類の多次元補間法を比較してみますね( interp2d /splines。 griddata と RBFInterpolator ). ここでは、2種類の補間タスクと2種類の基礎関数（補間される点）を対象とする。具体的な例として2次元の補間を示すが，実行可能な方法は任意の次元に適用できる．各手法は様々な種類の補間を提供しますが，私はすべてのケースで3次補間（またはそれに近いもの ¹ ). 重要なのは、補間を行うときは常に、生データと比較してバイアスがかかること、そして使用する特定の方法が最終的に得られるアーティファクトに影響を与えるということです。このことを常に意識し、責任を持って補間してください。

2つの補間タスクは

アップサンプリング（入力データは矩形グリッド、出力データは高密度グリッド）
散布されたデータの規則的なグリッドへの補間

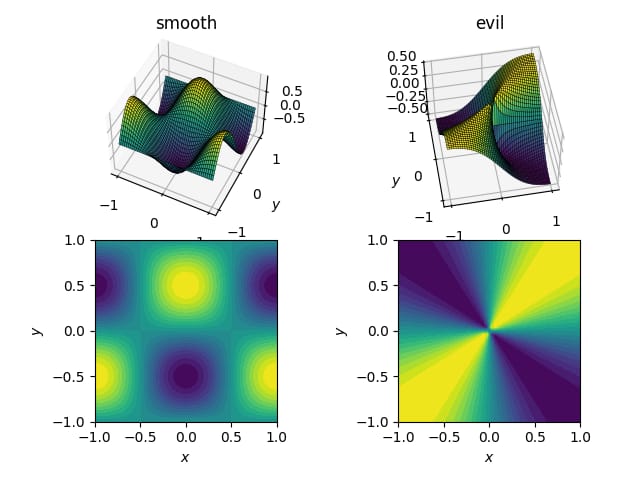
2つの関数（ドメイン上 [x, y] in [-1, 1]x[-1, 1] ) は

は、スムーズで親切な機能です。 cos(pi*x)*sin(pi*y) での範囲 [-1, 1]
は邪悪な（特に、非連続的な）関数です。 x*y / (x^2 + y^2) で、原点付近で 0.5 の値を持ち、範囲は [-0.5, 0.5]

こんな感じです。

まず、これらの4つのテストの下で3つのメソッドがどのように動作するかを示し、次に3つのメソッドの構文を詳しく説明します。メソッドに何を期待すべきかを知っていれば、その構文を学ぶのに時間を浪費したくないかもしれません (あなたのことを見ています。 interp2d ).

テストデータ

説明のために、入力データを生成したコードを示します。この特定のケースでは、私は明らかにデータの基礎となる関数を認識していますが、私は補間メソッドの入力を生成するためにのみこれを使用します。私は便宜上numpyを使用していますが（そしてほとんどデータを生成するために）、scipyだけでも十分でしょう。

import numpy as np
import scipy.interpolate as interp

# auxiliary function for mesh generation
def gimme_mesh(n):
    minval = -1
    maxval =  1
    # produce an asymmetric shape in order to catch issues with transpositions
    return np.meshgrid(np.linspace(minval, maxval, n),
                       np.linspace(minval, maxval, n + 1))

# set up underlying test functions, vectorized
def fun_smooth(x, y):
    return np.cos(np.pi*x) * np.sin(np.pi*y)

def fun_evil(x, y):
    # watch out for singular origin; function has no unique limit there
    return np.where(x**2 + y**2 > 1e-10, x*y/(x**2+y**2), 0.5)

# sparse input mesh, 6x7 in shape
N_sparse = 6
x_sparse, y_sparse = gimme_mesh(N_sparse)
z_sparse_smooth = fun_smooth(x_sparse, y_sparse)
z_sparse_evil = fun_evil(x_sparse, y_sparse)

# scattered input points, 10^2 altogether (shape (100,))
N_scattered = 10
rng = np.random.default_rng()
x_scattered, y_scattered = rng.random((2, N_scattered**2))*2 - 1
z_scattered_smooth = fun_smooth(x_scattered, y_scattered)
z_scattered_evil = fun_evil(x_scattered, y_scattered)

# dense output mesh, 20x21 in shape
N_dense = 20
x_dense, y_dense = gimme_mesh(N_dense)

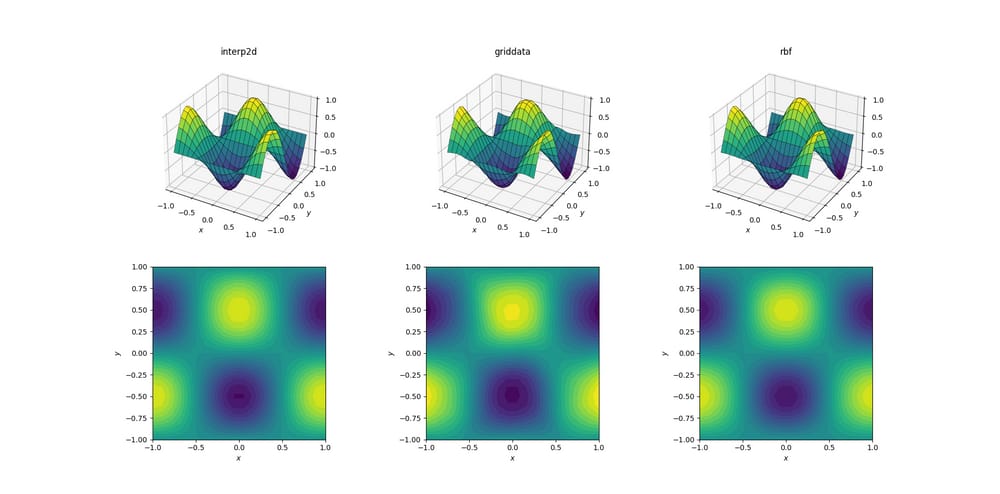
スムース関数とアップサンプリング

最も簡単なタスクから始めましょう。以下は、形状のメッシュからアップサンプリングする方法です。 [6, 7] のものにアップサンプリングする方法を示します。 [20, 21] は滑らかなテスト関数のために動作します。

これは単純な作業であるにもかかわらず、すでに出力には微妙な違いがあります。一見したところ、3つの出力はすべて妥当なものです。基礎となる関数の予備知識に基づいて、注目すべき 2 つの特徴があります: 中間のケースである griddata が最もデータを歪めている。なお y == -1 の境界(最も近い x ラベルに近い): 関数は厳密にゼロであるべきです (なぜなら y == -1 は滑らかな関数の結線だからです)、しかしこれは griddata . また x == -1 の境界(後ろ、左側)にも注目してください。下の関数は [-1, -0.5] に局所的な最大値（境界付近の勾配がゼロであることを意味する）を持ち、なおかつ griddata の出力はこの領域で明らかに非ゼロの勾配を示しています。その効果は微妙ですが、いずれにせよ偏りです。

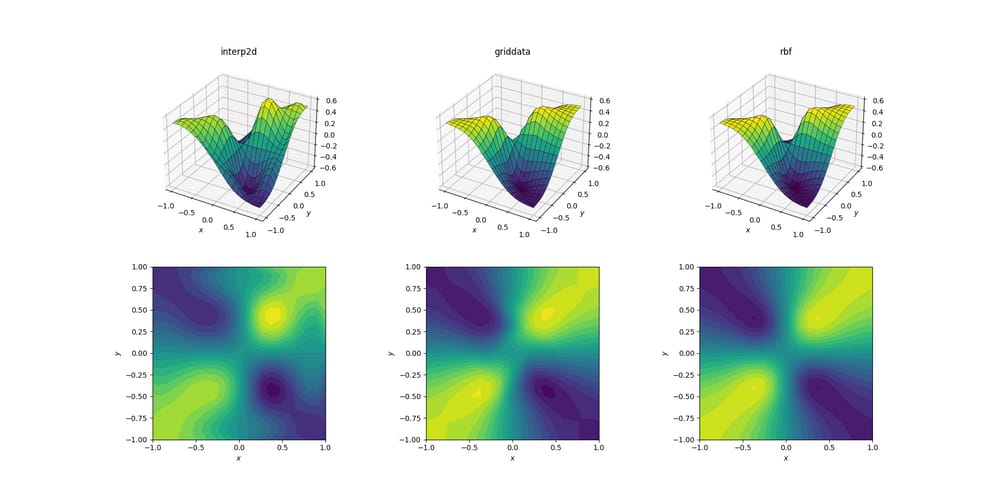
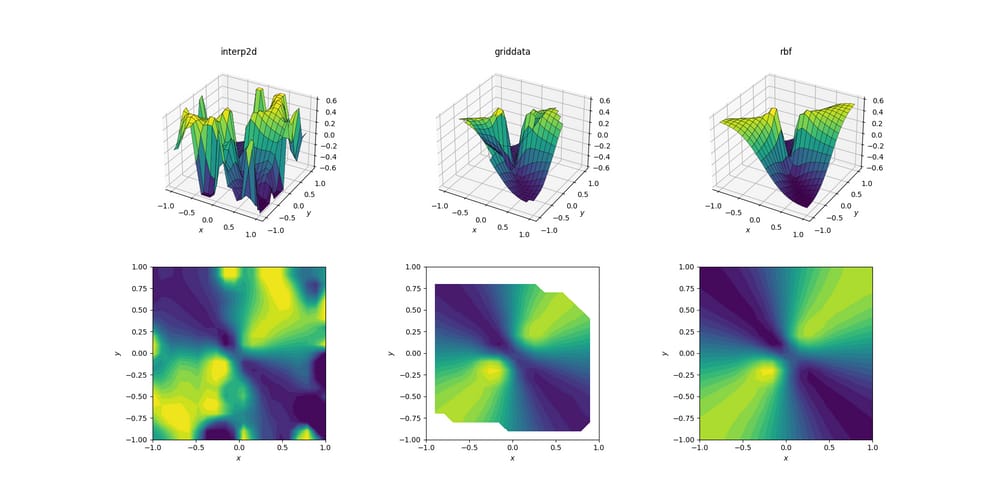
邪悪な関数とアップサンプリング

少し難しいタスクは、邪悪な関数にアップサンプリングを行うことです。

3つの手法の間に明確な違いが現れ始めています。サーフェスプロットをみると interp2d の出力に明らかな偽極値が現れています (プロットされた表面の右側にある 2 つのこぶに注目してください)。一方 griddata と RBFInterpolator の近くでローカルミニマムを生成し、一見したところ同じような結果を生むように見えます。 [0.4, -0.4] の近傍に局所極小値を生成するように見えますが、これは基本的な関数には存在しません。

しかし、1つの重要な側面があり、それは RBFInterpolator それは、基礎となる関数の対称性を尊重することです（もちろん、これはサンプルメッシュの対称性によっても可能になります）。の出力は griddata の出力はサンプル点の対称性を破りますが、これは滑らかなケースですでに弱く見えています。

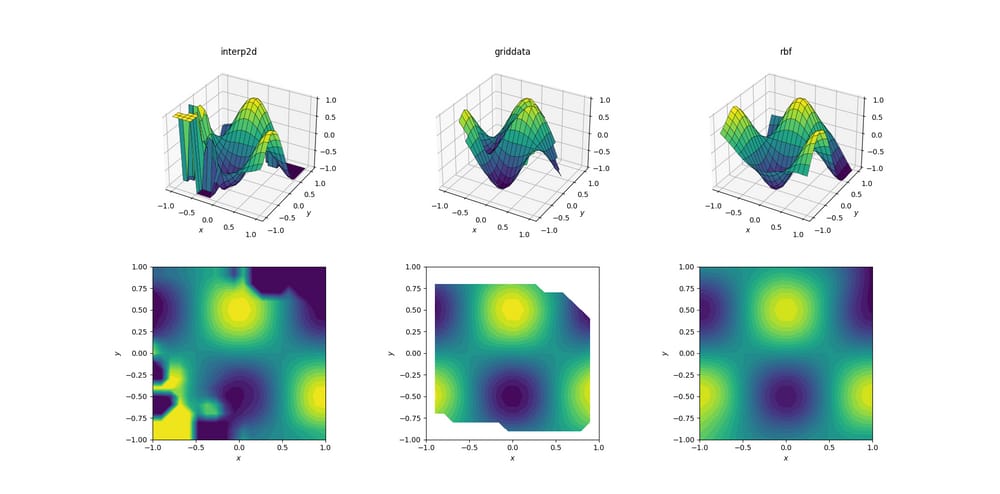
滑らかな関数と散布されたデータ

ほとんどの場合、散在したデータに対して補間を行いたいと思うものです。このため、これらのテストはより重要であると予想されます。上に示したように、サンプルポイントは関心のある領域で擬似的に一様に選ばれました。現実的なシナリオでは、各測定で追加のノイズが発生する可能性があり、そもそも生データを補間することに意味があるのかどうかを検討する必要があります。

スムース関数の出力です。

さて、すでにちょっとしたホラーショーが始まっています。からの出力を切り取って interp2d の間に [-1, 1] をプロット専用にすることで、少なくとも最小限の情報を保持することができます。根本的な形状は存在するものの、この方法が完全に破綻している巨大なノイズ領域が存在することは明らかです。2番目のケースは griddata の場合、形状はかなりきれいに再現されていますが、等高線プロットの境界部分に白い領域があることに注意してください。これは griddata が入力データ点の凸包内のみを処理するためです（言い換えれば、この処理では外挿 ). 凸包の外側にある出力点については、デフォルトの NaN 値を維持しました。 ² これらの特徴を考慮すると RBFInterpolator が一番性能が良いようです。

邪悪な機能と散在するデータ

そして、みんなが待ち望んでいた瞬間。

当然のことですが interp2d が諦めるのは大きな驚きではありません。実際、呼び出しの際に interp2d を呼び出している間は、フレンドリーな RuntimeWarning が表示され、スプラインの作成が不可能であることを訴えます。他の2つの方法については RBFInterpolator は、結果が外挿される領域の境界付近でさえも、最良の出力を生成するようです。

それでは、3つの方法について、好きな順に (最悪のものが誰にも読まれないように) 少し述べてみたいと思います。

`scipy.interpolate.RBFInterpolator`

の名前のRBFは RBFInterpolator クラスの名前のRBFはquot;radial basis functions"の略です。正直なところ、この記事のために調べ始めるまで、この方法を考えたことはありませんでしたが、将来的にこれを使うことは間違いないでしょう。

スプラインベースの手法（後述）と同様に、使用方法は2つのステップで行われます：まず、呼び出し可能な RBFInterpolator クラスのインスタンスを作成し、次に与えられた出力メッシュに対してこのオブジェクトを呼び出し、補間された結果を取得します。スムーズアップサンプリングテストの例です。

import scipy.interpolate as interp

sparse_points = np.stack([x_sparse.ravel(), y_sparse.ravel()], -1)  # shape (N, 2) in 2d
dense_points = np.stack([x_dense.ravel(), y_dense.ravel()], -1)  # shape (N, 2) in 2d

zfun_smooth_rbf = interp.RBFInterpolator(sparse_points, z_sparse_smooth.ravel(),
                                         smoothing=0, kernel='cubic')  # explicit default smoothing=0 for interpolation
z_dense_smooth_rbf = zfun_smooth_rbf(dense_points).reshape(x_dense.shape)  # not really a function, but a callable class instance

zfun_evil_rbf = interp.RBFInterpolator(sparse_points, z_sparse_evil.ravel(),
                                       smoothing=0, kernel='cubic')  # explicit default smoothing=0 for interpolation
z_dense_evil_rbf = zfun_evil_rbf(dense_points).reshape(x_dense.shape)  # not really a function, but a callable class instance

のAPIを作るために、配列の構築の工夫をしなければならないことに注意してください。 RBFInterpolator を満足させるために、いくつかの配列構築をしなければならないことに注意してください。2 次元点を形状の配列として渡さなければならないので (N, 2) の配列として渡す必要があるため、入力グリッドを平坦化し、平坦化された2つの配列をスタックする必要があります。構築されたインターポレータもこの形式のクエリーポイントを想定しており、その結果は 1 次元配列の形状 (N,) の配列となり、これをプロットするために 2 次元グリッドにマッチするように再形成しなければなりません。このため RBFInterpolator は入力点の次元数について仮定しないので、補間のために任意の次元をサポートします。

では scipy.interpolate.RBFInterpolator

おかしな入力データでもきちんとした出力が得られる。
高次元での補間をサポート
入力点の凸包の外側を外挿する（もちろん外挿は常にギャンブルであり、一般的には全く当てにしない方が良い）。
最初のステップとして補間器を作成するため、さまざまな出力ポイントでそれを評価することが少ない追加作業となります。
任意の形状の出力点配列を持つことができる（矩形メッシュに制約されるのとは対照的、後述）。
入力データの対称性を保持する可能性が高くなります。
キーワードのための複数の種類の放射状関数をサポート kernel : multiquadric , inverse_multiquadric , inverse_quadratic , gaussian , linear , cubic , quintic , thin_plate_spline (デフォルト)です。SciPy 1.7.0では、技術的な理由により、このクラスはカスタムの callable を渡すことができませんが、将来のバージョンで追加される可能性があります。
を大きくすることで、不正確な補間を行うことができます。 smoothing パラメーター

RBF補間の欠点として、補間する際に N を反転させる必要があることです。 N x N 行列の逆行列が発生する。この二次的な複雑さは、多数のデータポイントのために必要なメモリをあっという間に吹き飛ばしてしまう。しかし、新しい RBFInterpolator クラスは neighbors キーワードパラメータをサポートし、各放射線基底関数の計算を k に制限し、それによってメモリの必要性を減らします。

`scipy.interpolate.griddata`

以前のお気に入り。 griddata は任意の次元で補間を行うための一般的なワークホースです。これは、節点の凸包の外側の点に対して単一のプリセット値を設定する以上の外挿を実行しませんが、外挿は非常に気まぐれで危険なものなので、これは必ずしも悪いことではありません。使用例です。

sparse_points = np.stack([x_sparse.ravel(), y_sparse.ravel()], -1)  # shape (N, 2) in 2d
z_dense_smooth_griddata = interp.griddata(sparse_points, z_sparse_smooth.ravel(),
                                          (x_dense, y_dense), method='cubic')  # default method is linear

入力配列に対して，以下のように同じ配列変換が必要であることに注意してください． RBFInterpolator . 入力点は，形状が [N, D] で D 次元の配列、あるいは1次元の配列のタプルとして使用します。

z_dense_smooth_griddata = interp.griddata((x_sparse.ravel(), y_sparse.ravel()),
                                          z_sparse_smooth.ravel(), (x_dense, y_dense), method='cubic')

出力点の配列は、（上記の両方のスニペットのように）任意の次元の配列のタプルとして指定することができ、より柔軟性を持たせることができます。

簡単に言えば scipy.interpolate.griddata

おかしな入力データでもきちんとした出力が得られる。
高次元での補間をサポート
は外挿を行わないので、入力点の凸包の外側の出力に単一の値を設定することができます ( fill_value )
は一回の呼び出しで補間された値を計算するので、複数の出力点のセットをプローブすることはゼロから始まります。
任意の形状の出力ポイントを持つことができる
は、任意の次元での最近傍補間と線形補間、1次元と2次元の3次元補間をサポートしています。最近傍補間と線形補間では NearestNDInterpolator と LinearNDInterpolator をそれぞれ使用します。1 次元 3 次元補間はスプラインを使い、2 次元 3 次元補間は CloughTocher2DInterpolator を使用して連続微分可能な区分的三次補間器を構成します。
は入力データの対称性に違反する可能性があります。

`scipy.interpolate.interp2d` / `scipy.interpolate.bisplrep`

私が議論している唯一の理由は interp2d とその親類について説明する唯一の理由は、それがまやかしの名前を持っていて、人々がそれを使ってみようとしそうだからです。ネタバレ注意：使ってはいけません（scipyバージョン1.7.0現在）。特に2次元の補間に使われるという点で、すでにこれまでの科目よりも特殊ですが、多変量補間の場合は圧倒的にこちらの方が多いのではないでしょうか。

構文としては interp2d と似ています。 RBFInterpolator と似ていて、最初に補間インスタンスを作成する必要があり、そのインスタンスが実際の補間値を提供するために呼び出されるようになっています。しかし、出力点は矩形メッシュ上に配置されなければならないので、補間器への呼び出しへの入力は出力グリッドにまたがる1次元ベクトルでなければならず、あたかも numpy.meshgrid :

# reminder: x_sparse and y_sparse are of shape [6, 7] from numpy.meshgrid
zfun_smooth_interp2d = interp.interp2d(x_sparse, y_sparse, z_sparse_smooth, kind='cubic')   # default kind is 'linear'
# reminder: x_dense and y_dense are of shape (20, 21) from numpy.meshgrid
xvec = x_dense[0,:] # 1d array of unique x values, 20 elements
yvec = y_dense[:,0] # 1d array of unique y values, 21 elements
z_dense_smooth_interp2d = zfun_smooth_interp2d(xvec, yvec)   # output is (20, 21)-shaped array

を使用する際の最も一般的な間違いのひとつは interp2d を使用する際の最も一般的な間違いは、2次元のフルメッシュを補間呼び出しに入れることであり、これはメモリの爆発的な消費につながり、できれば急いで MemoryError .

さて、最大の問題点である interp2d の最大の問題は、それがしばしば機能しないことです。これを理解するためには、フードの下を覗かなければなりません。その結果 interp2d は低レベル関数のラッパーであり bisplrep + bisplev これらは、FITPACK ルーチン（Fortran で書かれています）のラッパーです。前の例と同等の呼び出しは次のようになります。

kind = 'cubic'
if kind == 'linear':
    kx = ky = 1
elif kind == 'cubic':
    kx = ky = 3
elif kind == 'quintic':
    kx = ky = 5
# bisplrep constructs a spline representation, bisplev evaluates the spline at given points
bisp_smooth = interp.bisplrep(x_sparse.ravel(), y_sparse.ravel(),
                              z_sparse_smooth.ravel(), kx=kx, ky=ky, s=0)
z_dense_smooth_bisplrep = interp.bisplev(xvec, yvec, bisp_smooth).T  # note the transpose

さて、ここで interp2d : (scipy version 1.7.0では) 素晴らしいのコメントがあります。 interpolate/interpolate.py に対して interp2d :

if not rectangular_grid:
    # TODO: surfit is really not meant for interpolation!
    self.tck = fitpack.bisplrep(x, y, z, kx=kx, ky=ky, s=0.0)

であり、実際に interpolate/fitpack.py では bisplrep にはいくつかの設定があり、最終的には

tx, ty, c, o = _fitpack._surfit(x, y, z, w, xb, xe, yb, ye, kx, ky,
                                task, s, eps, tx, ty, nxest, nyest,
                                wrk, lwrk1, lwrk2)

で、終わりです。の下にあるルーチンは interp2d の下にあるルーチンは、実際には補間を行うためのものではありません。十分に行儀の良いデータであれば十分かもしれませんが、現実的な環境ではおそらく他のものを使いたいでしょう。

結論から言うと interpolate.interp2d

よく調整されたデータであってもアーティファクトにつながる可能性があります。
は二変量問題に特化したものです（ただし、限定された interpn はグリッド上で定義された入力点に対するものです)
外挿を行う
最初のステップとして補間器を作成するので、さまざまな出力ポイントで評価することができ、追加的な労力が少なくて済む
は矩形グリッド上の出力しか生成できないので、散乱した出力にはループでインターポレータを呼び出す必要がある。
線形、三次、五次補間をサポートしています。
入力データの対称性に違反する可能性がある

¹ かなり確かなのは cubic と linear の基底関数の種類は RBFInterpolator は他の同名のインターポレータと正確に対応していません。

² matplotlibは歴史的に、適切な深度情報を持つ複雑な3Dオブジェクトの描画に困難を抱えています。データ中の NaN 値はレンダラーを混乱させるので、表面の奥にあるべき部分が手前にプロットされてしまいます。これは視覚化の問題であり、補間の問題ではありません。