BinaryDevelop
  1. ホーム
  2. python

scipy 科学技術計算

2022-02-09 08:37:15

Scipy ハイエンド科学計算

アドリアン・ショーヴ、アンドレ・エスパゼ、エマニュエル・グイヤール、ガエル・ヴァロコー、ラルフ・ゴマーズ著

Translated from. scipy講義ノート

翻訳者曰く、最後の部分がよくわからない、このドキュメントはメンテナンス中です・・・とのこと。

<スパン サイピー

scipy パッケージは、科学計算における一般的な問題に特化した様々なツールキットを含んでいます。その異なるサブモジュールは、異なるアプリケーションに対応しています。例えば、補間、統合、最適化、画像処理、特殊関数、等々です。

scipyはGSL (GNU C or C++ Scientific Computing Library)やMatlab toolboxのような他の標準的な科学計算ライブラリと比較することができます。 scipyはPythonの科学計算プログラムのコアパッケージで、numpy行列を効率的に計算し、numpyとscipyを一緒に動作させるために使用されています。

プログラムを実装する前に、必要なデータ処理がすでにscipyに備わっているかどうかを確認しておくとよいでしょう。専門家ではないプログラマーとして、科学者は常に を構築するための車輪の再発明 その結果、バグが多く、最適化されていない、共有やメンテナンスが困難なコードになってしまいます。それに対して、Scipyのプログラムは最適化され、テストされているので、可能な限り使用する必要があります。

目次

ご注意 このチュートリアルは数値計算の本当の入門にはほど遠いものです。scipyの様々なサブモジュールや関数を列挙することはとても退屈なので、代わりにいくつかの例に集中して、`scipy`をどのように計算に使用するかについての一般的な考えを提供することにします。

scipy はいくつかの関数に特化したサブモジュールから構成されています。

<テーブル モジュール 機能 scipy.cluster ベクトル量子化／K-means scipy.constants（定数 物理・数学定数 scipy.fftpack フーリエ変換 scipy.integrate 積分プログラム scipy.interpolate 内挿分割 scipy.io データの入出力 scipy.linalg 線形代数プログラム scipy.ndimage n 次元画像パッケージ scipy.odr 直交距離回帰 scipy.optimize 最適化 scipy.シグナル 信号処理 scipy.sparse スパース行列 scipy.spatial 空間データ構造およびアルゴリズム scipy.special 任意の特殊な数学関数 scipy.stats 統計情報

これらはすべて numpy しかし、それぞれはほとんど独立しています。Numpyとこれらのscipyモジュールをインポートする標準的な方法は次のとおりです。 

import numpy as np
from scipy import stats # Other submodules are the same

メイン scipy 名前空間のほとんどは、本当のnumpyの関数を含んでいます（np.cosであるscipy.cosを試してみてください）。これらは歴史的な理由のために存在するだけで、通常、名前空間を使用する理由はありません。 

import scipy

ファイル入出力：scipy.io

  • matlabファイルのインポートと保存。 

      In [1]: from scipy import io as spio
    
  In [3]: import numpy as np
    
  In [4]: a = np.ones((3, 3))
    
  In [5]: spio.savemat('file.mat', {'a': a}) # savemat expects a dictionary
  /usr/lib/python2.7/site-packages/scipy/io/matlab/mio.py:266: FutureWarning: Using oned_as default value ('column') This will change to 'row' in future versions
    oned_as=oned_as)
    
  In [6]: data = spio.loadmat('file.mat', struct_as_record=True)
    
  In [7]: data['a']
  Out[7]: 
  array([ 1., 1., 1.],
         [ 1., 1., 1.],
         [ 1., 1., 1.]])

  • 画像を読み込むため。 

      In [16]: from scipy import misc
    
  In [17]: misc.imread('scikit.png')
  Out[17]: 
  array([[[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]],
    
         [[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]],
    
         [[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]],
    
         ... , 
         [[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]],
    
         [[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]],
    
         [[255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          ... , 
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255],
          [255, 255, 255, 255, 255]], dtype=uint8)
    
  In [18]: import matplotlib.pyplot as plt
    
  In [19]: plt.imread('scikit.png')
  Out[19]: 
  array([[ 1., 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          ... , 
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.]],
    
         [[ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          ... , 
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.]],
    
         [[ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          ... , 
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.]],
    
         ... , 
         [[ 1., 1., 1., 1.],
          [ 1., 1., 1., 1.],
          [ 1

こちらもご覧ください。

  • txtファイルの読み込み：numpy.loadtxt()/numpy.savetxt()
  • テキスト/CSVファイルのスマートなインポート：numpy.genfromtxt()/numpy.recfromcsv()
  • 高速で効率的だがnumpy特有のバイナリフォーマット：numpy.save()/numpy.load()

特殊関数：scipy.special

特殊関数は、アプリオリな関数です。 scipy.special のドキュメント文字列は非常によく書かれているので、ここではすべての関数をリストアップすることはしません。よく使われるものは

  • ベッセル関数、例えば scipy.special.jn() (整数n次ベッセル関数)
  • 楕円関数( scipy.special.ellipj() ヤコビ楕円関数、......)
  • ガンマ関数 scipy.special.gamma() ということに注意し、また scipy.special.gammaln この関数はガンマ関数を対数座標で与えるので、数値の精度が高くなります。

線形代数演算：scipy.linalg

scipy.linalg モジュールは、基礎となる効率的な実装 (BLAS, LAPACK) に依存して、標準的な線形代数演算を提供します。

  • scipy.linalg.det() 正方行列の行列式を計算する関数です。 

      In [22]: from scipy import linalg
    
  In [23]: arr = np.array([[1, 2],
     .... : [3, 4]])
    
  In [24]: linalg.det(arr)
  Out[24]: -2.0
    
  In [25]: linalg.det(np.ones((3,4)))
  ---------------------------------------------------------------------------
  ValueError Traceback (most recent call last)
  <ipython-input-25-375ad1d49940> in <module>()
  ----> 1 linalg.det(np.ones((3,4)))
    
  /usr/lib/python2.7/site-packages/scipy/linalg/basic.pyc in det(a, overwrite_a)
      398 a1 = np.asarray_chkfinite(a)
      399 if len(a1.shape) ! = 2 or a1.shape[0] ! = a1.shape[1]:
  --> 400 raise ValueError('expected square matrix')
      401 overwrite_a = overwrite_a or _datacopied(a1, a)
      402 fdet, = get_flinalg_funcs(('det',), (a1,))
    
  ValueError: expected square matrix

py.linalg.inv()` 関数は、正方行列の逆行列を計算します。 

    In [26]: arr = np.array([[1, 2],
                    [3, 4]])
    
    In [27]: iarr = linalg.inv(arr)
    
    In [28]: iarr
    Out[28]: 
    array([[-2. , 1. ],
           [ 1.5, -0.5]])
    
    In [29]: np.allclose(np.dot(arr, iarr), np.eye(2))
    Out[29]: True

最後に特異配列の逆行列（行列式0を持つ）を計算すると、次のようになります（raise）。 LinAlgError : 

    In [32]: arr = np.array([[3, 2],
                    [6, 4]])
    
    In [33]: linalg.inv(arr)
    ---------------------------------------------------------------------------
    LinAlgError Traceback (most recent call last)
    <ipython-input-33-52c04c854a80> in <module>()
    ----> 1 linalg.inv(arr)
    
    /usr/lib/python2.7/site-packages/scipy/linalg/basic.pyc in inv(a, overwrite_a)
        346 inv_a, info = getri(lu, piv, overwrite_lu=1)
        347 if info > 0:
    --> 348 raise LinAlgError("singular matrix")
        349 if info < 0:
        350 raise ValueError('illegal value in %d-th argument of internal '
    
    LinAlgError: singular matrix

  • さらに高度な操作として、特異値分解（SVD）などがあります。 

    In [34]: arr = np.range(9).reshape((3, 3)) + np.diag([1, 0, 1])
    
In [35]: uarr, spec, vharr = linalg.svd(arr)

    その結果、配列スペクトルは 

    In [36]: spec
Out[36]: array([ 14.88982544, 0.45294236, 0.29654967])

    元の行列は、svd の出力に np.dot ドットプロダクトを再結合して得られる。 

    In [37]: sarr = np.diag(spec)
    
In [38]: svd_mat = uarr.dot(sarr).dot(vharr)
    
In [39]: np.allclose(svd_mat, arr)
Out[39]: True

SVDは信号処理や統計学で広く使われている。他の多くの標準的な分解（QR、LU、コレスキー、シューア）や線形系の解も scipy.linalg で

高速フーリエ変換: scipy.fftpack

scipy.fftpack モジュールは、高速フーリエ変換を計算するために使用されます。例として、（ノイズの多い）入力信号は次のようになります。 

  In [40]: time_step = 0.02
  
  In [41]: period = 5
  
  In [42]: time_vec = np.range(0, 20, time_step)
  
  In [43]: sig = np.sin(2 * np.pi / period * time_vec) + \
     .... : 0.5 * np.random.randn(time_vec.size)

観測者は、信号の周波数ではなく、等間隔にサンプリングされた信号のシグネチャをガイドします。信号は実関数から来るはずなので、フーリエ変換は対称になります。 scipy.fftpack.fftfreq() 関数がサンプリング周波数を生成し scipy.fftpack.fft() の高速フーリエ変換を計算します。

パワーの結果は対称的なので、周波数を求めるにはスペクトルの正の部分のみを使用する必要があります。 

  In [48]: pidxs = np.where(sample_freq > 0)
  
  In [49]: freqs = sample_freq[pidxs]
  
  In [50]: power = np.abs(sig_fft)[pidxs]

信号の周波数はこのように求めることができます。 

  In [51]: freq = freqs[power.argmax()]
  
  In [52]: np.allclose(freq, 1./period)
  Out[52]: True

これでフーリエ変換された信号から高周波のノイズが除去されることになります。 

  In [53]: sig_fft[np.abs(sample_freq) > freq] = 0

フィルタリングされた信号を得るには scipy.fftpack.ifft 関数で計算します。 

  In [54]: main_sig = fftpack.ifft(sig_fft)

その結果を可視化すると、次のようになります。 

  In [55]: plt.figure()
  Out [55]: <matplotlib.figure.Figure at 0x4a9fb50>
  
  In [56]: plt.plot(time_vec, sig)
  Out [56]: [<matplotlib.lines.Line2D at 0x4ad3790>]
  
  In [57]: plt.plot(time_vec, main_sig, linewidth=3)
  /usr/lib/python2.7/site-packages/numpy/core/numeric.py:320: ComplexWarning: Casting complex values to real discards the imaginary part
    return array(a, dtype, copy=False, order=order)
  Out [57]: [<matplotlib.lines.Line2D at 0x4ad3dd0>]
  
  In [58]: plt.xlabel('Time [s]')
  Out [58]: <matplotlib.text.Text at 0x4aad050>
  
  In [59]: plt.ylabel('Amplitude')
  Out [59]: <matplotlib.text.Text at 0x4aadbd0>
  
  In [60]: plt.show()

numpy.fft

NumpyにもFFTの実装があります(numpy.fft)。しかし、scipyの方がより効率的な実装を使用しているので、通常はscipyの方を優先して使用すべきです。

作業例：元のサイクルを見つける

ソースコード

ソースコード

作業例です。ガウシアン画像ぼかし

コンボリューション

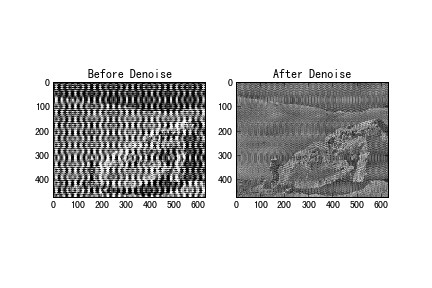
<スパン <スパン <スパン <スパン <スパン <スパン f <スパン <スパン 1 <スパン ( t ) <スパン = ∫ d <スパン <スパン t <スパン <スパン ′ K ( t <スパン - <スパン <スパン <スパン <スパン t <スパン <スパン ′ ) <スパン <スパン f <スパン <スパン 0 <スパン ( <スパン t <スパン <スパン ′ )
<スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン <スパン f <スパン <スパン 1 <スパン ~ ( ω ) = <スパン <スパン <スパン <スパン K ~ ( ω ) <スパン <スパン <スパン <スパン <スパン <スパン f <スパン <スパン 0 <スパン ~ ( ω )

演習を行う。月面着陸画像のノイズ除去

  1. 提供された画像moonlanding.pngを調べると、周期的なノイズで大きく汚染されていることがわかります。この演習では、高速フーリエ変換を使用してノイズを除去することを目指します。
  2. を使用します。 plt.imread で画像を読み込む。
  3. を使用します。 scipy.fftpack の2次元フーリエ関数で、画像のスペクトル線（フーリエ変換）を求め、プロットすることができます。このスペクトル線を可視化することは問題ないでしょうか？もしそうなら、それはなぜですか？
  4. このスペクトルには高周波成分と低周波成分が含まれています。ノイズは高周波部分にあるので、いくつかの成分を0にします（配列スライシングを使用）。
  5. 逆フーリエ変換を適用して、最終的な画像をご覧ください。

最適化および適合：scipy.optimize

最適化とは、方程式の最小値や数値解を求める問題である。

scipy.optimization このサブモジュールは、関数の最小化（スカラーまたは多次元）、カーブフィット、方程式の根を求めるための便利なアルゴリズムを提供します。 

from scipy import optimize

スカラー関数の最小値を求めよ

次のような関数を定義してみましょう。 

In [2]: def f(x):
   ... : return x**2 + 10 * np.sin(x)

次にプロットします。 

In [3]: x = np.range(-10, 10, 0.1)

In [4]: plt.plot(x, f(x))
Out [4]: [<matplotlib.lines.Line2D at 0x3e2a4d0>]

In [5]: plt.show()

<イグ

この関数は、約-1.3でグローバルミニマム、3.8でローカルミニマムを持つ。

この関数の最小値を求める一般的かつ効率的な方法は、初期点からの勾配降下法を用いることです。 1 は、次のような方法です。 

In [6]: optimize.fmin_bfgs(f, 0)
Optimization terminated successfully.
         Current function value: -7.945823
         Iterations: 5
         Function evaluations: 24
         Gradient evaluations: 8
Out[6]: array([-1.30644003])

この方法の問題点として、関数がローカルミニマムを持つ場合、アルゴリズムは初期点によってグローバルミニマムではなく、これらのローカルミニマムを見つけることになることが考えられる。 

In [7]: optimize.fmin_bfgs(f, 3, disp=0)
Out[7]: array([ 3.83746663])

初期点を選択するためにグローバルミニマムの近傍がわからない場合、よりリソースを消費する大域的最適化に頼る必要があります。グローバルミニマムを求めるには、最も単純なアルゴリズムとしてブルートフォースアルゴリズムがあります 2 このアルゴリズムは、与えられた格子点に対する各関数の値を求めるものである。 

In [10]: grid = (-10, 10, 0.1)

In [11]: xmin_global = optimize.brute(f, (grid,))

In [12]: xmin_global
Out[12]: array([-1.30641113])

より大きな格子点では scipy.optimize.brute() は非常に遅くなります。 scipy.optimize.aneal() シミュレーテッドアニーリングを用いた代替関数が提供されています。より効率的なアルゴリズムは、既知の大域的最適化問題の様々なクラスに対して存在しますが、これはscipyの範囲を超えています。いくつかの有用な大域的最適化パッケージは オープンオプト , IPOPT , PyGMO および PyEvolve .

ローカルミニマムを求めるために、変数を以下のように制限します。 (0, 10) との間に scipy.optimize.fminbound() : 

In [13]: xmin_local = optimize.fminbound(f, 0, 10)

In [14]: xmin_local
Out[14]: 3.8374671194983834

注意事項 アドバンストセクションで 数学的最適化：関数の最小値を求める は、関数の最小値を求めることについて、より詳しく説明しています。

<スパン スカラー関数の根を求める

ルートを求めるには、例えば f(x)=0 は、上記の例で使用した関数の場合、点 f を使用することができます。 scipy.optimize.fsolve() : 

In [17]: root = optimize.fsolve(f, 1) # Our initial guess is 1

In [18]: root
Out[18]: array([ 0.])

ルートは1つしか見つかっていないことに注意してください。fの画像が-2.5付近で2番目の根を持っていることを確認してください。この正確な値は、最初の推測を次のように調整することで見つけることができます。 

In [19]: root = optimize.fsolve(f, -2.5)

In [20]: root
Out[20]: array([-2.47948183])

<スパン カーブフィッティング

ノイズに汚染されたf値からサンプリングしたデータがあるとします。 

In [21]: xdata = np.linspace(-10, 10, num=20)

In [22]: ydata = f(xdata) + np.random.randn(xdata.size)

関数形式がわかっていれば（今の場合は x^2 + sin(x) )であるが、大きさがわからない。最小二乗法でフィットさせることで大きさを求めることができます。まず、フィットに使用する関数を定義します。 

In [23]: def f2(x, a, b):
   .... : return a*x**2 + b*np.sin(x)

次に scipy.optimize.curve_fit() を使って、aとbを求めます。 

In [24]: guess = [2, 2]

In [25]: params, params_covariance = optimize.curve_fit(f2, xdata, ydata, guess)

In [26]: params
Out[26]: array([ 1.00439471, 10.

関連

最新

おすすめ

について
/
プライバシー・ポリシー
/
お問い合わせ
© 2022 BinaryDevelop. すべての権利は、それぞれの所有者に帰属します