[解決済み] Python/SciPy用ピークファインディングアルゴリズム

質問

一次導関数のゼロクロスを求めるとかで、自分で何か書けそうですが、標準ライブラリに含まれているような一般的な関数のような気がします。 どなたかご存じないでしょうか？

私の特殊な用途は2次元配列ですが、通常はFFTのピークを見つけることなどに使われると思います。

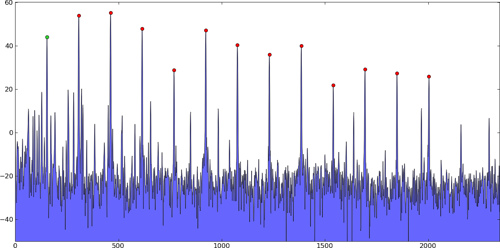
具体的には、この手の問題では、強いピークが複数あり、さらに無視すべきノイズによる小さなピークがたくさんあるのです。 これはあくまで例であり、私の実際のデータではありません。

1次元のピーク。

2次元のピーク。

ピーク検出アルゴリズムは、これらのピークの位置（値だけでなく）を見つけ、理想的には、最大値を持つインデックスだけでなく、真のサンプル間ピークを見つけるために、おそらく次のような方法を使用します。 二次補間 などがあります。

一般的には、いくつかの強いピークにしか関心がないので、ある閾値を超えたから選ばれるか、あるいは、最初の n のピークを振幅の順に並べたものである。

言ったように、私は自分でこのようなものを書く方法を知っています。 ただ、うまく機能することが知られている既存の関数やパッケージがあるかどうかを尋ねているだけです。

更新してください。

I MATLABスクリプトの翻訳 1次元の場合はうまくいくのですが、もっとうまくいくかもしれません。

アップデートを更新しました。

シクステンベ より良いバージョンを作成しました。 は、1次元の場合です。

解決方法は？

機能 scipy.signal.find_peaks は、その名前が示すように、このような場合に便利です。しかし、そのパラメータをよく理解することが重要です。 width , threshold , distance そしてなによりも prominence を使用することで、良好なピーク抽出を行うことができます。

私のテストとドキュメントによると、このコンセプトは プロミネンス は、良いピークを残し、ノイズの多いピークを捨てるために有用な概念"である。

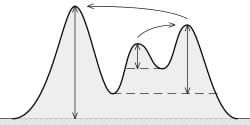
とは (地形的な）プロミネンス ? それは 山頂からより高い地形に行くために、降下するのに必要な最低の高さです。 このように。

という考えです。

目立つほど、そのピークが重要であることを意味します。

テストします。

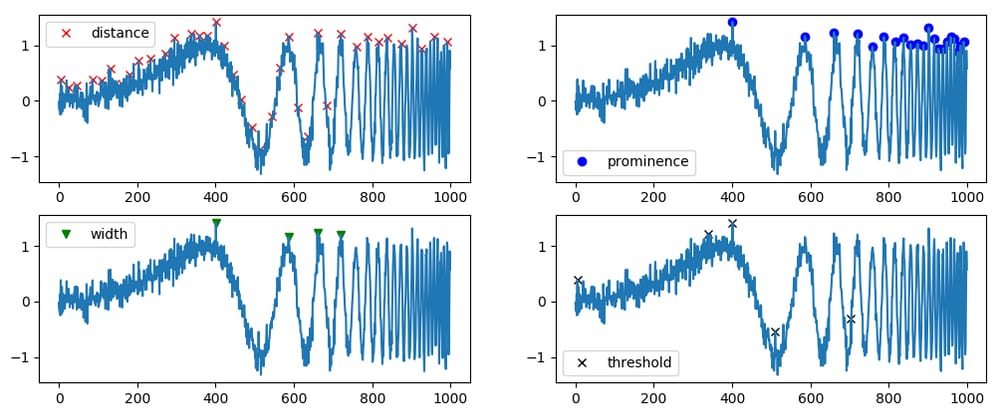
周波数が変化する正弦波は、いろいろと難しいことがわかるので、あえて（ノイズの多い）正弦波を使いました。このように width パラメータはあまり役に立ちません。 width が高すぎると、高域の非常に近いピークを追えなくなる。もし width 低すぎると、信号の左側部分に不要なピークがたくさんできてしまいます。同じ問題で distance . threshold は直接の近傍としか比較しないので、ここでは役に立ちません。 prominence が最適解を与えるものです。なお、これらのパラメータはいくつでも組み合わせることができます!

コード

import numpy as np
import matplotlib.pyplot as plt 
from scipy.signal import find_peaks

x = np.sin(2*np.pi*(2**np.linspace(2,10,1000))*np.arange(1000)/48000) + np.random.normal(0, 1, 1000) * 0.15
peaks, _ = find_peaks(x, distance=20)
peaks2, _ = find_peaks(x, prominence=1)      # BEST!
peaks3, _ = find_peaks(x, width=20)
peaks4, _ = find_peaks(x, threshold=0.4)     # Required vertical distance to its direct neighbouring samples, pretty useless
plt.subplot(2, 2, 1)
plt.plot(peaks, x[peaks], "xr"); plt.plot(x); plt.legend(['distance'])
plt.subplot(2, 2, 2)
plt.plot(peaks2, x[peaks2], "ob"); plt.plot(x); plt.legend(['prominence'])
plt.subplot(2, 2, 3)
plt.plot(peaks3, x[peaks3], "vg"); plt.plot(x); plt.legend(['width'])
plt.subplot(2, 2, 4)
plt.plot(peaks4, x[peaks4], "xk"); plt.plot(x); plt.legend(['threshold'])
plt.show()