Pythonによるクラスタ分析のためのK-meansアルゴリズムの実装の詳細プロセス

K-meansアルゴリズムの紹介

  K-meansアルゴリズムは、距離を類似性の評価指標とする、つまり、2つの物体が近いほど類似性が高いと考えられる、非常に典型的な距離ベースのクラスタリングアルゴリズムである。このアルゴリズムでは、距離の近い物体からクラスタが構成されると考えるため、コンパクトで独立したクラスタを得ることを最終的な目標としている。

アルゴリズムの処理は以下の通りです。

1) N個の文書からランダムにK個の文書をセントロイドとして選択する。

2) 残りの各文書について、各重心までの距離を測定し、最も近い重心のクラスに割り当てる。

3) 既に得られている各クラスのセントロイドを再計算する。

4) 新しい重心が元の重心と等しいか、指定した閾値より小さくなるまで2～3ステップ繰り返し、アルゴリズムが終了する。

アルゴリズムの長所と短所。

長所

• 原理的にシンプル
• 高速
• 大規模データに対する優れたスケーラビリティ

デメリット

• クラスタ数Kを指定する必要がある
• 外れ値に敏感
• 初期値感応型コードの実装。

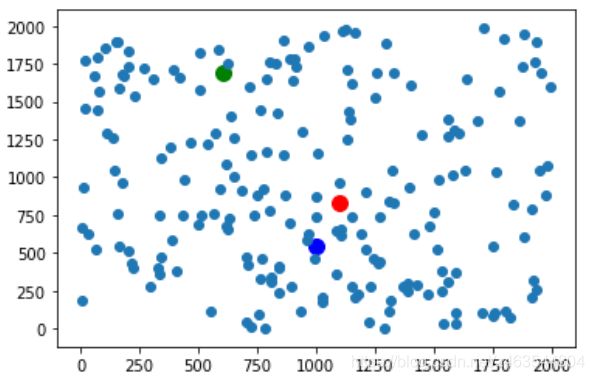
まず、ランダムに200点を生成し、その間の(0,2000)を取って素数の数を決定します。ここでは3の素数を取り、これもランダムに生成します（需要に応じて変更可能です）。

｛
	"records":[
				{
					...
					"id" = "123",
					"state" = 1,
					...
				},
				{
					...
					"id" = "456",
					"state" = 0,
					...
				}
				{
					...
					"id" = "789",
					"state" = 0,
					...
				}
]
}

        結果は次のようになります。

次に、numpy をインポートして、各点と重心との距離を計算し、重心からの距離に応じて各点をソートし、最初の点に近ければリストの最初の位置に、2番目に近ければ2番目の位置に、といった具合に割り当てます。

$.records[? (@.state==0)].id

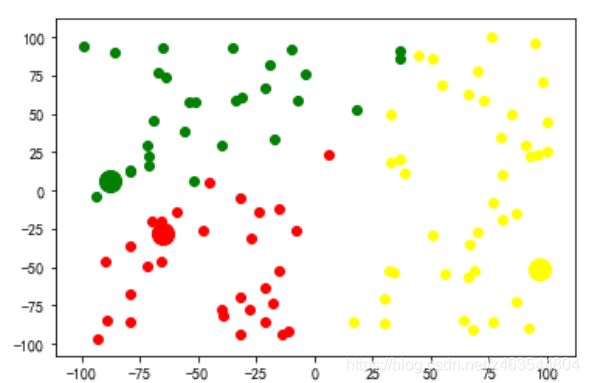
ご覧のように、200の点が3つの重心からの距離に基づいて3つに分類され、3つの重心それぞれに割り当てられた点の位置を含むリストがグループ内に3つ存在します。これを可視化してループに追加し、反復して比較的最適な重心を見つけるには、次のコードを実行します。

[
	"456", "789"
]

  ここでは合計10回の反復を設定していますが、このように8回目の反復で最適な重心を発見していることが分かります。

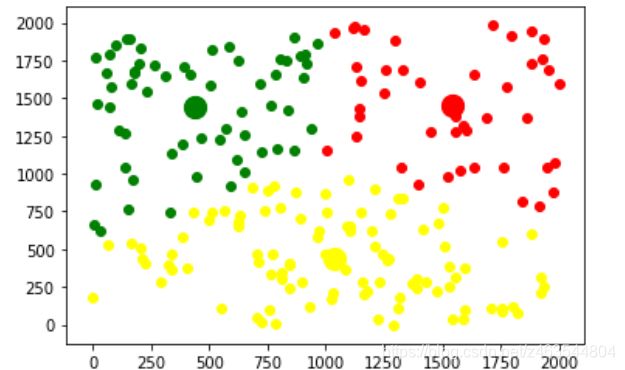
以上、k-meansアルゴリズムの簡単な実装を紹介しましたが、何か質問があれば、遠慮なくコメントを残してください。

pythonを使ったクラスタリング分析 - K-meansの記事は以上となります。pythonのK-meansクラスタリング分析については、Script Houseの過去記事を検索するか、引き続き以下の関連記事を閲覧してください。