Python ツリー選択ソート(Selection Sorting)機能

1. 導入

選択ソートには大きく分けて、単純選択ソート、木選択ソート、ヒープソートの3つのソートがあります。今日の記事では、ツリー選択ソートに焦点を当て、ツリー選択ソートはまた、トーナメントソートとして知られている、ツリー選択ソートは、キーワードのn個のレコードの最初の2つの比較を参照し、トーナメントソートのアイデアを使用し、その後に n/2 というように、最小のレコードが選択されるまで続けます。

2. 問題の説明

ある配列が与えられたとき、木選択ソートを使ってどのように並べ替えるか、図と文章で以下に説明する。

例1：データテーブルA＝（73、45、79、90、81、75、94、97）をソートする場合

出力する。45 73 75 79 81 90 94 97

3. 解決方法

データテーブルAは無秩序であり、今、それは最初の葉としてすべてのレコードを比較する必要がある木選択ソートの考え方によると、最小から最大への順序でソートする必要があり、次に左から右へ順番に、2つの比較によって、最小の1つを選択し、その後再び左から右へ順序でn / 2要素の比較、2つの比較によって、最小を選択して、この操作後に繰り返されています、意志 この操作を繰り返し後に、下から上に完全な二項木が形成されています。この段落を読んでもなかなか理解できないかもしれないので、以下に図で説明することにする。

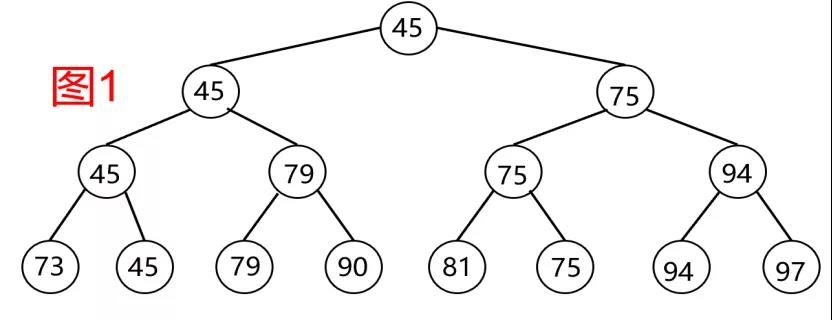
1. バイナリーツリーを構築する。 図1は、データテーブルAで構成されるバイナリツリー、最初に直接下部にあるデータテーブルAのデータ、つまり、バイナリツリーの葉で、次に左から右へ2つずつ比較するために、例えば、73と45を比較した後に最小の45、79と90を比較した後に、最小の45を比較する45と79が選択されますが、このように完全バイナリツリーの組成まで繰り返されている。

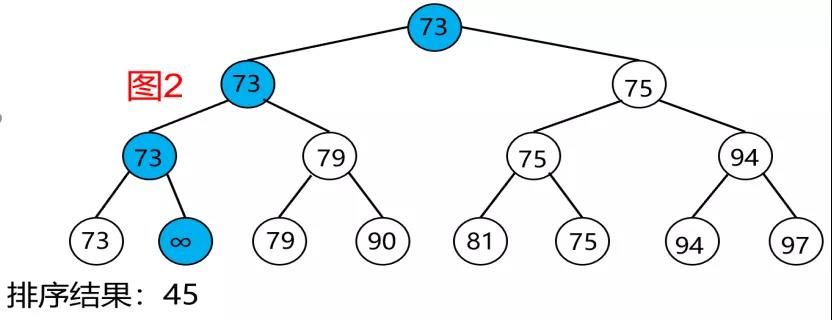
2. 正しい順序で出力する方法。 図1によれば、ルートノードは45であり、これが最小であることがわかります。図2は、ルートノードが最小になるまで、図1と図2の比較を通じて、最小を見つけるために、最初の時間で見ることができる無限記号で置き換え45を見つけるために、次に2つずつ比較され45、2回目は73ですが、今では無限記号で置き換え73を見つけ、順序ですべてのデータまで、上記の操作を繰り返す。次の図は、次のとおりです。

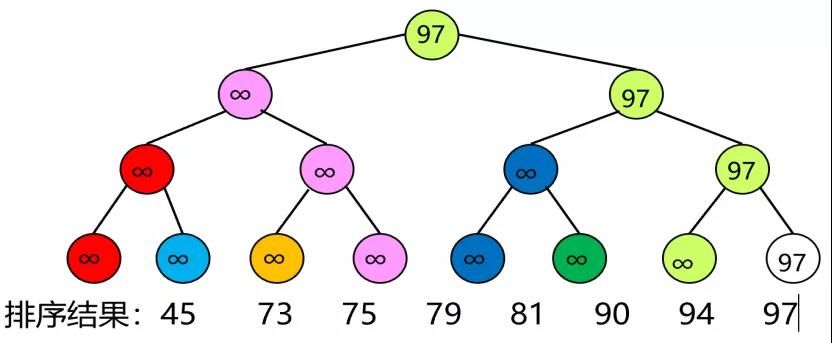
4. 結論

ツリー選択ソートはまだ比較的理解されており、グラフとテキストの組み合わせはより簡単です。

Pythonの選択ソートにおけるツリー選択についての記事は以上となります。Pythonの木選択ソートについては、Scripting Houseの過去記事を検索していただくか、引き続き以下の関連記事をご覧ください。