[解決済み] ロジスティック回帰のpythonソルバーの定義
質問
sklearnのロジスティック回帰関数を使っているのですが、最適化問題を解くために、それぞれのソルバーが裏で実際に何をしているのか気になります。
どなたか、"newton-cg", "sag", "lbfgs" と "liblinear" が何をしているのかを簡単に説明していただけませんか。
どのように解決するのですか?
さて、パーティに遅刻していなければいいのですが......。まずは、たくさんの情報を掘り下げる前に、直感を確立することを試みてみましょう ( 注意 これは簡単な比較ではありません。 TL;DR)
はじめに
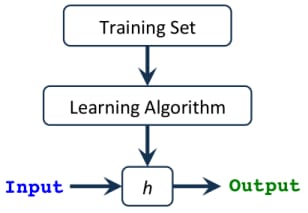
仮説
h(x)
は
入力
を受け取り
推定出力値
.
この仮説は1変数の連立方程式のような単純なものから、使っているアルゴリズムの種類によっては非常に複雑で長い多変数方程式まであります( 例:線形回帰、ロジスティック回帰...etc. ).
私たちのタスクは 最適なパラメータ (シータやウェイトなど)を使って 最小の誤差 を計算し、出力を予測する。この誤差を計算する関数を コストまたは損失関数 であり、どうやら私たちの目標は を最小化することです。 を最小化し、最良の予測出力を得ることができます。
もう一つ思い出してほしいのは、パラメータ値とコスト関数への影響(つまり誤差)の関係は、次のようになります。 ベル曲線 (すなわち 二次曲線 重要なので思い出してください).
そこで、その曲線の任意の点から始めて、止まった各点の微分(つまり接線)を取り続けると、(
で停止し、そうでなければ、複数の特徴がある場合、偏導関数をとります。
と呼ばれるものに行き着きます。
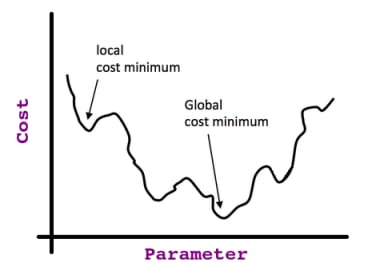
大域的最適化
に行き着く。
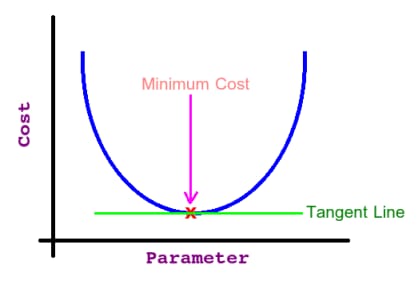
コストの最小点(つまり大域的最適点)で偏微分をとると、次のようになる。 スロープ 接線の 0 (となる(そうすれば目標に到達したことがわかる)。
がある場合のみ有効です。 凸型 がある場合のみ有効ですが、そうでない場合は、いわゆる 局所最適化 この非凸関数を考えてみよう。
これで、私たちがやっていることと用語のヘコミの関係を直感的に理解できたはずです。 派生的 , タンジェントライン , コスト関数 , 仮説 ...など。
余談:上記の直感は、Gradient Descent Algorithm(後述)にも関連します。
背景
線形近似。
関数が与えられると
f(x)
での正接を求めることができます。
x=a
. 接線の方程式は
L(x)
は
L(x)=f(a)+f′(a)(x−a)
.
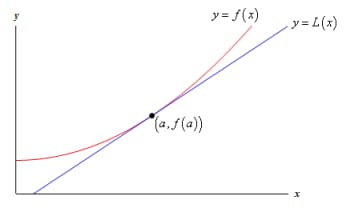
次の関数のグラフとその接線を見てみましょう。
このグラフから
x=a
の付近では、接線と関数は
ほぼ
のグラフになります。場合によっては、接線を使うこともある。
L(x)
を関数の近似値として使うこともある。
f(x)
の近くで
x=a
. このような場合、接線を " と呼びます。
線形近似
での関数への "。
x=a
.
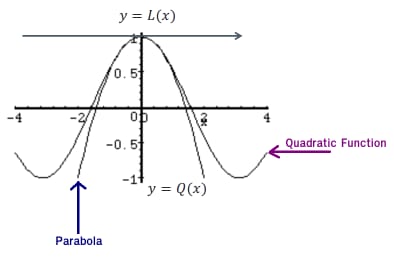
二次近似。
線形近似と同じですが、今回は曲線を扱うので はできません。 に近い点を見つけることができます。 0 のみを用いて 接線 .
代わりに 放物線 を使うことにする。
良い放物線を描くためには、放物線と二次関数の両方が、同じ
値
であること、同じ
一次導関数
であり、同じ
二次導関数
. この式は(
興味本位で
):
Qa(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)2/2
これで、詳細な比較を行う準備が整ったはずです。
メソッド間の比較
1. ニュートン法
での勾配降下ステップの動機付けを思い出してください。
x
で、2次関数(つまりコスト関数)を最小化します。
ニュートン法ではある意味で より良い 二次関数の最小化。 2次近似を使うのでより良い(つまり、最初の AND 第二 偏導関数)を使うからです。
これは、ヘシアンを使ったねじれた勾配降下法と想像できます (
の2階偏導関数からなる正方行列です。
n X n
).
さらに、ニュートン法の幾何学的解釈は、各反復において、近似的に
f(x)
の周りの二次関数で
xn
で、その二次関数の最大/最小に向かって一歩ずつ進む(高次元では、これは
鞍点
). なお、もし
f(x)
が2次関数である場合、厳密な極限は1つのステップで見つかります。
欠点。
-
それは、計算機的に 高い は、ヘシアン行列(つまり2次偏微分の計算)のためです。
-
に引き寄せられる。 サドルポイント これは多変数最適化で一般的な点です(つまり、この入力を最大点にするか最小点にするかで偏導関数が不一致になる点です!)。
2. Limited-memory Broyden-Fletcher-Goldfarb-Shanno Algorithm(限定メモリBroyden-Fletcher-Goldfarb-Shannoアルゴリズム)。
一言で言えば、ニュートン法のアナログであるが、ここではヘシアン行列は で近似されます。 は、勾配評価(または近似勾配評価)で指定された更新を使用します。言い換えれば、逆ヘッシアン行列への推定を使用します。
Limited-memoryという用語は、単に近似を暗黙的に表すいくつかのベクトルだけを保存することを意味します。
あえて言うなら、データセットが 小さい L-BFGSは他の手法と比較して相対的に最も性能が良く、特に多くのメモリを節約できるが、いくつかの" 深刻な 「
L-BFGS は他の手法と比較して、特に多くのメモリを節約することができます。
余談:このソルバーはバージョン 0.22 以降、LIBLINEAR に代わって sklearn LogisticRegression のデフォルトソルバーとなりました。
3. 大規模線形分類のためのライブラリ。
ロジスティック回帰や線形サポートベクターマシンをサポートする線形分類です。
ソルバーには、座標方向または座標超平面に沿って近似的な最小化を連続して行うことで最適化問題を解く、座標降下(CD)アルゴリズムが使用されています。
LIBLINEAR
はICML2008大規模学習チャレンジの優勝者である.この課題では
自動パラメータ選択
(別名 L1 正則化) を適用し、高次元のデータセット (
大規模な分類問題の解決に推奨される
)
欠点。
-
で引っかかることがあります。 非定常点 (すなわち、非最適点)に引っかかるかもしれません。
-
また、並列に実行することはできません。
-
真の多項式(マルチクラス)モデルを学習することはできません。その代わりに、最適化問題は「一対一」方式で分解されるため、すべてのクラスに対して別々の二値分類器が学習されます。
余談:Scikit Documentationによると。liblinear" ソルバーはバージョン0.22以前は歴史的な理由でデフォルトで使用されていたものです。それ以降は、Limited-memory Broyden-Fletcher-Goldfarb-Shanno Algorithmがデフォルトで使用されます。
4. ストキャスティック平均勾配。
SAG法は有限個の滑らかな凸関数の和を最適化する方法です。確率的勾配法(SG法)と同様、SAG法の反復コストは和の項数に依存しない。しかし 以前の勾配値を記憶しておくことで、SAG法はより速い収束速度を達成することができます。 ブラックボックスSG法よりも速い収束率を達成しています。
それは より速く に対して他のソルバよりも高速です。 大きい データセット(サンプル数と特徴数の両方が大きい場合)において、他のソルバーよりも優れた性能を発揮します。
欠点。
-
のみをサポートしています。
L2のみをサポートします。 -
そのメモリコストである
O(N)であるため、大規模なN( は,ほぼすべての勾配に対して,直近に計算された値を記憶しているので ).
5. SAGA:
SAGAソルバーは バリアント をサポートするSAGの変種であり、非平滑な ペナルティ L1 オプション(つまりL1正則化)もサポートしています。そのため、このソルバーは スパース 多項ロジスティック回帰に適しており、また 非常に大規模な データセットにも適しています。
余談:Scikit Documentationによると。SAGAソルバーが最適な場合が多いようです。
概要
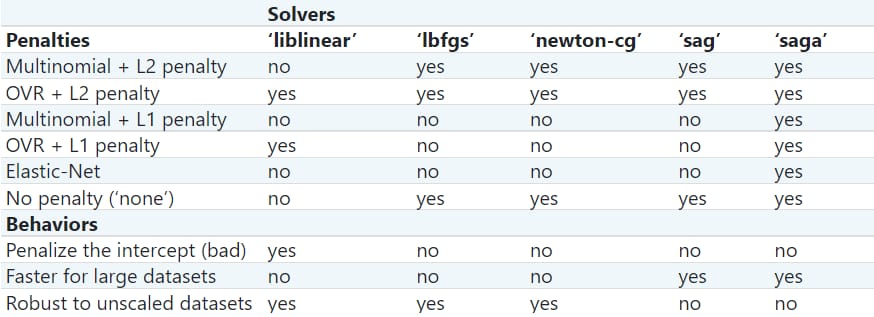
以下の表は Scikit ドキュメント
上記と同じリンクから表を更新しました(アクセス日:02/11/2021)。
関連
-
[解決済み] Pythonには文字列の'contains'サブストリングメソッドがありますか?
-
[解決済み] Pythonで現在時刻を取得する方法
-
[解決済み] Pythonで辞書に新しいキーを追加するにはどうすればよいですか?
-
[解決済み] Pythonで2つのリストを連結する方法は?
-
[解決済み] Pythonで例外を手動で発生(スロー)させる
-
[解決済み] Python 3で「1000000000000000 in range(1000000000000001)」はなぜ速いのですか?
-
[解決済み】Pythonに三項条件演算子はありますか?
-
[解決済み] SQLAlchemy: セッションの作成と再利用
-
[解決済み] バブルソートの宿題
-
[解決済み] Pandasの'Freq'タグにはどのような値が有効ですか?
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
[解決済み] PythonでのAWS Lambdaのインポートモジュールエラー
-
[解決済み] googletransがエラー 'NoneType' オブジェクトに 'group' 属性がない、と言って動かなくなった。
-
[解決済み] Pythonの要素別タプル演算(sumなど
-
[解決済み] Python 2.7サポート終了?
-
[解決済み] Pandasの'Freq'タグにはどのような値が有効ですか?
-
[解決済み] Pythonのargparseを使った隠し引数の作成
-
[解決済み] 文字列のリストを内容に基づいてフィルタリングする
-
[解決済み] Flask でグローバル変数はスレッドセーフか?リクエスト間でデータを共有するには?
-
[解決済み] djangoフレームワークでフォームフィールドから値を取得するには?
-
[解決済み] PySparkでデータフレームのカラムをString型からDouble型に変更する方法は?