[解決済み】Pythonで指数・対数カーブフィットを行うには？私は多項式フィットしか見つかりませんでした

質問

あるデータがあり、どの線が最もよく記述されているかを比較したい（異なる次数の多項式、指数または対数）。

PythonとNumpyを使っていますが、多項式フィットのための関数があります。 polyfit() . しかし、指数や対数のフィッティングにはそのような関数は見当たりません。

あるのでしょうか？または、それ以外の方法で解決する方法はありますか？

どのように解決するのですか？

装着方法 y = A + B ログ x であれば、ジャストフィット y に対して（ログ x ).

>>> x = numpy.array([1, 7, 20, 50, 79])
>>> y = numpy.array([10, 19, 30, 35, 51])
>>> numpy.polyfit(numpy.log(x), y, 1)
array([ 8.46295607,  6.61867463])
# y ≈ 8.46 log(x) + 6.62

フィッティング用 y = Ae ^Bx で、両辺の対数をとると、対数 y = log A + Bx . そこで、フィット（log y に対して x .

なお、フィッティング（log y の小さな値を強調することになります。 y が大きい場合、偏差が大きくなる。 y . これは polyfit (線形回帰)は∑を最小化することで機能します。 <サブ i (Δ Y ) ² = ∑ <サブ i ( Y <サブ i - Ŷ <サブ i ) ² . いつ Y <サブ i = ログ y <サブ i の場合、残基Δ Y <サブ i = Δ(log y <サブ i ) ≈ Δ y <サブ i / | y <サブ i |. ですから、たとえ polyfit が大きいため、非常に悪い判断をする。 y の場合、quot;divide-by-|になります。 y |" 要因がそれを補い、その結果 polyfit は小さい値を優先する。

これは、各エントリに、以下の値に比例した重みを与えることで緩和されます。 y . polyfit は重み付き最小二乗法をサポートしています。 w キーワード引数で指定します。

>>> x = numpy.array([10, 19, 30, 35, 51])
>>> y = numpy.array([1, 7, 20, 50, 79])
>>> numpy.polyfit(x, numpy.log(y), 1)
array([ 0.10502711, -0.40116352])
#    y ≈ exp(-0.401) * exp(0.105 * x) = 0.670 * exp(0.105 * x)
# (^ biased towards small values)
>>> numpy.polyfit(x, numpy.log(y), 1, w=numpy.sqrt(y))
array([ 0.06009446,  1.41648096])
#    y ≈ exp(1.42) * exp(0.0601 * x) = 4.12 * exp(0.0601 * x)
# (^ not so biased)

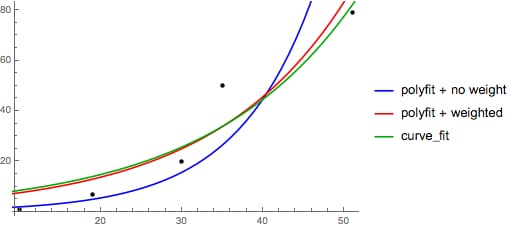
Excel、LibreOffice、およびほとんどの科学計算機では、指数回帰／傾向線に重みのない（偏った）公式が一般的に使用されていることに注意してください。 これらのプラットフォームと互換性のある結果を得たい場合は、たとえその方が良い結果が得られるとしても、重みを含めないでください。

さて、scipyが使えるのであれば scipy.optimize.curve_fit を使えば、変換なしでどんなモデルでもフィットさせることができます。

について y = A + B ログ x の場合、結果は変換方法と同じになります。

>>> x = numpy.array([1, 7, 20, 50, 79])
>>> y = numpy.array([10, 19, 30, 35, 51])
>>> scipy.optimize.curve_fit(lambda t,a,b: a+b*numpy.log(t),  x,  y)
(array([ 6.61867467,  8.46295606]), 
 array([[ 28.15948002,  -7.89609542],
        [ -7.89609542,   2.9857172 ]]))
# y ≈ 6.62 + 8.46 log(x)

について y = Ae ^Bx を計算するため、より適合度が高くなる。 y を直接表示します。しかし、初期化を行う必要があります。 curve_fit は目的のローカルミニマムに到達することができます。

>>> x = numpy.array([10, 19, 30, 35, 51])
>>> y = numpy.array([1, 7, 20, 50, 79])
>>> scipy.optimize.curve_fit(lambda t,a,b: a*numpy.exp(b*t),  x,  y)
(array([  5.60728326e-21,   9.99993501e-01]),
 array([[  4.14809412e-27,  -1.45078961e-08],
        [ -1.45078961e-08,   5.07411462e+10]]))
# oops, definitely wrong.
>>> scipy.optimize.curve_fit(lambda t,a,b: a*numpy.exp(b*t),  x,  y,  p0=(4, 0.1))
(array([ 4.88003249,  0.05531256]),
 array([[  1.01261314e+01,  -4.31940132e-02],
        [ -4.31940132e-02,   1.91188656e-04]]))
# y ≈ 4.88 exp(0.0553 x). much better.