データ構造 (python)
I. データ構造
student_list = [
{'name': 'zs', 'age': 12},
{'name': 'ls', 'age': 23}
]
student_dic = {
{'zs'}:{'sx',23},
{'ls'}:{'ls',24}
}
また、データを格納する構造をデータ構造といい、データを整理する方法をデータ構造といいます。
例えば、上記の生徒情報の格納方法ですが、リストとして整理されているのか、辞書を使って整理されているのか。
データ構造は、データの集合をどのように保存し、どのような形式をとるかを示すものである。
II. 線形テーブルの順列表
プログラムでは、(通常は同じ種類の)データ要素の集合を全体として管理し、その要素群を作成し、変数に記録し、関数を受け渡しするなどして利用する必要があることが多い。また、データ群に含まれる要素の数が変化する(要素が追加されたり削除されたりする)こともある。
このニーズに対する最も単純な解決策は、このような要素の集合をシーケンスとして考え、シーケンス内の要素の位置や順序を利用して、実際のアプリケーションで何らかの意味のある情報を表現したり、データ間の何らかの関係を表現したりすることである。
このような配列要素の集合の構成は、線形表として抽象化することができる。線形表は、ある種の要素の集まりであり、また要素間の順序関係を記録するものである。線形テーブルは最も基本的なデータ構造の1つで、実際のプログラムでも非常に広く使われており、より複雑なデータ構造を実装する際の基礎として用いられることも多い。
線形表には、実際の格納方法によって2つの実装モデルがあります。
(1). 連続した記憶領域に要素が順次格納され、要素間の順次関係がその格納順によって自然に表現される順次表。
(2). リンクによって構築された一連のブロックに要素が格納されているリンクテーブル。
リニアテーブルについて詳しく説明する前に、データがメモリ上に保持される形式をおさらいしておきましょう。
コンピュータのメモリは、実際にデータを保持し、CPUと直接やりとりするものなので、メモリが実際にどのようにモデル化されているかを見てみましょう。メモリの基本単位は1バイトで、1バイト=8ビットです。
例えば、a=1です。メモリ内に1を保持する空間を作るという話です。
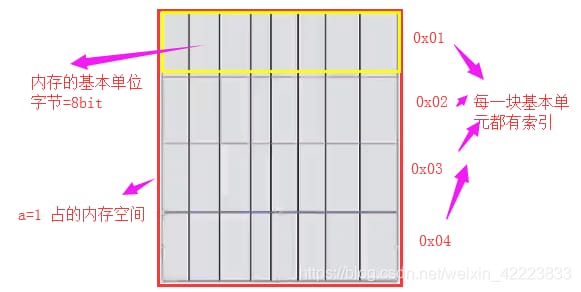
Pythonではすべてがオブジェクトであり、メモリにはデータ以外のものが存在するからです。28バイトは28*8=224ビットです。描画のために、我々は代わりに4バイトを使用することにします。
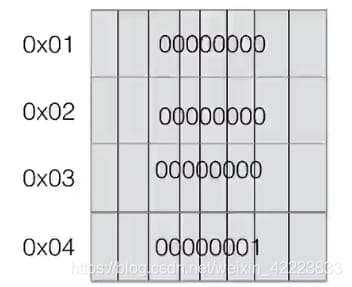
1. 配列表
要素を連続したストレージのブロックに順次格納し、要素間の順次関係は格納順によって自然に表現される。
例えば、Pythonのリストはシーケンシャルテーブルである。
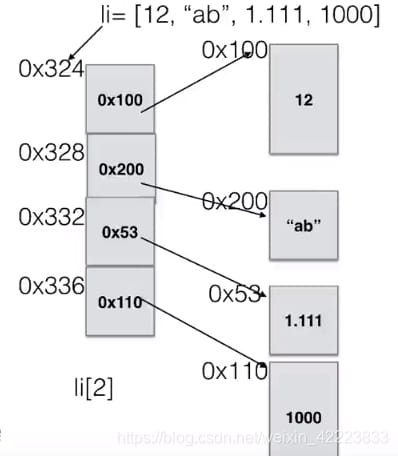
例えば、Li=[200,390,78,12112]のリストは、各要素が連続して格納されているメモリマップに相当します。そして、インデックスオフセットによって指定された要素を見つけることができます。

Li=[200,390,78,12112]のリストがどのようにメモリに格納され、どのように見つけるか見てみましょう。
Li変数は、実際にはメモリ空間の最初の要素のアドレスを実行するので、Li[3]の値を調べたい場合は、次のようになります。
CPUは実際にはLi[3]=0x23+3*4byteとなり、3つ下のポジションになります。

図aは連番テーブルの基本形を表しており、データ要素自体は連続して格納され、各要素は同じ固定サイズのメモリセルを占有し、要素の添え字はその論理アドレスで、要素が格納されている物理アドレス(実際のメモリアドレス)は、記憶領域の開始アドレスLoc(e0)に論理アドレス(i番目の要素)とメモリセルのサイズ(c)の積、すなわち、によって計算できる。
<スパン Loc(ei) = Loc(e0) + c*i です。
<スパン したがって、ある要素にアクセスする際に、最初から繰り返し計算する必要はなく、計算によって対応するアドレスを得ることができるのです。
要素のサイズが均一でない場合、実際のデータ要素は図bの外部要素のような形で別途格納する必要があり、オーダーテーブルの各セル位置に対応する要素(=リンク)のアドレス情報を格納することになる。各リンクは同じ量のストレージを必要とするので、上記の式で要素リンクの格納位置を計算し、リンクをたどって実際に格納されているデータ要素を見つけることができる。 図bのcは、もはやデータ要素のサイズではなく、通常非常に小さいリンクアドレスを格納するために必要なストレージの量であることに注意してください。
<スパン 図bのような連番表は、実際のデータに対するインデックスとも呼ばれ、最も単純なインデックス構造である。
Li=[12,'a',False] Int型は28バイト、bool型は28バイト、Falseは24バイトを占有します。文字列'a'は50バイトを占めます。したがって、それぞれのデータ型が異なる領域を開放し、メモリアドレスが連続しないので、上記の方法ではデータを保存できないので、要素の外側にある順次テーブルを使ってデータを保存することになります。各要素のメモリアドレスは同じメモリ空間を占有するため、各要素のメモリアドレスの保存が可能です
2. シーケンシャルテーブルの構成と実装
シーケンシャルテーブルはすでにPythonにカプセル化されているので、Python言語が実際にどのように実装しているかは検討しません。
実際に連番テーブルのようなデータ構造を実装した場合、どのように独自のデータ型を構築するかを検証してみましょう。


a.シーケンシャルテーブルの2つの実装

図aはオールインワン構造で、表情報を格納するセルが1つの格納領域に要素格納領域と連続して配置され、2つの部分のデータの全体が完全な順次表オブジェクトを形成しています。
<スパン モノリシックな構造は、全体的で管理しやすい。ただし、データ要素格納領域はテーブルオブジェクトの一部であるため、シーケンシャルテーブル作成後に要素格納領域が固定される。
<スパン 図bは、テーブルオブジェクトにはテーブル全体に関わる情報(容量や要素数など)のみを格納し、実際のデータ要素はリンクを介してベースのテーブルオブジェクトと関連付けられた別の要素格納領域に格納する分割構造である。

b.エレメントストアの交換
<スパン ワンピース構造とは、シーケンステーブル情報領域とデータ領域が連続して一緒に格納されているため、データ領域を置き換える場合は、全体、つまりシーケンステーブル・オブジェクト(シーケンステーブルの構造情報が格納されている領域を指す)全体が変更されたものを再配置すればよいからです。(例えば、Liに別の要素を追加したい場合、今追加した要素だけでなく、以前の情報もその中に保存するために新しい空間を開く必要がある)
<スパン デタッチャブル構造体のデータ領域を置き換える場合は、逐次表オブジェクトを変更せずに、表情報領域のデータ領域のリンクアドレスを更新するだけです。
そのため、分割構造を用いてシーケンシャルテーブルを実装することをお勧めします。
c.要素ストア展開
分割構造の逐次テーブルは、データ領域をより大きな記憶領域に置き換えれば、テーブルオブジェクトを変更することなく拡張でき、テーブルを使用しているすべての場所を変更する必要はない。プログラムの実行環境(コンピュータシステム)に空きストレージがある限り、このテーブル構造が一杯になって操作が不可能になることはない。
<スパン この手法で実装されたシーケンシャルテーブルは、使用に応じて容量が動的に変化することから、ダイナミックシーケンシャルテーブルと呼ばれている。
<スパン 拡大するための2つの戦略
- 1回の拡張につき10個のエレメントロケーションのように、拡張ごとに一定の数のストレージロケーションを追加する戦略は、線形成長と呼ぶことができます。
<スパン 特徴 省スペースでありながら、拡張操作や多くの操作を頻繁に行う。
- <スパン 1回の拡張で容量が2倍、例えばストレージ容量が2倍になります。
<スパン 特徴 実行する拡張操作の回数を減らすことができますが、スペースリソースを浪費する可能性があります。スペースと時間を交換する、お勧めの方法です。
<スパン 要約すると、最初の戦略は、いくつかの要素を追加することによってメモリ領域を拡大し、スペースを節約することです しかし、その拡張操作は頻繁に行われ、数も多い。
2番目の戦略であるダブルアップは、実行される拡張操作の回数を減らすことができますが、スペースリソースを浪費する可能性があります。スペースと時間を交換する、お勧めの方法です。
3. テーブルの連続操作
Pythonのリストはシーケンシャルテーブルです。リストにデータを追加する場合、append()メソッドやinsert(index,obj)メソッドを使って要素を追加していきます。では、実際にメモリ上でデータがどのように変化していくのかを調べてみましょう。
(1) 要素の追加
図のように、新しい要素111をオーダーテーブルに追加する方法は3つあります。
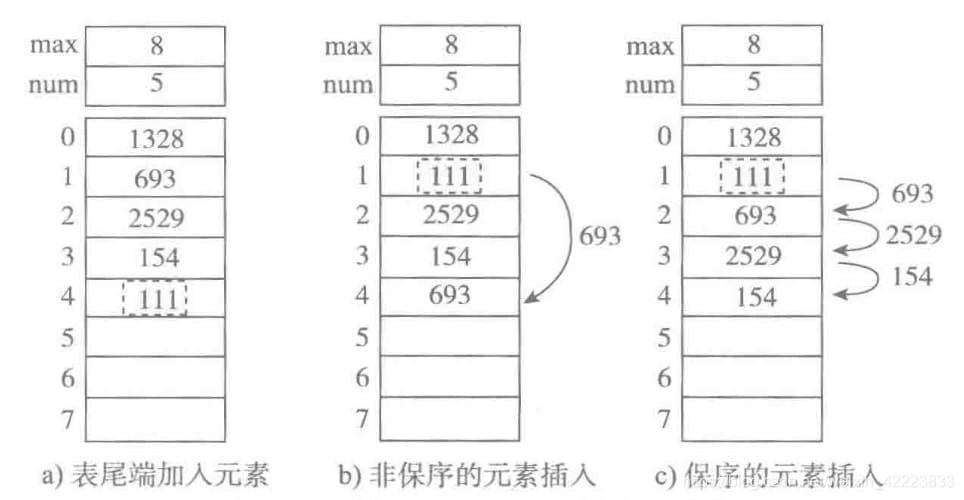
<スパン a. 末尾に要素を追加する .
b. 順序を保持しないjoin要素(珍しい) オリジナルの 693 要素が末尾に移動し 111 要素
指定された位置に挿入されます。この方法を使用した場合、要素の位置はめちゃくちゃになるため、保存されません。
c. 順序を保持する要素に となるような 693 要素、およびそれ以降の要素が1つずつ下に移動します。しかし、要素間の順序は変わらないので、順序保持と呼ばれる。
(2). 要素の削除
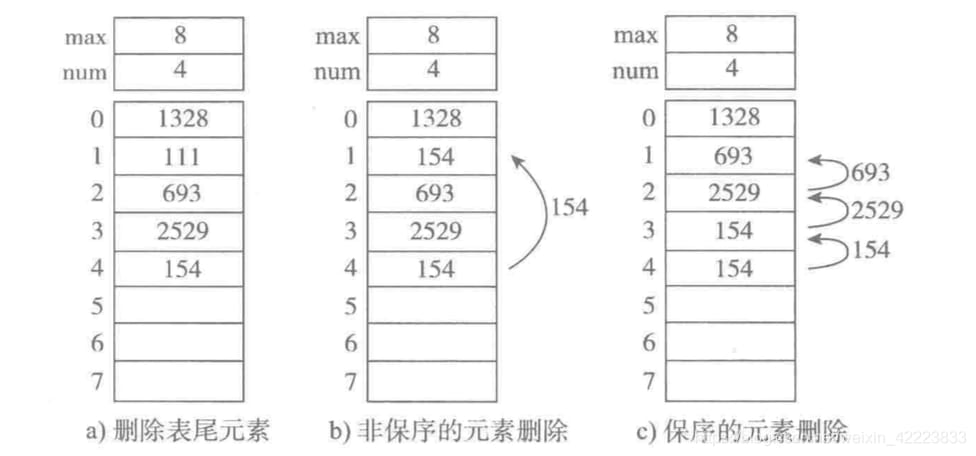
<スパン a. テーブルの末尾の要素を削除 末尾から直接要素を削除する。
b. 順序を守らない要素削除(一般的でない)である 例えば、最初の 154 に続いて 154 移動する
c. 順序を保持する要素が削除される、つまり 例えば、削除する 693 次の要素を順番に繰り上げる必要があります。
4. Pythonによる順次表
パイソン Pythonのリスト型とタプル型は、逐次表の実装技術を使用しており、先に説明した逐次表の特性をすべて備えています。
タプル はイミュータブル型、すなわち不変の連続した表であり、したがってその内部状態を変更する操作をサポートせず、その他の点ではリストと同様の性質を持っています。
(1)、リストの基本的な実装方法
Python 標準型リストは、追加・削除可能な要素数が可変の線形テーブルであり、様々な操作において既存の要素の順序を維持する(=順序保持)ほか、以下のような動作特性を持つ。
- <スパン 効率的な添え字(位置)ベースの要素アクセスと更新、この機能を満たすために、テーブルの要素が1つの連続した記憶領域に保持されるシーケンシャルテーブル技術を使用する必要があります。
- 任意に要素を追加することができ、要素を追加し続けてもテーブルオブジェクトのアイデンティティ(関数idで得られる値)は変わらない。 ( スプリットアプローチを使用する ) .
この機能を満たすためには、要素のストアを変更できることが必要であり、ストアを変更してもリストオブジェクトのIDが変わらないようにするためには、分割実装の手法しかない。
Pythonの公式実装では、listは分割技術を使って実装された動的な連番テーブルです。
Pythonの公式実装では、リストの実装は以下の戦略を採用しています。空のテーブル(または非常に小さなテーブル)を作成するとき、システムは8つの要素を保持できる記憶領域を割り当てます。挿入操作(insertまたはappend)を行うとき、要素の記憶領域がいっぱいになると、4倍大きな記憶領域に置き換わります。ただし、この時点ですでにテーブルが大きい場合(現在の閾値は5万、つまり5万要素)、戦略を変更し、2倍法を使用する。この方針変更は、空き記憶域が多くなりすぎるのを避けるために導入された。
III. 線形テーブルの連鎖テーブル
リンクテーブルが必要な理由
シーケンシャルテーブルは、構築時にデータサイズを事前に把握して連続したストレージを要求する必要があり、拡張時にはデータの再配置が必要なため、あまり柔軟な使い方ができません。
リンクテーブル構造では、コンピュータのメモリ空間をフルに活用し(連続したメモリを開放することなくデータを保持できる)、柔軟な動的メモリ管理を実現することができる。
1. リンクテーブルの定義
リンクリストは、一般的な基本データ構造である。線形表であるが、順次表のように連続的にデータを格納するのではなく、各ノード(データ格納単位)が次のノードの位置情報(アドレス)を保持する。

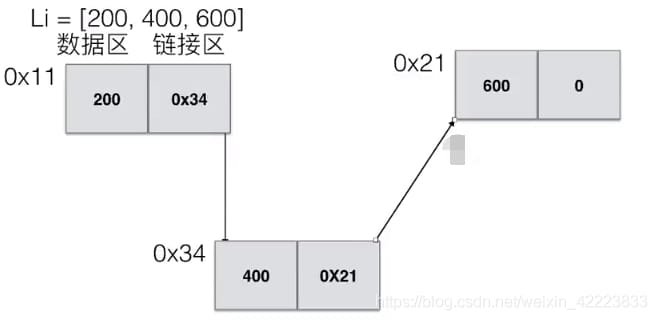
各ノードはデータだけでなく、次のノードのアドレスも保持している。このように、各要素はそのアドレスでリンクされています。これがリンクテーブルである。
一方向連鎖表と双方向連鎖表がある。
Lst=[2,3,4,5]です。
2. 一方向リンク表の構成と実装
単方向リンク表は、単リンク表とも呼ばれ、線が一方向しかないグラフを指し、リンク表の中で最も単純な形式である。その各ノードは、情報ドメイン(要素ドメイン)とリンクドメインの2つのドメインを含んでいる。このリンクは連鎖表の次のノードを指し、最後のノードのリンクフィールドはヌル値を指している。
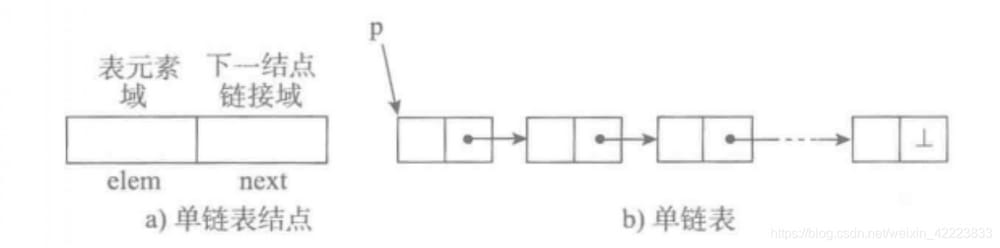
- table 要素 field elem は、特定のデータを保持するために使用される。
- リンクフィールドnextは、次のノードの位置(pythonでは識別子)を保持するために使用されます。
- 変数pはチェーンテーブルのヘッドノード(最初のノード)の位置を指し、そこからテーブル内のどのノードも見つけることができる。
(1) ノードの実装
class SingleNode(object):
"""node of a single linked table"""
def __init__(self, item):
# _item holds data elements
self.item = item
# _next is the identifier of the next node
self.next = None
(2) 単一のリンクテーブルの操作
is_empty() チェーンテーブルが空かどうか
length() チェーンテーブルの長さ
トラベル() チェーンテーブル全体をイテレートする
追加(アイテム) チェーンの先頭に要素を追加する
append(item) チェーンの末尾に要素を追加する
insert(pos, item) 指定された位置に要素を追加する
remove(アイテム) ノードを削除する
検索(アイテム) ノードが存在するかどうかを検索する
(3) 単一のリンクテーブルの実装
class SingleLinkList(object):
"""SingleLinkList"""
def __init__(self):
self._head = None
def is_empty(self):
"""Determine if the chain table is empty"""
return self._head is None
def length(self):
""""Chain length"""
# cur initially points to the head node
cur = self._head
count = 0
# tail node points to None, when the tail is not reached
while cur is not None:
count += 1
# Move cur back one node
cur = cur.next
return count
def travel(self):
"""traverse the chain"""
cur = self._head
while cur is not None:
print(cur.item, end=" ")
cur = cur.next
print()
<イグ
変数curはノードを表し、curが300以降のノードに移動しても、それ以上はないのでNoneとなる。したがって、ループのボディ条件にはcur!=Noneを使用する。
鎖の長さを計算するには、各ノードのリンク領域を参照し、アドレスがあれば次のノードがあることを意味し、最後のノードのリンク領域はNoneなので、Noneかどうかを判断することで終点にいるかどうかを判断することが可能です。
<スパン ヘッダーに要素を追加する
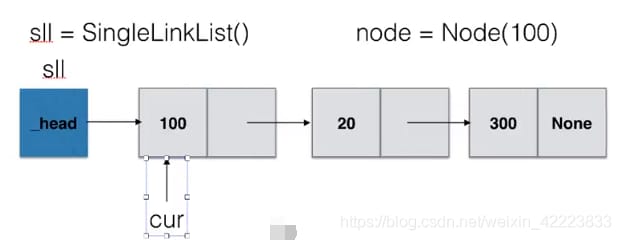
def add(self, item):
"""Add element to header"""
# Create one first to hold the value of the item node
node = SingleNode(item)
# Point the new node's link field next to the head node, i.e. the location pointed to by _head
node.next = self._head
# Point the head of the chain table _head to the new node
self._head = node
末尾に要素を追加する
def append(self, item):
"""append element at the end"""
node = SingleNode(item)
# first determine if the chain is empty, if it is, then point _head to the new node
if self.is_empty():
self._head = node
# If not empty, find the tail and point the tail node's next to the new node
else:
cur = self._head
while cur.next is not None:
cur = cur.next
cur.next = node
<スパン 指定した位置に要素を追加する

def insert(self, index, item):
"""Add element at specified position"""
# If the specified position pos is before the first element, then perform a head insertion
if index <= 0:
self.add(item)
# If the specified position is beyond the end of the chain, then perform the tail insertion
elif index > (self.length() - 1):
self.append(item)
# Find the specified position
else:
node = SingleNode(item)
count = 0
# pre is used to point to the specified position pos the previous position pos-1, the initial move from the head node to the specified position
pre = self._head
while count < (index - 1):
count += 1
pre = pre.next
# first point the new node node's next to the node at the insertion position
node.next = pre.next
# point the next node at the insertion position to the new node
pre.next = node
<スパン ノードの削除

def remove(self, item):
"""Remove node"""
cur = self._head
pre = None
while cur is not None:
# The specified element is found
if cur.item == item:
# If the first one is the deleted node
if not pre:
# Point the head pointer to the node after the head node
self._head = cur.next
else:
# Point the next node before the deleted position to the next node after the deleted position
pre.next = cur.next
break
else:
# Continue to move nodes back in the chain
pre = cur
cur = cur.next
ノードが存在するかどうかを調べる
def search(self, item):
"""Chain table to find if node exists and return True or False""""
cur = self._head
while cur is not None:
if cur.item == item:
return True
cur = cur.next
return False
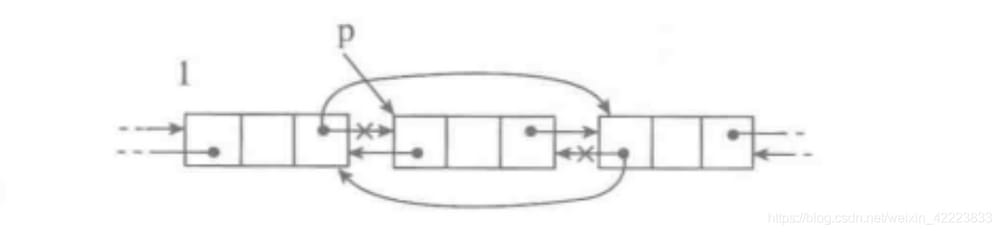
3. 双方向リンクテーブル
より複雑なリンクテーブルとして、quot;双方向リンクテーブル、またはquot;両面リンクテーブルがあります。各ノードは2つのリンクを持ちます。1つは前のノードへのリンクで、最初のノードである場合はnullを指し、もう1つは次のノードへのリンクで、最後のノードである場合はnullを指し示します。

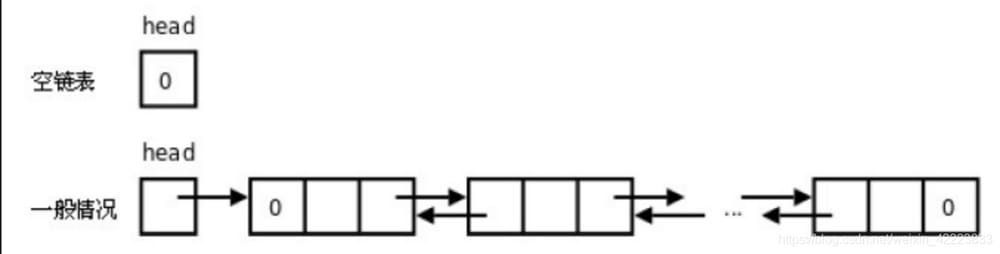
(1) 双方向リンクテーブルの動作について
is_empty() チェーンテーブルが空かどうか
length() チェーンテーブルの長さ
トラベル() リンクされたテーブルを反復処理する
追加(アイテム) チェーンテーブルの先頭を追加する
append(item) チェーンの末尾に追加する
insert(pos, item) 追加する位置を指定する
remove(アイテム) ノードを削除する
検索(アイテム) ノードが存在するかどうかを検索する
(2) 双方向リンクテーブルの実装
class Node(object):
"""Bidirectional linked table node"""
def __init__(self, item):
self.item = item
self.next = None
self.prev = None
class DLinkList(object):
"""Two-way linked list"""
def __init__(self):
self._head = None
def is_empty(self):
"""Determine if the chain table is empty"""
return self._head == None
def length(self):
"""Return the length of the chain table"""
cur = self._head
count = 0
while cur is not None:
count += 1
cur = cur.next
return count
def travel(self):
"""traverse the chain"""
cur = self._head
while cur is not None:
print(cur.item, end=" ")
cur = cur.next
print("")
def add(self, item):
"""head insert element"""
node = Node(item)
if self.is_empty():
# If it's an empty chain table, point _head to node
self._head = node
else:
# Point node's next to _head's head node
node.next = self._head
# point the prev of the head node of _head to node
self._head.prev = node
# point _head to node
self._head = node
def append(self, item):
"""tail insert element"""
node = Node(item)
if self.is_empty():
# If it's an empty chain table, point _head to node
self._head = node
else:
# Move to the end of the chain
cur = self._head
while cur.next is not None:
cur = cur.next
# Point the tail node cur's next to node
cur.next = node
# point the prev of node to cur
node.prev = cur
def search(self, item):
"""Find if element exists"""
cur = self._head
while cur is not None:
if cur.item == item:
return True
cur = cur.next
return False
Add() は操作を追加します。

append()操作。

Insert()操作
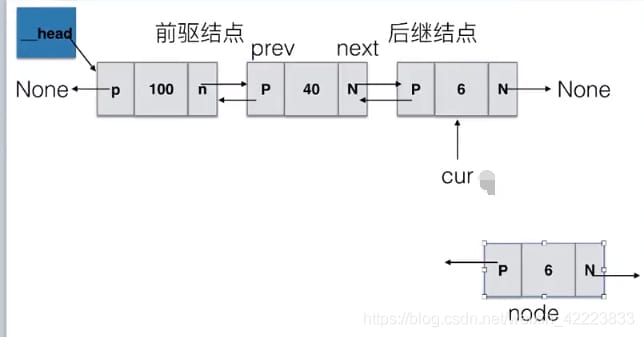
注:cur.prevはプリカーサ・ノード・オブジェクトを指します。
remove() による削除操作
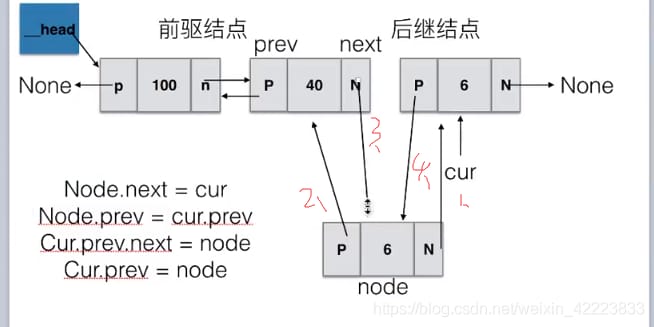
<スパン 指定した位置にノードを挿入する
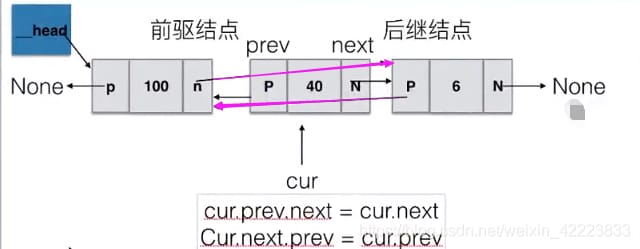
def insert(self, pos, item):
"""Add node at specified position"""
if pos <= 0:
self.add(item)
elif pos > (self.length() - 1):
self.append(item)
else:
node = Node(item)
cur = self._head
count = 0
# Move to the position before the specified position
while count < (pos - 1):
count += 1
cur = cur.next
# Point node's prev to cur
node.prev = cur
# point node's next node to cur
node.next = cur.next
# point the next node of cur's prev to node
cur.next.prev = node
# point cur's next to node
cur.next = node
<スパン 要素の削除
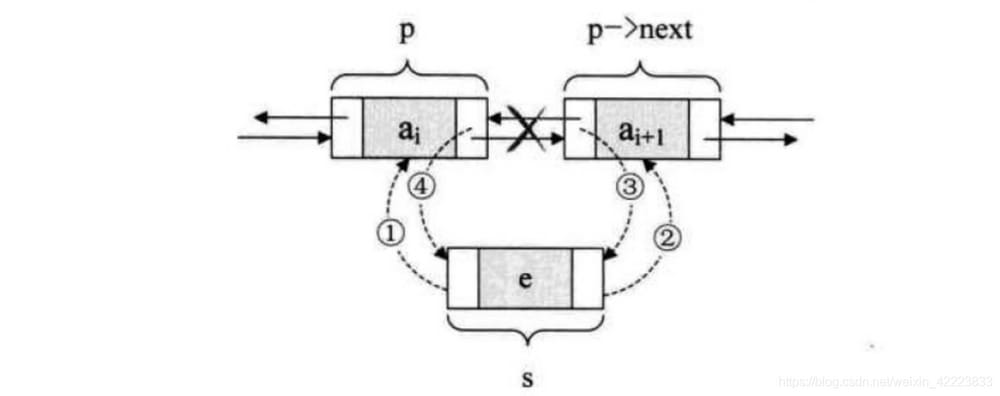
def remove(self, item):
"""Remove element"""
if self.is_empty():
return
else:
cur = self._head
if cur.item == item:
# If the element of the first node is the element to be deleted
if cur.next == None:
# If this is the only node in the chain
self._head = None
else:
# Set the prev of the second node to None
cur.next.prev = None
# Point _head to the second node
self._head = cur.next
return
while cur ! = None:
if cur.item == item:
# point the next node of cur to the previous node of cur
cur.prev.next = cur.next
# point the prev of the node after cur to the node before cur
cur.next.prev = cur.prev
break
cur = cur.next
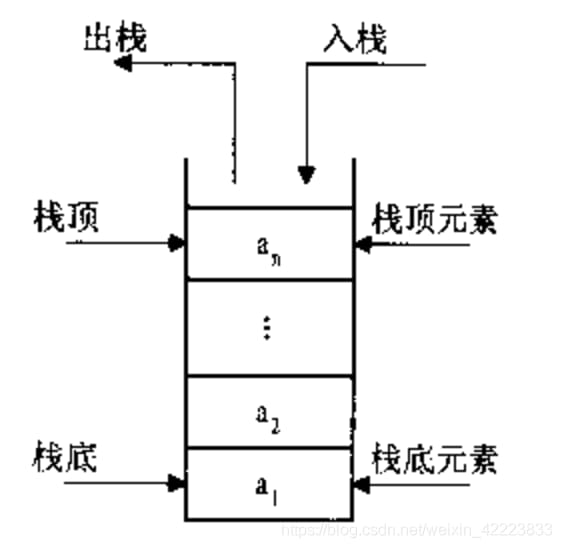
IV. スタック
スタック(stack)は、場所によってはスタックと呼ばれ、データ要素の預け入れ、アクセス、削除が可能な容器である。容器の一端(トップインジケータ、英語ではtopと呼ばれる)だけに、データを追加する操作(英語ではpush)とデータを出力する操作(英語ではpop)を許可する点が特徴的である。位置の概念がないため、いつでもアクセス・削除できる要素は、前回最後に預けた要素であることが保証され、デフォルトのアクセス順が定義される。
スタックデータ構造は片方の端しか操作できないので、LIFO(Last In First Out)の原則で動作する。
スタックとキューは操作レベルを、シーケンシャルテーブルとチェーンはデータの格納方法を研究していることに注意してください。
シーケンシャルテーブルとチェーンをスタックとキューに見えるように修正します。
(1) スタックの動作
- スタック() 空のスタックを新規に作成する
- push(アイテム) 新しい要素itemをスタックの一番上に追加する
- pop() スタックの先頭の要素をポップします
- peek() スタックの先頭の要素を返します。
- is_empty() スタックが空かどうかを判断する
- size() スタック内の要素数を返す
(2) スタック構造の実装
スタックは、シーケンシャルテーブルまたはリンクテーブルとして実装することができます。
class Stack(object):
"""stack"""
def __init__(self):
self.items = []
def is_empty(self):
"""Determine if it is empty"""
return self.items == []
def push(self, item):
"""add element"""
self.items.append(item)
def pop(self):
"""pop element"""
return self.items.pop()
def peek(self):
"""Return the top element of the stack"""
return self.items[len(self.items) - 1]
def size(self):
"""Return the size of the stack"""
return len(self.items)
if __name__ == "__main__":
stack = Stack()
stack.push("hello")
stack.push("world")
stack.push("itcast")
print(stack.size())
print(stack.peek())
print(stack.pop())
print(stack.pop())
print(stack.pop())
print(stack.size())
V. キュー
キューは、一端が挿入操作、他端が削除操作のみを許可する線形テーブルです。
<スパン キューは、FIFO(First In First Out)線形テーブルで、末端で挿入を、先頭で削除を許可します。待ち行列は、中間部での操作を許しません! 待ち行列をq = (a1, a2, ......, an)とすると、a1が先頭要素、anが末尾要素になります。こうすれば、削除するときは常にa1から始め、挿入するときは常に待ち行列の最後尾にすることができる。これはまた、列の先頭が最初に出てきて、最後に来た人はもちろん列の最後にいるという、私たちの普段の生活習慣にもより合致している。
(1) 待ち行列の運用について
- キュー() 空のキューを作成します
- enqueue(アイテム) キューにアイテム要素を追加する
- dequeue() キューの先頭から要素を削除します。
- is_empty() キューが空かどうかを判定する
- size() キューのサイズを返します。
(2) キューの実装
キューはシーケンシャルテーブルで実装することができます。
class Queue(object):
"""Queue"""
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def enqueue(self, item):
"""into the queue"""
self.items.insert(0, item)
def dequeue(self):
"""out of queue"""
return self.items.pop()
def size(self):
"""return size"""
return len(self.items)
if __name__ == "__main__":
q = Queue()
q.enqueue("hello")
q.enqueue("world")
q.enqueue("itcast")
print(q.size())
print(q.dequeue())
print(q.dequeue())
print(q.dequeue())
(3) ダブルエンド・キュー
ダブルエンド型キュー(deque、正式名称:double-ended queue)は、キューとスタックの性質を併せ持つデータ構造である。
ダブルエンド型待ち行列の要素は両端からポップすることができ、その限定された挿入と削除の操作はテーブルの両端で実行されます。ダブルエンド型キューは、キューの両端からキューイン・アウトすることができます。

1. ダブルエンドキューの動作
- Deque() 空のダブルエンド・キューを作成します
- add_front(アイテム) キューの先頭からアイテム要素を追加する
- add_rear(item) キューの末尾からitem要素を追加する
- remove_front() キューの先頭から項目要素を削除する
- remove_rear() キューの末尾からアイテム要素を削除する
- is_empty() ダブルエンドのキューが空かどうか判断する
- size() キューのサイズを返します。
2. ダブルエンドキューの実装
class Deque(object):
"""Double-ended queue"""
def __init__(self):
self.items = []
def is_empty(self):
"""Determine if the queue is empty"""
return self.items == []
def add_front(self, item):
"""Add an element to the head of the queue"""
self.items.insert(0, item)
def add_rear(self, item):
"""Add an element to the end of the queue"""
self.items.append(item)
def remove_front(self):
"""Remove elements from the head of the queue"""
return self.items.pop(0)
def remove_rear(self):
"""Remove elements from the end of the queue"""
return self.items.pop()
def size(self):
"""return queue size"""
return len(self.items)
if __name__ == "__main__":
deque = Deque()
deque.add_front(1)
deque.add_front(2)
deque.add_rear(3)
deque.add_rear(4)
print(deque.size())
print(deque.remove_front())
print(deque.remove_front())
print(deque.remove_rear())
print(deque.remove_rear())
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
ハートビート・エフェクトのためのHTML+CSS
-
HTML ホテル フォームによるフィルタリング
-
HTML+cssのボックスモデル例(円、半円など)「border-radius」使いやすい
-
HTMLテーブルのテーブル分割とマージ(colspan, rowspan)
-
ランダム・ネームドロッパーを実装するためのhtmlサンプルコード
-
Html階層型ボックスシャドウ効果サンプルコード
-
QQの一時的なダイアログボックスをポップアップし、友人を追加せずにオンラインで話す効果を達成する方法
-
sublime / vscodeショートカットHTMLコード生成の実装
-
HTMLページを縮小した後にスクロールバーを表示するサンプルコード
-
html のリストボックス、テキストフィールド、ファイルフィールドのコード例