[解決済み] Pythonによる一律コスト探索

質問

Pythonで簡単なグラフのデータ構造を実装したのですが、以下のような構造になっています。このコードは関数や変数の意味を明らかにするためのものですが、かなり自明なものなので読み飛ばしていただいて結構です。

# Node data structure
class Node: 

    def __init__(self, label):        
        self.out_edges = []
        self.label = label
        self.is_goal = False


    def add_edge(self, node, weight = 0):          
        self.out_edges.append(Edge(node, weight))


# Edge data structure
class Edge:

    def __init__(self, node, weight = 0):          
        self.node = node
        self.weight = weight

    def to(self):                                  
        return self.node


# Graph data structure, utilises classes Node and Edge
class Graph:    

    def __init__(self):                             
        self.nodes = []

    # some other functions here populate the graph, and randomly select three goal nodes.

今、私は ユニフォームコスト検索 (すなわち，最短経路を保証する優先度付きBFS)であり，与えられたノードから開始される v そして、3つのゴールノードのうちの1つへの最短経路を(リスト形式で)返す。によって ゴールノード という属性を持つノードを意味します。 is_goal をtrueに設定します。

これは私の実装です。

def ucs(G, v):
    visited = set()                  # set of visited nodes
    visited.add(v)                   # mark the starting vertex as visited
    q = queue.PriorityQueue()        # we store vertices in the (priority) queue as tuples with cumulative cost
    q.put((0, v))                    # add the starting node, this has zero *cumulative* cost   
    goal_node = None                 # this will be set as the goal node if one is found
    parents = {v:None}               # this dictionary contains the parent of each node, necessary for path construction

    while not q.empty():             # while the queue is nonempty
        dequeued_item = q.get()        
        current_node = dequeued_item[1]             # get node at top of queue
        current_node_priority = dequeued_item[0]    # get the cumulative priority for later

        if current_node.is_goal:                    # if the current node is the goal
            path_to_goal = [current_node]           # the path to the goal ends with the current node (obviously)
            prev_node = current_node                # set the previous node to be the current node (this will changed with each iteration)

            while prev_node != v:                   # go back up the path using parents, and add to path
                parent = parents[prev_node]
                path_to_goal.append(parent)   
                prev_node = parent

            path_to_goal.reverse()                  # reverse the path
            return path_to_goal                     # return it

        else:
            for edge in current_node.out_edges:     # otherwise, for each adjacent node
                child = edge.to()                   # (avoid calling .to() in future)

                if child not in visited:            # if it is not visited
                    visited.add(child)              # mark it as visited
                    parents[child] = current_node   # set the current node as the parent of child
                    q.put((current_node_priority + edge.weight, child)) # and enqueue it with *cumulative* priority

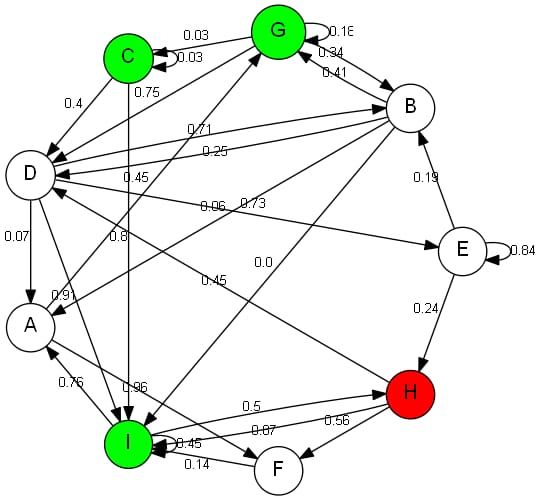
さて、多くのテストと他のアルゴリズムとの比較の結果、この実装はかなりうまくいっているようです - このグラフで試してみるまでは。

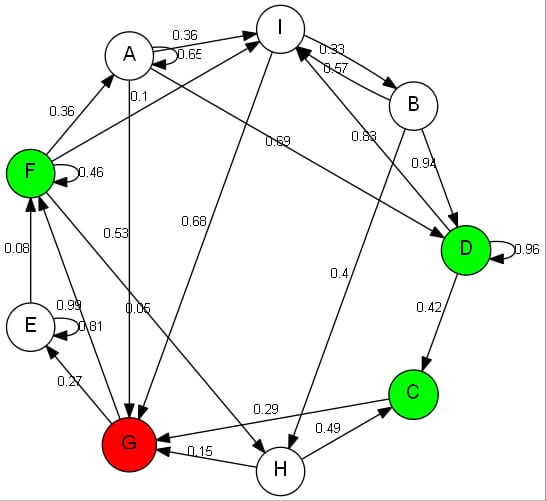
どんな理由であれ ucs(G,v) はパスを返しました。 H -> I であり、コストが 0.87 であるのに対し、パス H -> F -> I 0.71であった（このパスはDFSを実行することで得られた）。次のグラフも誤った経路を与えています。

このアルゴリズムでは G -> F ではなく G -> E -> F また、DFSで得られた これらの稀なケースで観察できる唯一のパターンは、選択されたゴールノードが常にループを持つという事実です。しかし、何が問題なのかがわからない。何かヒントがあれば、ぜひ教えてください。

解決方法は？

通常、検索では、ノードへのパスをキューの一部として保持することが多いですね。これはあまりメモリ効率はよくありませんが、実装は安く済みます。

親マップが必要な場合は、子マップがキューの先頭にあるときだけ親マップを更新するのが安全であることを覚えておいてください。そのときだけ、アルゴリズムは現在のノードへの最短経路を決定しているのです。

def ucs(G, v):
    visited = set()                  # set of visited nodes
    q = queue.PriorityQueue()        # we store vertices in the (priority) queue as tuples 
                                     # (f, n, path), with
                                     # f: the cumulative cost,
                                     # n: the current node,
                                     # path: the path that led to the expansion of the current node
    q.put((0, v, [v]))               # add the starting node, this has zero *cumulative* cost 
                                     # and it's path contains only itself.

    while not q.empty():             # while the queue is nonempty
        f, current_node, path = q.get()
        visited.add(current_node)    # mark node visited on expansion,
                                     # only now we know we are on the cheapest path to
                                     # the current node.

        if current_node.is_goal:     # if the current node is a goal
            return path              # return its path
        else:
            for edge in in current_node.out_edges:
                child = edge.to()
                if child not in visited:
                    q.put((current_node_priority + edge.weight, child, path + [child]))

注：実際にテストしたわけではないので、すぐに動かない場合は遠慮なくコメントしてください。