[解決済み] O(N log N)の複雑さ - 線形に似ている？

質問

そこで、こんなつまらない質問をすると埋もれてしまうと思うのですが、ちょっとわからないことがあります。

私はJavaとCでクイックソートを実装し、いくつかの基本的な比較をしていました。グラフは2本の直線で、10万個のランダムな整数を処理した場合、Cの方がJavaのものより4ms速くなりました。

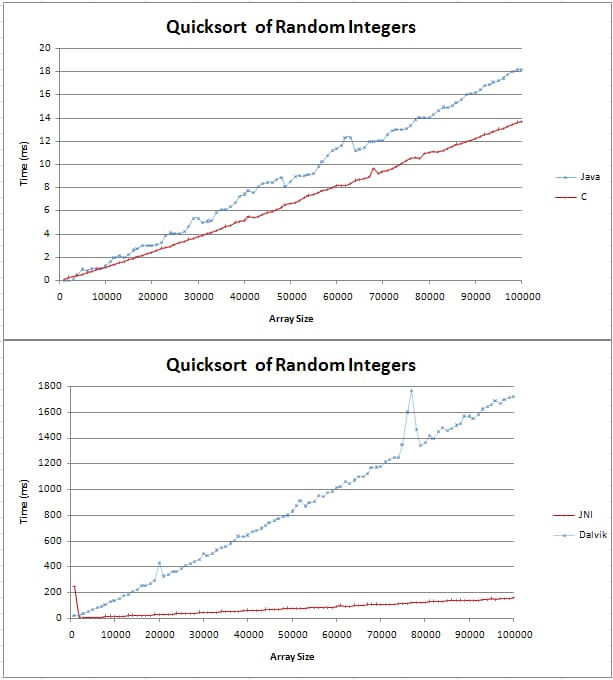
私のテストのコードは、ここにあります。

アンドロイドベンチマーク

(n log n)の線がどのようなものかわからなかったのですが、まさかまっすぐとは思いませんでした。私はただ、これが期待される結果であり、私のコードでエラーを見つけようとすべきではないことを確認したかったのです。

数式をエクセルに突っ込んでみたところ、基数10の場合、最初にキンクがある直線になるようです。これは、log(n)とlog(n+1)の差が直線的に増加するからでしょうか？

ありがとうございます。

ガヴ

解決方法は？

グラフを大きくしてみると、O(n logn)が直線でないことがわかると思います。しかし、そうです、かなり直線に近い挙動をしているのです。その理由を知るには、いくつかの非常に大きな数の対数を取ればよいのです。

例えば（10進法）。

log(1000000) = 6
log(1000000000) = 9
…

つまり、1,000,000個の数字をソートするために、O(n logn)ソートはわずか6倍を追加するだけです（ほとんどのソートアルゴリズムは2の底対数に依存するので、もう少しだけ増えるかもしれません）。大したことではありません。

実は、この対数係数は だから ほとんどの桁の大きさでは、確立されたO(n logn)アルゴリズムが線形時間アルゴリズムに勝るほど、非常に小さいものです。その代表的な例が、接尾辞配列のデータ構造の作成です。

最近、簡単なケースで食傷気味 短い文字列のクイックソートを基数ソートで改善しようとしたとき . しかし、比較的短い文字列の場合は、基数ソートの方がクイックソートよりも高速であることがわかりました。