[解決済み] numpy.fft.fft と numpy.fft.fftfreq の違いは何ですか？

質問

時系列データを分析しており、5つの主要な周波数成分を抽出し、機械学習モデルの学習用特徴量として使用したいと考えています。私のデータセットは 921 x 10080 . 各行が時系列で、全部で921個あります。

これを実現するための方法を探っているうちに、以下のような様々な関数に出会いました。 numpy.fft.fft , numpy.fft.fftfreq と DFT ... 質問ですが、これらの関数はデータセットに対して何をするのでしょうか、また、これらの関数の違いは何でしょうか？

について Numpy.fft.fft と、Numpyのドキュメントに書かれています。

Compute the one-dimensional discrete Fourier Transform.

This function computes the one-dimensional n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm [CT].

一方 numpy.fft.fftfreq :

numpy.fft.fftfreq(n, d=1.0)
Return the Discrete Fourier Transform sample frequencies.

The returned float array f contains the frequency bin centers in cycles per unit of the sample spacing (with zero at the start). For instance, if the sample spacing is in seconds, then the frequency unit is cycles/second.

しかし、信号処理に関する背景知識がないためか、これでは話になりません。私の場合、例えばデータセットの各行について最初の5つの主要な周波数と振幅の成分を抽出する場合、どの関数を使用すればよいのでしょうか？ありがとうございます。

更新しました。

使用方法 fft は以下のような結果を返しました。各時系列の最初の5つの周波数と振幅の値を取得するつもりでしたが、周波数成分なのでしょうか？

以下はそのコードです。

def get_fft_values(y_values, T, N, f_s):
    f_values = np.linspace(0.0, 1.0/(2.0*T), N//2)
    fft_values_ = rfft(y_values)
    fft_values = 2.0/N * np.abs(fft_values_[0:N//2])
    return f_values[0:5], fft_values[0:5]  #f_values - frequency(length = 5040) ; fft_values - amplitude (length = 5040)

t_n = 1
N = 10080
T = t_n / N
f_s = 1/T

result = pd.DataFrame(df.apply(lambda x: get_fft_values(x, T, N, f_s), axis =1)) 
result

と出力します。

0   ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [52.91299603174603, 1.2744877093061115, 2.47064631896607, 1.4657299825335832, 1.9362280837538701])
1   ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [57.50430555555556, 4.126212552498241, 2.045294347349226, 0.7878668631936439, 2.6093502232989976])
2   ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [52.05765873015873, 0.7214089616631307, 1.8547819994826562, 1.3859749465142301, 1.1848485830307878])
3   ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [53.68928571428572, 0.44281647644149114, 0.3880646059685434, 2.3932194091895043, 0.22048418335196407])
4   ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [52.049007936507934, 0.08026717757664162, 1.122163085234073, 1.2300320578011028, 0.01109727616896663])
... ...
916 ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [74.39303571428572, 2.7956204803382096, 1.788360577194303, 0.8660509272194551, 0.530400826933975])
917 ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [51.88751984126984, 1.5768804453161231, 0.9932384706239461, 0.7803585797514547, 1.6151532436755451])
918 ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [52.16263888888889, 1.8672674706267687, 0.9955183554654834, 1.0993971449470716, 1.6476405255363171])
919 ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [59.22579365079365, 2.1082518972190183, 3.686245044113031, 1.6247500816133893, 1.9790245755039324])
920 ([0.0, 1.000198452073824, 2.000396904147648, 3.0005953562214724, 4.000793808295296], [59.32333333333333, 4.374568790482763, 1.3313693716184536, 0.21391538068483704, 1.414774377287436])

解決方法は？

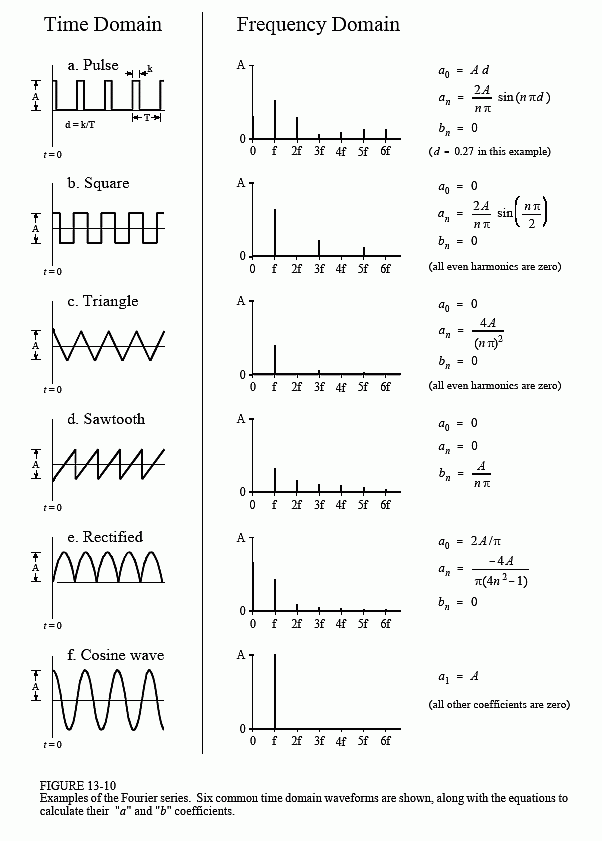
まず、信号には時間領域と周波数領域の表現があることを理解する必要があります。下の図は、いくつかの一般的な基本信号の種類と、それらの時間領域と周波数領域の表現を示しています。

fftとftfreqの違いを説明するために使用するサインカーブに注目してください。

フーリエ変換は、時間領域と周波数領域の表現の間のポータルです。したがって

numpy.fft.fft() - はフーリエ変換を返します。これは実部と虚部の両方を持ちます。実数部と虚数部は、データウィンドウの中心を中心とした対称性（偶数と奇数）に興味がない限り、それ自体では特に役に立ちません。

numpy.fft.fftfreq - は、周波数ビンの中心をサンプル間隔の単位あたりのサイクルで表した float 配列を返します。

は numpy.fft.fft() メソッドは、ftを適切に分離できるような周波数を得るための方法です。

これは例で説明するのが一番わかりやすいと思います。

import numpy as np
import matplotlib.pyplot as plt

#fs is sampling frequency
fs = 100.0
time = np.linspace(0,10,int(10*fs),endpoint=False)

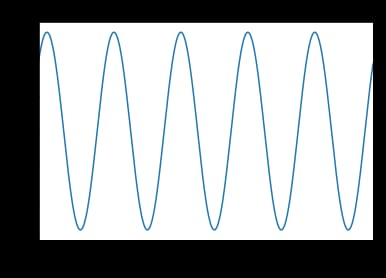
#wave is the sum of sine wave(1Hz) and cosine wave(10 Hz)
wave = np.sin(np.pi*time)+ np.cos(np.pi*time)
#wave = np.exp(2j * np.pi * time )

plt.plot(time, wave)
plt.xlim(0,10)
plt.xlabel("time (second)")
plt.title('Original Signal in Time Domain')

plt.show()

# Compute the one-dimensional discrete Fourier Transform.

fft_wave = np.fft.fft(wave)

# Compute the Discrete Fourier Transform sample frequencies.

fft_fre = np.fft.fftfreq(n=wave.size, d=1/fs)

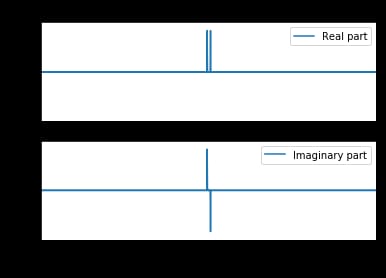
plt.subplot(211)
plt.plot(fft_fre, fft_wave.real, label="Real part")
plt.xlim(-50,50)
plt.ylim(-600,600)
plt.legend(loc=1)
plt.title("FFT in Frequency Domain")

plt.subplot(212)
plt.plot(fft_fre, fft_wave.imag,label="Imaginary part")
plt.legend(loc=1)
plt.xlim(-50,50)
plt.ylim(-600,600)
plt.xlabel("frequency (Hz)")

plt.show()