NumPy学習ノート(2) - 配列と基本的な行列演算

numpyはまだ非常に強力なので、ここではあなたの便宜のために、そして私が自分でコーディングするときに見つけるために、いくつかの基本的な行列演算を紹介します。

まず、動画を見ながら、プログラムを書くときに何を実現する必要があるのかを確認することです。調べるだけで十分ですし、使っていくうちに自然と覚えていくものです。

C++入門Plusの本をパラパラめくって、使わないで言語を覚えるのは裏を読んで表を忘れるという悲しいことだったのを覚えています。

1. 関数ライブラリのインポート

import numpy #or
import numpy as np

2. 基本操作

**2.1.**和算 .sum()
**2.2.**Sum the maximum .max()
**2.3.**Minimum .min()
**2.4.**Seek the mean .mean()

import numpy as np
test1 = np.array([[5, 10, 15],
	        [20, 25, 30],
	        [35, 40, 45]])
test1.sum()
# Output 225
test1.max()
# Output 45
test1.min()
# Output 5
test1.mean()
# Output 25.0

**2.5.**行列の行の総和 .sum(axis=1)

test1 = np.array([[5, 10, 15],
	        [20, 25, 30],
	        [35, 40, 45]])
test1.sum(axis=1)
# Output array([30, 75, 120])

**2.6.** 行列の総和 .sum(axis=0)

test1 = np.array([[5, 10, 15],
	        [20, 25, 30],
	        [35, 40, 45]])
test1.sum(axis=0)
# Output array([60, 75, 90])

**2.7.** 行列の乗算

import numpy as np
a = np.array([[1, 2],
              [3, 4]])
b = np.array([[5, 6],
              [7, 8]])
print (a*b) # Multiply the elements in the corresponding positions
print (a.dot(b)) # Matrix multiplication
print (np.dot(a, b)) # Matrix multiplication, as above
# Output [[5 12]
       [21 32]]
      [[19 22]]
       [43 50]]
      [[19 22]]
       [43 50]]  

**2.8. 四角い要素：a 2

a = np.range(4)
print (a)
print (a**2)
# Output [0, 1, 2, 3]
      [0, 1, 4, 9]

**2.9.** 要素のeのn乗: np.exp(test)
要素の開ルート：np.sqrt(test)

import numpy as np
test = np.range(3)
print (test)
print (np.exp(test)) # nth power of e
print (np.sqrt(test)) # open root
# Output [0 1 2]
	[1. 2.71828183 7.3890561]
	[0 1. 1.41421356]

**2.10.** 切り捨て: .floor()

import numpy as np
test = np.floor(10*np.random.random((3, 4)))
print (test)
# Output [[ 3. 8. 7. 0.]
	 [ 5. 9. 8. 2.]
	 [ 3. 0. 9. 0.]]

**2.11.** 配列を平坦にする: .ravel()

# Two-dimensional n rows and n columns converted to a one-dimensional array
test.ravel()
# output array([ 3., 8., 7., 0., 5., 9., 8., 2., 3., 0., 9., 0.]) 
# The data follows above, same below

**2.12.** Matrix transpose: .

test.shape = (6, 2)
print (test)
# Output [[ 3. 8.]
 [ 7. 0.]
 [ 5. 9.]
 [ 8. 2.]
 [ 3. 0.] [ 3. 0.]
 [ 9. 0.]]
test.T # The transpose of test
# output array([ 3., 7., 5., 8., 3., 9.],
       [ 8., 0., 9., 2., 0., 0.]])

**2.13.** 行によるマトリックスステッチ： np.vstack((a, b))
列によるマトリックススプライシング：np.hstack((a, b))

import numpy as np
a = np.floor(10*np.random.random((2, 2)))
b = np.floor(10*np.random.random((2, 2)))
print (a)
print ('---')
print (b)
print ('---')
print (np.vstack((a, b))) # stitch by line, i.e. vertical stitching
print ('---')
print (np.hstack((a, b))) # stitch by column, i.e., horizontal stitching
# Output [[ 5. 3.]
 [ 8. 0.]]
---
[[ 3. 0.]
 [ 6. 3.]]
---
[[ 5. 3.]] --- [[ 5. 3.
 [ 8. 0.]
 [ 3. 0.]
 [ 6. 3.]]
---
[[ 5. 3. 3. 0.]
 [ 8. 0. 6. 3.]]

**2.14.** 列による行列の分割： np.hsplit(a, 3) および np.hsplit(a, (3, 4))

import numpy as np
a = np.floor(10*np.random.random((2, 12)))
print (a)
# Output [[ 6. 7. 5. 7. 9. 1. 2. 3. 1. 9. 5. 7.]
 [ 6. 5. 2. 0. 1. 7. 8. 2. 7. 0. 5. 9.]]
print (np.hsplit(a, 3)) # split by column, i.e., in the horizontal direction, with a as the matrix to be split and 3 as the splitting into thirds
print ('---')
print (np.hsplit(a, (3, 4))) # parameter (3, 4) is a cut in front of dimension 3, which is the fourth column, and a cut in front of dimension 4, which is the fifth column
# Output [array([ 6., 7., 5., 7.],
       [ 6., 5., 2., 0.]]), array([[ 9., 1., 2., 3,]
       [ 1., 7., 8., 2.]]), array([[ 1., 9., 5., 7,]
       [ 7., 0., 5., 9.]])]
---
[array([[ 6., 7., 5,]
       [ 6., 5., 2.]]), array([[ 7.],
       [ 0.]]), array([[ 9., 1., 2., 3., 1., 9., 5., 7,]
       [ 1., 7., 8., 2., 7., 0., 5., 9.]])]

**2.15.** 行による行列の分割： np.vsplit(a, 3) および np.vsplit(a, (3, 4))

import numpy as np
a = np.floor(10*np.random.random((12, 2)))
print (a)
# Output [[ 5. 4.]
 [ 8. 7.]
 [ 3. 1.]
 [ 6. 0.]
 [ 4. 4.]
 [ 4. 5.]
 [ 2. 4.]
 [ 7. 3.]
 [ 1. 6.]
 [ 6. 9.]
 [ 2. 1.]
 [ 3. 0.]]
print (np.vsplit(a, 3)) # split by rows, that is, split horizontally and vertically, parameter a is the matrix to be split, parameter 3 is divided into three parts
print ('---')
print (np.vsplit(a, (3, 4))) # parameter (3, 4) is cut in front of dimension 3, which is the fourth row, and cut in front of dimension 4, which is the fifth row
# Output [array([ 5., 4.],
       [ 8., 7.],
       [ 3., 1.],
       [ 6., 0.]]), array([[ 4., 4.]],
       [ 4., 5.],
       [ 2., 4.],
       [ 7., 3.]]), array([[ 1., 6.],
       [ 6., 9.],
       [ 2., 1.],
       [ 3., 0.]])]
---
[array([[ 5., 4.],
       [ 8., 7.],
       [ 3., 1.]]), array([[ 6., 0.]]), array([[ 4., 4.]],
       [ 4., 5.],
       [ 2., 4.],
       [ 7., 3.],
       [ 1., 6.],
       [ 6., 9.],
       [ 2., 1.],
       [ 3., 0.]])]

**2.16.**行列の特定の要素の検索と変更
例えば、以下のコードでは、x_dataは私のコードでは行列ですが、行列のデータには欠損値があり、それは? で表されます。 私は何らかのデータ処理を行う必要があるので、例えば、? を0に置き換える必要があります。

x_data[x_data == '?'] = 0

3. 配列の作成：.array
まず、配列を使って何かをするためには、配列を作成する必要があります。配列関数 Python のシーケンスオブジェクトを渡して配列を作成します。（c のように）多層ネストした配列を渡すと多次元配列が作成されます。

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array((5, 6, 7, 8))
c = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [7, 8, 9, 10]])
print (a)
print ('---')
print (b)
print ('---')
print (c)
# Output [1 2 3 4]
---
[5 6 7 8]
---
[[ 1 2 3 4]
 [ 4 5 6 7]
 [ 7 8 9 10]]

• でnumpyをインポートした場合 import numpy コマンドを使用した場合、配列を作成する際に a = numpy.array([1, 2, 3, 4]) という形で
• でnumpyをインポートした場合 import numpy as np コマンドを使用します。

  a = np.array([1, 2, 3, 4])
  

4. クエリデータタイプ：.dtype

# Pick up the above data
print (c.dtype)
# Output int32

データ型について：Listの要素は異なるデータ型を持つことができますが、ArrayやSeriesには同じデータ型しか格納できないため、メモリを効率的に使用でき、より効果的な運用が可能になります。

**4.1.**作成時の要素タイプの指定

import numpy as np
a = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [7, 8, 9, 10]])
b = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [7, 8, 9, 10]], dtype='str')
print (a)
print ('---')
print (b)
# Output [[ 1 2 3 4]
 [ 4 5 6 7]
 [ 7 8 9 10]]
---
[['1' '2' '3' '4']]
 ['4' '5' '6' '7']
 ['7' '8' '9' '10']]

**4.2.** データ型の変換: .astype

# Pick up the data above
b = b.astype(int)
print (b)
# Output [[ 1 2 3 4]
 [ 4 5 6 7]
 [ 7 8 9 10]]

4.3. 配列のデータ型 配列のデータ型

bool -- True , False
int -- int16 , int32 , int64
float -- float16 , float32 , float64
string -- string , unicode

5. 行列の大きさを問い合わせる： .shape

import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [7, 8, 9, 10]])
print (a.shape)
print ('---')
print (b.shape)
# Output (4,)
---
(3, 4)

(4, )shapeは、1次元の配列で4つの要素を持つものです。
(3, 4) 形状は2つの要素を持ち、3行4列の2次元配列である。

**5.1.** 配列の要素数はそのままに、配列のshapeプロパティを変更することで、配列の各軸の長さを変更します。以下の例では、配列bの形状を(4, 3)に変更しています。(3, 4) から (4, 3) に変更しても、配列は転置されず、各軸の大きさが変わるだけで、メモリ上の配列要素の位置は変わりません。

b.shape = 4, 3
print (b)
# Output [[ 1 2 3]
 [ 4 4 5]
 [ 6 7 7]
 [ 8 9 10]]

**5.2.** 軸の要素が-1の場合、軸の長さは配列の要素数から自動的に計算されます。

b.shape = 2, -1
print (b)
# Output [[ 1 2 3 4 4 5]
 [ 6 7 7 8 9 10]]

**5.3.** 配列のreshapeメソッドを用いて、元の配列の形状を維持したまま、次元を変更した新しい配列を作成することができます。

a = np.array((1, 2, 3, 4))
b = a.reshape((2, 2))
b
# Output array([[1, 2],
       [3, 4]])

6. コピー(1): =
a と b はデータ格納メモリ領域を共有しているので，どちらかの配列の要素を変更すると，同時にもう一方の配列または行列の内容も変更されます．

a[2] = 100 # Change the third element of array a to 100, and the 2, or third element, of array d is changed
b
# Output array([[1, 2],
       [100, 4]])

import numpy as np
a = np.range(12)
b = a

print (a)
print (b)
print (b is a) # Determine if b is a?
# Output [ 0 1 2 3 4 5 6 7 8 9 10 11]
	[ 0 1 2 3 4 5 6 7 8 9 10 11]
	True

b.shape = 3, 4
print (a.shape)
# Output (3, 4)

print (id(a))
print (id(b))
# Output 2239367199840
	2239367199840

# The view method creates a new array object that looks at the same data.

import numpy as np
a = np.array(12)
b = a.view() # b is a newly created array, but b and a share data

b is a # Determine if b is a?
# Output False
print (b)
# Output [ 0 1 2 3 4 5 6 7 8 9 10 11]
b.shape = 2, 6 # Change b's shape, a's shape is not affected
print (a.shape)
print (b)
# Output (12,)
[[ 0 1 2 3 4 5]
 [ 6 7 8 9 10 11]]
b[0, 4] = 1234 # change b row 1 column 5 elements to 1234, a corresponding position elements are affected
print (b)
# Output [[ 0 1 2 3 1234 5]
		 [ 6 7 8 9 10 11]]
print (a)
# Output [ [ 0 1 2 3 1234 5 6 7 8 9 10 11]

7. コピー (2) - 浅いコピー： .view()

# The copy method makes a complete copy of the array and its data.

import numpy as np
a = np.array(12)
a.shape = 3, 4
a[1, 0] = 1234

c = a.copy()
c is a
c[0, 0] = 9999 # Changing the value of the element c does not affect the elements of a
print (c)
print (a)
# Output [[9999 1 2 3]
 [1234 5 6 7]
 [ 8 9 10 11]]
[[0 1 2 3]]
 [[1234 5 6 7]]
 [ 8 9 10 11]]

8. コピー (3) - ディープコピー： .copy()

import numpy as np
a = np.array([[5, 10, 15],
       [20, 25, 30],
       [35, 40, 45]])
a.ndim
# Output 2

9. クエリディメンション：.ndim

import numpy as np
a = np.array([[5, 10, 15],
       [20, 25, 30],
       [35, 40, 45]])
a.size
# Output 9

10. 要素数を問い合わせる：.size

np.zeros((3, 4)) # Create a 0 matrix with 3 rows and 4 columns
np.zeros((3, 4), dtype=np.str) # You can specify the data type at creation time

11. 0行列の作成：.zeros

np.noes((3, 4)) # Create a 1 matrix with 3 rows and 4 columns

12. 1のマトリックスを作成：.ones

np.range(10, 30, 5) # start at 10 and go to 30, not adding 5 to create an element
# Output array([10, 15, 20, 25])
# You can change the dimensionality by modifying the shape property, see above

np.range(0, 2, 0.3) # start at 0 and go to 2, not adding 0.3 generates an element
# output array([0, 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])

np.range(12).reshape(3, 4) # from 0 every plus 1 to generate a total of 12 elements, and set the matrix size by reshape to 3 rows of 4 columns
# Output array([[0, 1, 2, 3],
             [4, 5, 6, 7],
             [8, 9, 10, 11]])

np.random.random((2, 3)) # Generate a 2-row, 3-column matrix with random values between 0 and 1

13. 区間内の等分散による行列の作成：.range

from numpy import pi
np.linspace(0, 2*pi, 100) # 0 to 2*pi, take 100 values

14. 要素数による区間値：.linspace

from numpy import pi
np.linspace(0, 2*pi, 100) # 0 to 2*pi, take 100 values

15. 配列または行列に値が存在するかどうかを判断するために == を使用します。

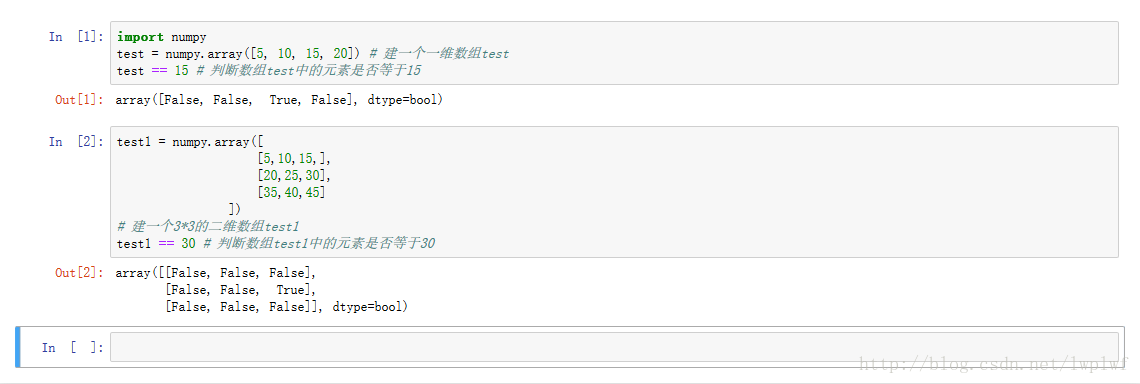
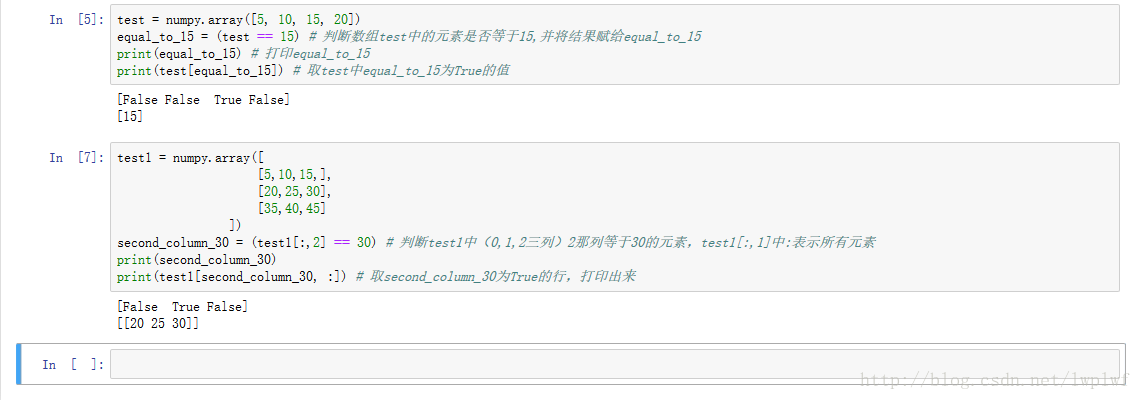
結果を変数に代入する

複数の条件を一度に判定する

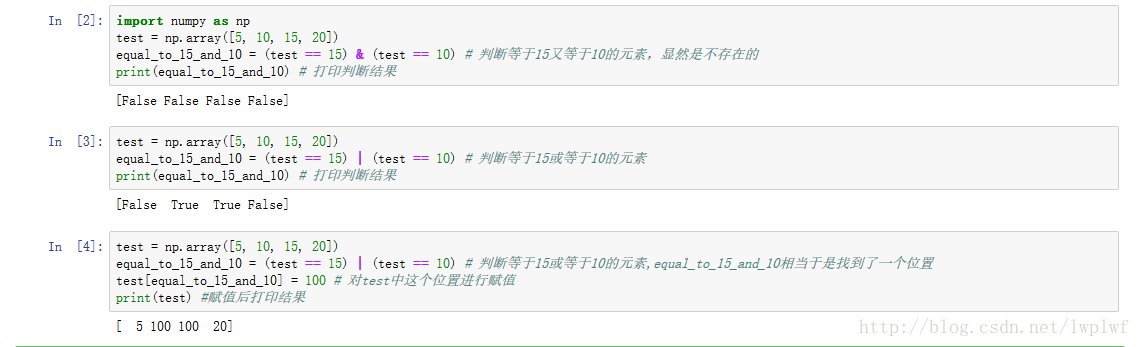
行列の場合も状況は同じです